Phân tích đa thức thành nhân tử bằng cách đặt ẩn phụ:
(x2+2x)(x2+2x+4)+3
Phân tích đa thức thành nhân tử bằng phương pháp đặt ẩn phụ
(x2+4x+8)2+3x(x2+4x+8)+2x2
\(\left(x^2+4x+8\right)^2+3x\left(x^2+4x+8\right)+2x^2=\left(x^2+4x+8+\dfrac{3}{2}x\right)^2-\dfrac{1}{4}x^2=\left(x^2+\dfrac{11}{2}x+8\right)^2-\left(\dfrac{1}{2}x\right)^2=\left(x^2+\dfrac{11}{2}x+8-\dfrac{1}{2}x\right)\left(x^2+\dfrac{11}{2}x+8+\dfrac{1}{2}x\right)=\left(x^2+5x+8\right)\left(x^2+6x+8\right)=\left(x+2\right)\left(x+4\right)\left(x^2+5x+8\right)\)
\(\left(x^2+4x+8\right)^2+3x\left(x^2+4x+8\right)+2x^2\)
\(=\left(x^2+4x+8\right)^2+x\left(x^2+4x+8\right)+2x\left(x^2+4x+8\right)+2x^2\)
\(=\left(x^2+4x+8\right)\left(x^2+5x+8\right)+2x\left(x^2+5x+8\right)\)
\(=\left(x^2+5x+8\right)\left(x+2\right)\left(x+4\right)\)
Phân tích đa thức thành nhân tử bằng phương pháp đặt ẩn phụ:
a) 36 x 6 − 24 x 3 + 4 ;
b) ( x 2 - 1 ) 2 - 18(x + l)(x -1);
c) (x + l)(x + 3)(x + 5)(x + 7) +15;
d) ( x 2 + x + 4 ) 2 + 8x( x 2 + x + 4) + 15 x 2 .
phân tích đa thức thành nhân tử bằng phương pháp đặt ẩn phụ :
\(3\left(x^2+2x\right)^2-2\left(x^2+2x\right)-1\)
Đặt x^2+2x=t =>3t^2-2t-1=3t^2-3t+t-1=3t(t-1)+(t-1)=(t-1)(3t+1)
=>(x^2+2x-1)(3x^2+6x+1)
Phân tích đa thức sau thành nhân tử :
a,x4+8x+63
b,(x5+4)+(x3+4)-16
c,(x2+2x+7)+(x2-2x+4)(x2+2x+3)
a) \(x^4+8x+63\)
\(=x^4+4x^3+9x^2-4x^3-16x^2-36x+7x^2+28x+63\)
\(=x^2\left(x^2+4x+9\right)-4x\left(x^2+4x+9\right)+7\left(x^2+4x+9\right)\)
\(=\left(x^2+4x+9\right)\left(x^2-4x+7\right)\)
c) \(\left(x^2+2x+7\right)+\left(x^2-2x+4\right)\left(x^2+2x+3\right)\left(1\right)\)
Ta có : \(x^3-8=\left(x-2\right)\left(x^2+2x+4\right)\)
\(\Rightarrow x^2+2x+4=\dfrac{x^3-8}{x-2}\)
\(\left(1\right)\Rightarrow\left[\left(\dfrac{x^3-8}{x-2}+3\right)\right]+\left(x^2-2x+4\right)\left[\left(\dfrac{x^3-8}{x-2}-1\right)\right]\)
\(=\left[\left(\dfrac{x^3-3x-14}{x-2}\right)\right]+\left(x^2-2x+4\right)\left[\left(\dfrac{x^3-2x-5}{x-2}\right)\right]\)
\(=\dfrac{1}{x-2}\left[x^3-3x-14+\left(x^2-2x+4\right)\left(x^3-2x-5\right)\right]\)
-giải phương trình
4(2x+7)-9(x+3)^2=0
- phân tích đa thức thành nhân tử bằng cách đặt ẩn phụ
(x^2+x+1)*(x^2+x+2)-12
(mọi người giải giúp mình vs ạ)
Bài 1 :
Mình nghĩ phải sửa đề ntn :
\(4\left(2x+7\right)^2-9\left(x+3\right)^2=0\)
\(\Leftrightarrow\left[2\left(2x+7\right)\right]^2-\left[3\left(x+3\right)\right]^2=0\)
\(\Leftrightarrow\left[2\left(2x+7\right)-3\left(x+3\right)\right]\left[2\left(2x+7\right)+3\left(x+3\right)\right]=0\)
\(\Leftrightarrow\left(4x+14-3x-9\right)\left(4x+14+3x+9\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(7x+23\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+5=0\\7x+23=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-5\\x=\frac{-23}{7}\end{cases}}}\)
Vậy....
b) \(A=\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)
Đặt \(q=x^2+x+1\)ta có :
\(A=q\left(q+1\right)-12\)
\(A=q^2+q-12\)
\(A=q^2+4q-3q-12\)
\(A=q\left(q+4\right)-3\left(q+4\right)\)
\(A=\left(q+4\right)\left(q-3\right)\)
Thay \(q=x^2+x+1\)ta có :
\(A=\left(x^2+x+1+4\right)\left(x^2+x+1-3\right)\)
\(A=\left(x^2+x+5\right)\left(x^2+x-2\right)\)
\(A=\left(x^2+x+5\right)\left(x^2+2x-x-2\right)\)
\(A=\left(x^2+x+5\right)\left[x\left(x+2\right)-\left(x+2\right)\right]\)
\(A=\left(x^2+x+5\right)\left(x+2\right)\left(x-1\right)\)
Cách 2 của câu 2:
Đặt \(x^2+x+2=t\)
Ta có: \(A=\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)
\(=t\left(t-1\right)-12=t^2-t-12\)
\(=\left(t-4\right)\left(t+3\right)=\left(x^2+x-2\right)\left(x^2+x+5\right)\)
\(=\left(x-1\right)\left(x+2\right)\left(x^2+x+5\right)\)
phân tích đa thức thành nhân tử (thêm bớt cùng một hạng tử):
x^3 - 2x - 4
phân tích đa thức thành nhân tử (đặt biến phụ):
x^4 + 2x^3 + 5x^2 + 4x - 12
#)Giải :
\(x^3-2x-4\)
\(=x^3+2x^2-2x^2+2x-4x-4\)
\(=x^3+2x^2+2x-2x^2-4x-4\)
\(=x\left(x^2+2x+2\right)-2\left(x^2+2x+2\right)\)
\(=\left(x-2\right)\left(x^2+2x+2\right)\)
\(x^4+2x^3+5x^2+4x-12\)
\(=x^4+x^3+6x^2+x^3+x^2+6x-2x^2-2x-12\)
\(=x^2\left(x^2+x+6\right)+x\left(x^2+x+6\right)-2\left(x^2+x+6\right)\)
\(=\left(x^2+x+6\right)\left(x^2+x-2\right)\)
\(=\left(x^2+x+6\right)\left(x-1\right)\left(x+2\right)\)
Câu 1.
Đoán được nghiệm là 2.Ta giải như sau:
\(x^3-2x-4\)
\(=x^3-2x^2+2x^2-4x+2x-4\)
\(=x^2\left(x-2\right)+2x\left(x-2\right)+2\left(x-2\right)\)
\(=\left(x-2\right)\left(x^2+2x+2\right)\)
rút gọn biểu thức
1/(2x+3)2-2(2x+3)(2x+5)+(2x+5)2
2/(x2-1)(x+2)-(x-2)(x2+2x+4)
phân tích đa thức thành nhân tử
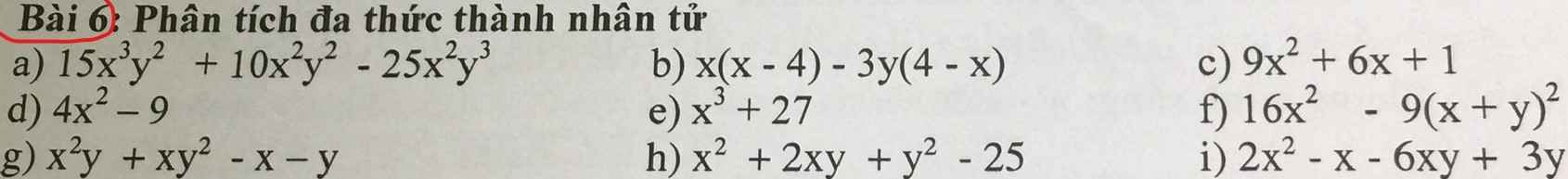
Bài 6:
c: \(9x^2+6x+1=\left(3x+1\right)^2\)
d: \(4x^2-9=\left(2x-3\right)\left(2x+3\right)\)
e: \(x^3+27=\left(x+3\right)\left(x^2-3x+9\right)\)
phân tích đa thức thành nhân tử bằng cách nhóm hạng tử
1) x2 - y2 - 2x - 2y
2) 3x2 - 3y2 - 2(x - y)2
1) \(x^2-y^2-2x-2y\)
\(=\left(x^2-y^2\right)-\left(2x+2y\right)\)
\(=\left(x+y\right)\left(x-y\right)-2\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y-2\right)\)
2) \(3x^2-3y^2-2\left(x-y\right)^2\)
\(=3\left(x^2-y^2\right)-2\left(x-y\right)^2\)
\(=3\left(x-y\right)\left(x+y\right)-2\left(x-y\right)^2\)
\(=\left(x-y\right)\left[3\left(x+y\right)-2\left(x-y\right)\right]\)
\(=\left(x-y\right)\left(3x+3y-2x+2y\right)\)
\(=\left(x-y\right)\left(x+5y\right)\)
1) x² - y² - 2x - 2y
= (x² - y²) - (2x + 2y)
= (x - y)(x + y) - 2(x + y)
= (x + y)(x - y - 2)
2) 3x² - 3y² - 2(x - y)²
= (3x² - 3y²) - 2(x - y)²
= 3(x² - y²) - 2(x - y)²
= 3(x - y)(x + y) - 2(x - y)²
= (x - y)[3(x + y) - 2(x - y)]
= (x - y)(3x + 3y - 2x + 2y)
= (x - y)(x + 5y)
`x^2-y^2 -2x-2y`
`= (x^2-y^2) -(2x+2y)`
`=(x-y)(x+y) -2(x+y)`
`= (x+y) (x-y-2)`
__
`3x^2 -3y^2 -2(x-y)^2`
`= 3(x^2 -y^2) - 2(x-y)^2`
`=3(x-y)(x+y) -2(x-y)^2`
`= (x-y) (3x+3y -2x+2y)`
`=(x-y)( x+5y)`
PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ BẰNG PHƯƠNG PHÁP ĐẶT NHÂN TỬ CHUNG
8) x2(x – 2y) + 3x(x – 2y) 9)(5x+2)(x-3)-x(x-3)
10(5x-3)(x+2)-2x(x+2)
8: \(=\left(x-2y\right)\cdot x\cdot\left(x+3\right)\)
9: \(=\left(5x+2\right)\left(x-3\right)-x\left(x-3\right)\)
\(=\left(x-3\right)\left(4x+2\right)\)
=2(2x+1)(x-3)
3: \(=2\left(x+2\right)\left(25x-15-x\right)\)
\(=2\left(x+2\right)\left(24x-15\right)\)
=6(x+2)(8x-5)