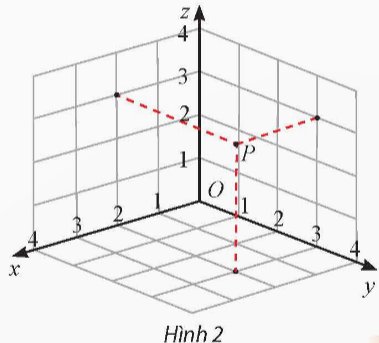
Tìm tọa độ của điểm P được biểu diễn trong Hình 2 và tính khoảng cách OP.
Cho các số phức z thỏa mãn i z + 2 - i = 0 Tính khoảng cách từ điểm biểu diễn hình học của z trên mặt phẳng tọa độ Oxy đến điểm M(3; -4)
A. 2 5
B. 13
C. 2 10
D. 2 2
Trong mặt phẳng tọa độ Oxy, cho điểm \(M({x_o};{y_o})\). Gọi P, Q tương ứng là hình chiếu vuông góc của M trên trục hoành Ox và trục tung Oy (H.4.35)
a) Trên trục Ox, điểm P biểu diễn số nào? Biểu thị \(\overrightarrow {OP} \) theo \(\overrightarrow i \) và tính độ dài của \(\overrightarrow {OP} \) theo \({x_o}\).
b) Trên trục Oy, điểm Q biểu diễn số nào? Biểu thị \(\overrightarrow {OQ} \) theo \(\overrightarrow j \) và tính độ dài của \(\overrightarrow {OQ} \) theo \({y_o}\).
c) Dựa vào hình chữ nhật OPMQ, tính độ dài của \(\overrightarrow {OM} \) theo \({x_o},{y_o}.\)
d) Biểu thị \(\overrightarrow {OM} \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \).
a) Vì P là hình chiếu vuông góc của M trên Ox nên điểm P biểu diễn hoành độ của điểm M là số \({x_o}\)
Ta có: vectơ \(\overrightarrow {OP} \) cùng phương, cùng hướng với \(\overrightarrow i \) và \(\left| {\overrightarrow {OP} } \right| = {x_o} = {x_o}.\left| {\overrightarrow i } \right|\)
\( \Rightarrow \overrightarrow {OP} = {x_o}.\;\overrightarrow i \).
b) Vì Q là hình chiếu vuông góc của M trên Oy nên điểm Q biểu diễn tung độ của điểm M là số \({y_o}\)
Ta có: vectơ \(\overrightarrow {OQ} \) cùng phương, cùng hướng với \(\overrightarrow j \) và \(\left| {\overrightarrow {OQ} } \right| = {y_o} = {y_o}.\left| {\overrightarrow j } \right|\)
\( \Rightarrow \overrightarrow {OQ} = {y_o}.\;\overrightarrow j \).
c) Ta có: \(\overrightarrow {OM} = OM\).
Mà \(O{M^2} = O{P^2} + M{P^2} = O{P^2} + O{Q^2} = {x_o}^2 + {y_o}^2\)
\( \Rightarrow \left| {\overrightarrow {OM} } \right| = \sqrt {{x_o}^2 + {y_o}^2} \)
d) Ta có: Tứ giác OPMQ là hình chữ nhật, cũng là hình bình hành nên \(\overrightarrow {OM} = \overrightarrow {OP} + \overrightarrow {OQ} \)
\( \Rightarrow \overrightarrow {OM} = {x_o}.\;\overrightarrow i + {y_o}.\;\overrightarrow j \)
Gọi P là điểm biểu diễn của số phức a+bi trong mặt
phẳng phức.Cho các mệnh đề sau:
(1) Môđun của a+bi là bình phương khoảng cách
OP.
(2) Nếu P là biểu diễn của số 3+4i thì khoảng cách
từ O đến P bằng 7.
Chọn đáp án đúng:
A. Chỉ có (1) đúng
B. Chỉ có (2) đúng
C. Cả hai đều đúng
D. Cả hai đều sai.
Gọi P là điểm biểu diễn của số phức a+bi trong mặt phẳng phức.
Cho các mệnh đề sau:
(1) Môđun của a+bi là bình phương khoảng cách OP.
(2) Nếu P là biểu diễn của số 3+4i thì khoảng cách từ O đến P bằng 7.
Chọn đáp án đúng:
A. Chỉ có (1) đúng
B. Chỉ có (2) đúng
C. Cả hai đều đúng
D. Cả hai đều sai
Chọn D.
Phải sửa lại:
Môdun của a+bi là khoảng cách OP
Nếu P là biểu diễn của số 3+4i thì khoảng cách từ O đến P bằng 3 + 4 i = 5
Số quyển vở \(x\) đã mua và số tiền \(y\) (nghìn đồng) phải trả của ba bạn Hùng, Dũng, Mạnh được biểu diễn lần lượt bởi ba điểm \(H,D,M\) trong mặt phẳng tọa độ \(Oxy\) như Hình 11.
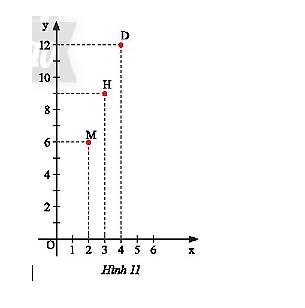
a) Tìm tọa độ của các điểm \(H,D,M\).
H(3;9); D(4;12); M(2;6)
cho đường thẳng (d) y=-4x+3
a, vẽ độ thị hàm số độ cho
b, tìm tọa độ điểm A,B của d với lận lượt vơi 2 trục tọa độ Ox và Oy
c, tính khoảng cách từ góc tọa độ đến (d )
d, tính khoảng cách từ I (-1,-2) để d
e, tính diên tích tam giác OAB
Cho số phức z = a + ( a - 3 )i với a ∈ R . Tìm a để khoảng cách từ điểm biểu diễn của số phức z đến gốc tọa độ là nhỏ nhất
A. 2 3
B. 3 2
C. 3 2
D. 2 3
Gọi M là điểm biểu diễn số phức z. Khi đó
O M = z = a 2 + a - 3 2 = 2 a - 3 2 2 + 9 2 ≥ 3 2
Dấu “=” xảy ra khi a = 3 2
Đáp án C
Cho số phức z thỏa mãn iz + 2 - i = 0. Khoảng cách từ điểm biểu diễn của z trên mặt phẳng tọa độ Oxy đến điểm M(3;-4) là:
A. 2 5
B. 13
C. 2 10
D. 2 2
Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác \(\frac{{2\pi }}{3}\) và \(\frac{\pi }{4}\) trên
đường tròn lượng giác. Xác định tọa độ của M và N trong hệ trục tọa độ Oxy .
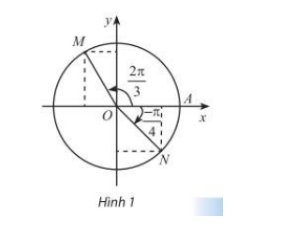
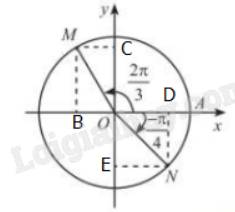
Gọi B, C lần lượt là hình chiếu của M lên Ox, Oy; D, E lần lượt là hình chiếu của N lên Ox, Oy
Ta có: OM = ON = 1
\(\widehat{MOC}=\dfrac{2\pi}{3}-\dfrac{\pi}{2}=\dfrac{\pi}{6}\\ \Rightarrow\left\{{}\begin{matrix}sin\widehat{MOC}=\dfrac{1}{2}\Rightarrow MC=\dfrac{1}{2}\\cos\widehat{MOC}=\dfrac{\sqrt{3}}{2}\Rightarrow MB=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
Do điểm M có hoành độ nằm bên trái trục Ox nên tọa độ của điểm M là \(M\left(-\dfrac{1}{2};\dfrac{\sqrt{3}}{2}\right)\)
\(\widehat{NOD}=-\dfrac{\pi}{4}\\ \Rightarrow\left\{{}\begin{matrix}sin\widehat{NOD}=-\dfrac{\sqrt{2}}{2}\Rightarrow ND=-\dfrac{\sqrt{2}}{2}\\cos\widehat{NOD}=\dfrac{\sqrt{2}}{2}\Rightarrow NE=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
Vậy tọa độ điểm N là \(N\left(\dfrac{\sqrt{2}}{2};-\dfrac{\sqrt{2}}{2}\right)\)
Đồ thị biểu diễn độ lớn lực tương tác giữa hai điện tích điểm trong chân không phụ thuộc vào khoảng cách r được cho như hình vẽ bên. Tính tỉ số F 2 F 1
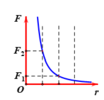
A. 2
B. 3
C. 4
D. 5