Tính bằng cách thuận tiện.
a) 524 × 63 + 524 × 37 – 2 400 b) \(\dfrac{7}{9}\times\dfrac{6}{5}+\dfrac{6}{5}\times\dfrac{2}{9}+\dfrac{4}{5}\)
Tính bằng cách thuận tiện.
a) \(\dfrac{2}{13}\times\dfrac{22}{5}\times\dfrac{13}{2}\) b) \(\dfrac{3}{5}\times\dfrac{6}{7}+\dfrac{6}{7}\times\dfrac{3}{5}\)
\(a,\dfrac{2}{13}\times\dfrac{22}{5}\times\dfrac{13}{2}\\ =\left(\dfrac{2}{13}\times\dfrac{13}{2}\right)\times\dfrac{22}{5}\\ =1\times\dfrac{22}{5}=\dfrac{22}{5}\\ b,\dfrac{3}{5}\times\dfrac{6}{7}+\dfrac{6}{7}\times\dfrac{3}{5}\\ =\dfrac{3}{5}\times\left(\dfrac{6}{7}+\dfrac{6}{7}\right)\\ =\dfrac{3}{5}\times\dfrac{12}{7}=\dfrac{36}{35}\)
\(a,=\left(\dfrac{2}{13}\times\dfrac{13}{2}\right)\times\dfrac{22}{5}=\dfrac{22}{5}\\ b,=\dfrac{3}{5}\times\left(\dfrac{6}{7}+\dfrac{6}{7}\right)\\ =\dfrac{3}{5}\times\dfrac{12}{7}\\ =\dfrac{36}{35}\)
Tính bằng cách thuận tiện.
a) \(\dfrac{3}{5}\times\dfrac{17}{21}+\dfrac{2}{5}\times\dfrac{17}{21}\) b) \(\dfrac{11}{19}\times\dfrac{2}{7}+\dfrac{5}{7}\times\dfrac{11}{19}\)
a) \(\dfrac{3}{5}\times\dfrac{17}{21}+\dfrac{2}{5}\times\dfrac{17}{21}\)
\(=\dfrac{17}{21}\times\left(\dfrac{3}{5}+\dfrac{2}{5}\right)\)
\(=\dfrac{17}{21}\times1\)
\(=\dfrac{17}{21}\)
b) \(\dfrac{11}{19}\times\dfrac{2}{7}+\dfrac{5}{7}\times\dfrac{11}{19}\)
\(=\dfrac{11}{19}\times\left(\dfrac{2}{7}+\dfrac{5}{7}\right)\)
\(=\dfrac{11}{19}\times1\)
\(=\dfrac{11}{19}\)
a: =17/21(3/5+2/5)
=17/21*5/5
=17/21
b: =11/19(2/7+5/7)
=11/19*1
=11/19
Tính bằng cách thuận tiện.
a) \(\dfrac{3}{5}\times\dfrac{7}{11}\times\dfrac{5}{3}\times11\)
b) \(\dfrac{3}{8}\times\dfrac{2}{7}+\dfrac{5}{7}\times\dfrac{3}{8}\)
a)
\(\dfrac{3}{5}\times\dfrac{7}{11}\times\dfrac{5}{3}\times11\\ =\left(\dfrac{3}{5}\times\dfrac{5}{3}\right)\times\left(\dfrac{7}{11}\times11\right)\\ =\dfrac{3\times5}{5\times3}\times\dfrac{7\times11}{11}\\ =1\times7\\ =7\)
b)
\(\dfrac{3}{8}\times\dfrac{2}{7}+\dfrac{5}{7}\times\dfrac{3}{8}\\ =\dfrac{3}{8}\times\left(\dfrac{2}{7}+\dfrac{5}{7}\right)\\ =\dfrac{3}{8}\times\dfrac{7}{7}\\ =\dfrac{3}{8}\times1=\dfrac{3}{8}\)
Tính:
a) \(\dfrac{9}{5}+\dfrac{2}{5}\times\dfrac{4}{6}\)
b) \(\dfrac{3}{8}\times2-\dfrac{6}{7}\times\dfrac{1}{3}\)
Tính bằng cách thuận tiện nhất:
a)\(\dfrac{1}{5}+\dfrac{5}{9}+\dfrac{4}{5}+\dfrac{1}{9}+\dfrac{3}{9}\)
b)\(\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{4}{3}+\dfrac{2}{6}+\dfrac{2}{3}+\dfrac{5}{6}\)
giải giúp mình với !
a, \(=\dfrac{1+4}{5}+\dfrac{5+1+3}{9}=1+1=2\)
b, \(=\dfrac{1+4+2}{3}+\dfrac{1+2+5}{6}=\dfrac{6}{3}+\dfrac{8}{6}=2+\dfrac{4}{3}=\dfrac{6+4}{3}=\dfrac{10}{3}\)
Tính (theo mẫu):
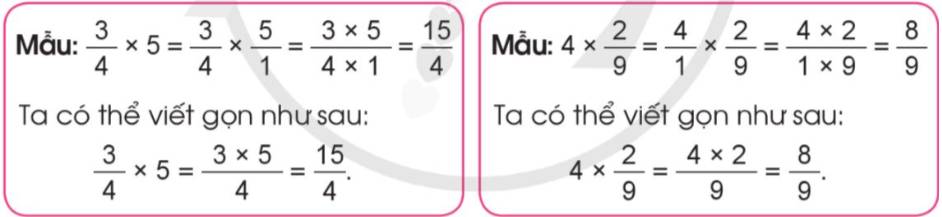
a) \(\dfrac{5}{6}\times7\) b) \(\dfrac{7}{10}\times3\) c) \(5\times\dfrac{4}{21}\) d) \(2\times\dfrac{5}{9}\)
a: \(\dfrac{5}{6}\cdot7=\dfrac{5\cdot7}{6}=\dfrac{35}{6}\)
b: \(\dfrac{7}{10}\cdot3=\dfrac{7\cdot3}{10}=\dfrac{21}{10}\)
c: \(5\cdot\dfrac{4}{21}=\dfrac{5\cdot4}{21}=\dfrac{20}{21}\)
d: \(2\cdot\dfrac{5}{9}=\dfrac{2\cdot5}{9}=\dfrac{10}{9}\)
Bài 1: Tính
a) \(\dfrac{9}{5}+\dfrac{2}{5}\) x \(\dfrac{4}{6}\) b) \(\dfrac{3}{8}\) x 2 - \(\dfrac{6}{7}\) x \(\dfrac{1}{3}\)
Bài 2: Tính bằng cách thuận tiện nhất:
a) \(\dfrac{11}{23}+\dfrac{2}{23}+\dfrac{9}{23}+\dfrac{18}{23}\) b)\(\dfrac{25}{12}+\dfrac{17}{6}-\dfrac{15}{36}-\dfrac{15}{6}\)
Bài 3: Một hình chữ nhật có chiều rộng là \(\dfrac{3}{5}\) m và bằng một nửa chiều dài. Tính diện tích hình chữ nhật đó.
Tính:
a) \(\dfrac{2}{5}\times\dfrac{3}{8}\times\dfrac{3}{4}\) b) \(\dfrac{1}{3}\times\dfrac{1}{6}\times\dfrac{1}{9}\)
c) \(\dfrac{3}{4}:\dfrac{1}{5}:\dfrac{7}{8}\) d) \(\dfrac{3}{5}:\dfrac{1}{5}:\dfrac{1}{8}\)
a) $\frac{2}{5} \times \frac{3}{8} \times \frac{3}{4} = \frac{{2 \times 3 \times 3}}{{5 \times 8 \times 4}} = \frac{{18}}{{160}} = \frac{9}{{80}}$
b) $\frac{1}{3} \times \frac{1}{6} \times \frac{1}{9} = \frac{{1 \times 1 \times 1}}{{3 \times 6 \times 9}} = \frac{1}{{162}}$
c) $\frac{3}{4}:\frac{1}{5}:\frac{7}{8} = \frac{3}{4} \times \frac{5}{1} \times \frac{8}{7} = \frac{{3 \times 5 \times 8}}{{4 \times 1 \times 7}} = \frac{{120}}{{28}} = \frac{{30}}{7}$
d) $\frac{3}{5}:\frac{1}{5}:\frac{3}{8} = \frac{3}{5} \times \frac{5}{1} \times \frac{8}{3} = \frac{{3 \times 5 \times 8}}{{5 \times 1 \times 3}} = 8$
Tính bằng cách thuận tiện nhất:
a) 60 x (\(\dfrac{7}{12}\) + \(\dfrac{4}{15}\))
b) \(\dfrac{1}{2}\) x \(\dfrac{2}{3}\) x \(\dfrac{3}{4}\) x \(\dfrac{4}{5}\) x \(\dfrac{5}{6}\) x \(\dfrac{6}{7}\) x \(\dfrac{7}{8}\) x \(\dfrac{8}{9}\)
60x [7/12+4/15]
60x153/180
=9180/180
b 1/2x2/3x3/4x4/5x5/6x6/7x7/8x8/9=40320/4032
bài 3: tính bằng cách thuận tiện
a) \(\dfrac{13}{50}\) + 0,09 + \(\dfrac{41}{100}\) + 0,24 b) \(9\dfrac{1}{4}\) + \(6\dfrac{2}{7}\) + \(7\dfrac{3}{5}\) + \(8\dfrac{2}{3}\) + \(\dfrac{2}{5}\) + \(\dfrac{1}{3}\) + \(\dfrac{5}{7}\) + \(\dfrac{3}{4}\)
Bài 4: so sánh các cặp phân số sau:
a) \(\dfrac{2008}{2009}\) và \(\dfrac{10}{9}\) b) \(\dfrac{1}{a-1}\) và \(\dfrac{1}{a+1}\) (a>1)
Bài 5: cho phân số \(\dfrac{15}{39}\). Tìm 1 số tự nhiên, biết rằng khi thêm số đó vào mẫu số của phân số đã cho và giữ nguyên tử số thì được phân số mới bằng \(\dfrac{3}{11}\)
giải giúp mik vs, mik cần gấp!
Bài 3
a,26/100+0,009+41/100+0,24
0,26+0,09+0,41+0,24
(0,26+0,24)+(0,09+0,41)
0,5+0,5
=1
b,9+1/4+6+2/7+7+3/5+8+2/3+2/5+1/3+5/7+3/4
(9+6+7+8)+(2/7+5/7)+(1/4+3/4)+(3/5+2/5)+(2/3+1/3)
30+1+1+1+1
=34
Bài 4,5 khó quá mik ko bít lamf^^))
Bài 5: vì \(\dfrac{3}{11}\) = \(\dfrac{3\times5}{11\times5}\) = \(\dfrac{15}{55}\)
Vậy Khi giữ nguyên tử số thì số cần thêm vào mẫu số là:
55 - 39 = 16
Đáp số: 16
Bài 4: a, \(\dfrac{2008}{2009}\) < 1; \(\dfrac{10}{9}\) > 1
\(\dfrac{2008}{2009}\) < \(\dfrac{10}{9}\)
b, \(\dfrac{1}{a+1}\) và \(\dfrac{1}{a-1}\)
Ta có: a + 1 > a - 1 ⇒ \(\dfrac{1}{a+1}\) < \(\dfrac{1}{a-1}\)