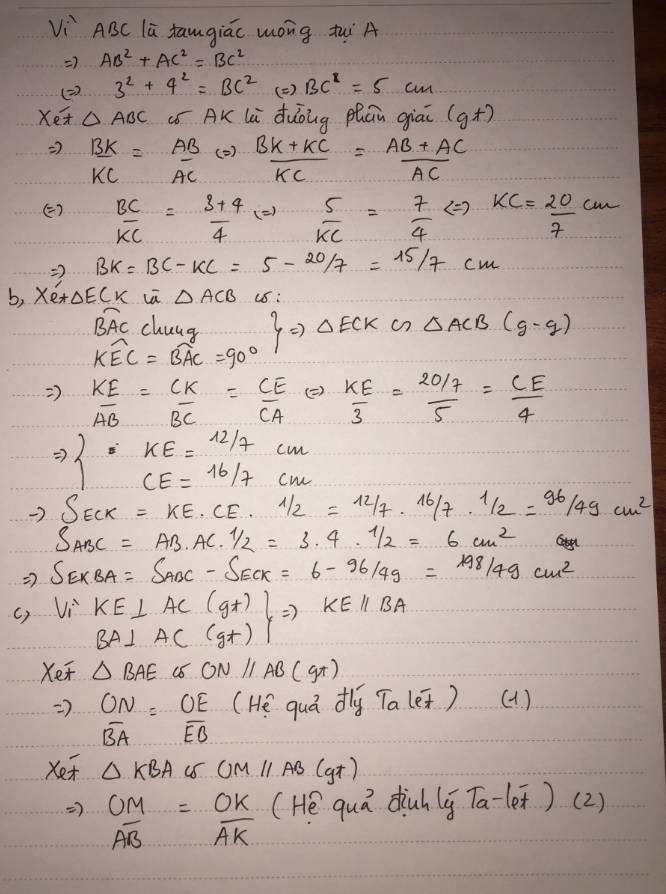Cho tam giác ABC vuông tại A có CK là phân giác trong .Biết AC= 4cm, BC= 5cm.Tính KA,KB,KC

Những câu hỏi liên quan
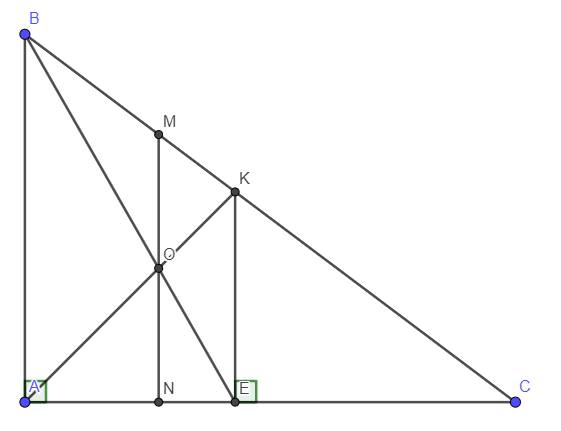
cho tam giác ABC vuông tại A có AB=3cm, AC=4cm, AK là tia phân giác của BAC (K thuộc BC)
a, Tính tỉ số KB/KC và độ dài các đoạn thẳng BC, KB, KC?
b, Từ K kẻ KE vuông góc với AC tại E ( E thuộc AC). Tính độ dài KE, AE và diệntích tứ giác AEKB?
c, Gọi O là giao điểm của AK và BE. Qua O kẻ đường thẳng song song với AB, cắt BC và AC lần lượt tại M và N. Cm rằng OM=ON
giúp mik vs
B1: Cho tam giác ABC có AB bằng 10cm, AC bằng 8cm, BC = 6cm đường cao CK
a) Chứng minh tam giác ABC vuông tại C
b tính CK, KA, KB
Cho tam giác ABC vuông tại C ( AC<AB). Trên AB lấy điểm D sao cho AC= AD. Tia phân giác của góc A cắt BC tại K
a. Chứng minh rằng KD vuông góc với AB
b. So sánh KC; KB
a: Xét ΔACK và ΔADK co
AC=AD
góc CAK=góc DAK
AK chung
=>ΔACK=ΔADK
=>góc ADK=90 độ
=>KD vuông góc AB
b: Xét ΔACB có AK là phân giác
nên KC/AC=KB/AB
mà AC<AB
nên KC<KB
Đúng 1
Bình luận (0)
ai biết giải giúp minh với:Câu 1:Cho tam giác ABC có 3 góc nhọn,các đường cao AD,BE,CK cắt nhau tại H.chứng minha,tứ giác HECD nội tiếpb,Tia DA là tia phân giác góc EDK Cây 2:cho tam giác ABC vuông tai A,biết ab6cm,ac8cmA.tính bcB,kẻ đường cao AH,tính Ah Câu 3:Cho tam giác abc vuông tại A,BIẾT AC4cm,Bc5cm.A,Tính cạnh ABB,kẻ đường cao AH,TÍNH AHCâu 4:Cho tam giác vuông ABC,vuông tại A(H thuộc BC).bIẾT AB12CM,AC5CM.tính BH,CHCâu 5:cho tam giác ABC vuông tại A,đường cao AH(H THUỘC BC).biết BC18cm,B...
Đọc tiếp
ai biết giải giúp minh với:
Câu 1:Cho tam giác ABC có 3 góc nhọn,các đường cao AD,BE,CK cắt nhau tại H.chứng minh
a,tứ giác HECD nội tiếp
b,Tia DA là tia phân giác góc EDK
Cây 2:cho tam giác ABC vuông tai A,biết ab=6cm,ac=8cm
A.tính bc
B,kẻ đường cao AH,tính Ah
Câu 3:Cho tam giác abc vuông tại A,BIẾT AC=4cm,Bc=5cm.
A,Tính cạnh AB
B,kẻ đường cao AH,TÍNH AH
Câu 4:Cho tam giác vuông ABC,vuông tại A(H thuộc BC).bIẾT AB=12CM,AC=5CM.tính BH,CH
Câu 5:cho tam giác ABC vuông tại A,đường cao AH(H THUỘC BC).biết BC=18cm,BH=6cm.Tính độ dài các cạnh AB,AC
Cau 6:Cho tam giác ABC,vuông tại A,biết AB=4cm,đường cao AH=2CM,tính các góc và các cạnh còn lại cua tam giac.?
bạn hỏi nhiều quá , các bạn nhìn vào ko biết trả lời sao đâu !!!
Đúng 1
Bình luận (0)
rối mắt quá mà viết dày nên bài nọ xọ bài kia mình ko trả lời được cho dù biết rất rõ
Đúng 0
Bình luận (0)
cho tam giác abc có bc = 3cm, ac = 4cm, ab =5cm đường cao ck
1) chứng minh tam giác abc vuông
2) tính CK, BK, KA
1: Xét ΔABC có \(CA^2+CB^2=AB^2\)
nên ΔCAB vuông tại C
2: Xét ΔCAB vuông tại C có CK là đường cao
nên \(CK\cdot AB=CA\cdot CB\)
=>\(CK\cdot5=3\cdot4=12\)
=>CK=2,4(cm)
Xét ΔCAB vuông tại C có CK là đường cao
nên \(\left\{{}\begin{matrix}CA^2=AK\cdot AB\\CB^2=BK\cdot BA\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AK=\dfrac{4^2}{5}=3,2\left(cm\right)\\BK=\dfrac{3^2}{5}=1,8\left(cm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A. các đường phân giác của góc B và góc C cắt nhau tại K. Biết hình chiếu của KB và KC trên trên BC có độ dai lần lượt là 4cm và 9cm. Tính diện tích ABC
câu 1:Cho tam giác ABC,vuông tại A,đường cáo AH(H thuộc BC).Biết AB12CM,Ac5cm.tính BH,CHCâu 2:cho tam giác ABC vuông tại A,đường cáo AH(H thuộc BC).Biết AB18cm,BH6cm.tính đô dài các cạnh AB,ACCâu 3:cho tam giac abc vuông tại a,biết ab-3cm,ac4cm,a.tinh bcb:kẻ đường cao ah,tính bhCâu 4:cho tam giác ABC Vuông tại A,biết ab4cm,đường cao ah2cm.Tính các góc và các cạnh còn lại của tam giác
Đọc tiếp
câu 1:Cho tam giác ABC,vuông tại A,đường cáo AH(H thuộc BC).Biết AB=12CM,Ac=5cm.tính BH,CH
Câu 2:cho tam giác ABC vuông tại A,đường cáo AH(H thuộc BC).Biết AB=18cm,BH=6cm.tính đô dài các cạnh AB,AC
Câu 3:cho tam giac abc vuông tại a,biết ab-3cm,ac=4cm,
a.tinh bc
b:kẻ đường cao ah,tính bh
Câu 4:cho tam giác ABC Vuông tại A,biết ab=4cm,đường cao ah=2cm.Tính các góc và các cạnh còn lại của tam giác
Câu 1:
Áp dụng đ/lí pytago vào tam giác ABC vuông tại A CÓ:AB^2+AB^2=BC^2
Hay: 12^2+5^2=169=BC^2
=> BC=13cm
ÁP dụng hệ thức ta có:
+) AB^2=BH.BC
Hay: BH=AB^2:BC=144:13 =144/13(cm)
Ta có CH=BC-BH=13-144/13=25/13(cm)
Đúng 0
Bình luận (0)
Bạn chỉ cần áp dụng hệ thức lượng là đc rồi o0o
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , đường cao AH . Chứng minh rằng 1/AH^2=1/AB^2+1/ac^2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
: Cho tam giác ABC vuông tại C có và đường phân giác của góc BAC cắt BC tại E. Kẻ EK AB tại K(K AB). Kẻ BD vuông góc với AE ta D ( D AE). Chứng minh:
a) Tam giác ACE bằng tam giác AKE.
b) AE là đường trung trực của đoạn thẳng CK.
c) KA = KB.
d) EB > EC.
a) Xét \(\Delta ACE\) và \(\Delta AKE\) có:
\(\left\{{}\begin{matrix}\widehat{ACE}=\widehat{AKE}=90^o\\AE-\text{cạnh chung}\\\widehat{EAC}=\widehat{EAK}\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow \Delta ACE=\Delta AKE(ch-gn)\)
b) Từ câu a ta có \(\Delta ACE=\Delta AKE\) nên AC = AK, EC = EK. Suy ra AE là đường trung trực của CK.
c) Đề bài sai
d) Ta có EK = EC mà EK < EB (quan hệ giữa đường vuông góc và đường xiên) nên EB > EC.
Đúng 3
Bình luận (0)
Cho tam giác ABC vuông tại A có. Vẽ AK vuông góc BC ( K thuộc BC). Trên tia đối của tia KA lấy điểm M sao cho KA = KM
a,Chứng minh : tam giác KAB = tam giác KMB. Tính số đo góc MAB
b,Trên tia KB lấy điểm D sao cho KD = KC. Tia MD cắt AB tại N. Chứng minh : MN vuông góc AB
c,So sánh MD + DB với AB
a: Xét ΔKAB vuông tại K và ΔKMB vuông tại K có
KA=KM
KB chung
Do đó: ΔKAB=ΔKMB
b: Xét tứ giác ACMD có
K là trung điểm chung của AM và CD
=>ACMD là hình bình hành
=>MD//AC
=>MN//AC
Ta có: MN//AC
AB\(\perp\)AC
Do đó: MN\(\perp\)AB
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC tại D . Vẽ DE vuông góc với BC . Đường thẳng DE cắt AB tại K
a) chứng minh tam giác BAD= tam giác BED
b) chứng minh tam giác ADK = tam giác EDC
c) chứng minh AE//KC
d) Cho AB=3 ; BC=5 . Tính KC
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
b: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó: ΔADK=ΔEDC
c: Xét ΔBKC có BA/AK=BE/EC
nên AE//KC
Đúng 1
Bình luận (0)