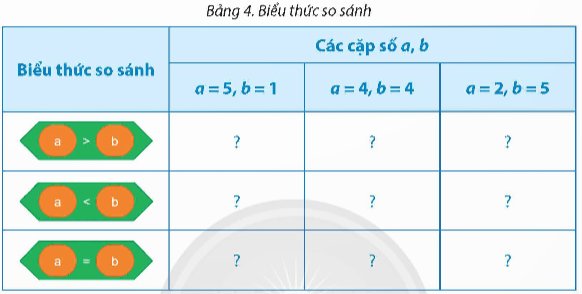
Trong Bảng 4, em hãy cho biết kết quả của mỗi biểu thức so sánh đối với từng cặp số a, b.
Cho biết khối lượng từng loại nu của 1 cặp NST (đvị tính: 108 đvc) ghi trong bảng 1. Các cặp NST (I, II, III, IV) trong bảng 2 là kết quả của đột biến từ NST đã cho.
Bảng 1

Bảng 2
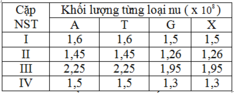
Hãy xác định tổ hợp các đột biến nào phù hợp với số liệu trong bảng 2 theo trình tự NST : I – II – III - IV.
A. lặp đoạn – ba nhiễm – mất đoạn – đảo đoạn.
B. lặp đoạn – mất đoạn – ba nhiễm–đảo đoạn.
C. ba nhiễm– mất đoạn – lặp đoạn – đảo đoạn.
D. mất đoạn – đảo đoạn– ba nhiễm– lặp đoạn.
I. G- X tăng / A –T giữ nguyên => Đột biến lặp đoạn
II. A-T giảm/ G-X giữ nguyên => Đột biến mất đoạn
III. Tất cả các loại nucleotit tăng 1.5 lần => đột biến thể 3 nhiễm
IV . Tất cả các loại nucleotit giữ nguyên => Đột biến đảo đoạn
Đáp án B
Câu lạc bộ học tiếng Nhật của trường THCS Đoàn Kết thống kê số học viên trong 4 năm liên tiếp trong bảng sau:
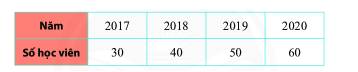
a) Hãy vẽ biểu đồ cột biểu diễn số liệu ở bảng trên.
b) Số lượng học viên tăng theo từng năm là bao nhiêu?
c) So sánh số học viên năm 2020 và năm 2017.
a)
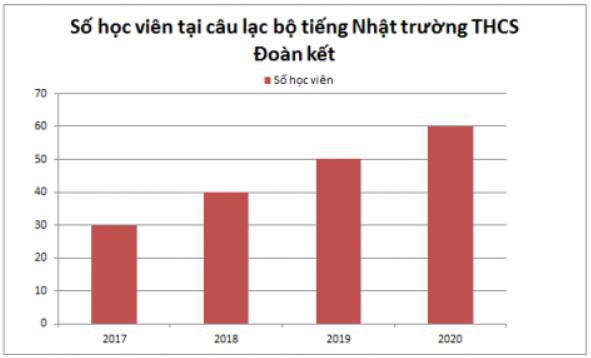
b) Số lượng học sinh tăng theo từng năm là 10 học sinh.
c) Học viên năm 2020 gấp 2 lần học viên năm 2017
cho biểu thức so sánh: 16 div 5 <> 3;
hãy cho biết kết quả của phép tính trên
A.3 = 3 B. 1 < 3
C. Sai D. Đúng
a) Trong bảng thống kê sau:
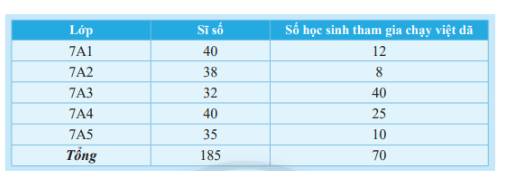
Hãy so sánh số học sinh tham gia chạy việt dã của mỗi lớp với sĩ số của lớp đó để tìm điểm chưa hợp lí của bảng thống kê trên.
b) Nêu nhận xét của em về các tỉ lệ phần trăm trong bảng thống kê sau:

c) Kết quả tìm hiểu về sở thích đối với môn bóng đá của tất cả học sinh lớp 7A được cho bởi bảng thống kê sau:

a) Số học sinh tham gia chạy việt dã của lớp 7A3 lớn hơn sĩ số lớp 7A3 nên dữ liệu này là chưa hợp lí.
b) Các tỉ lệ phần trăm không hợp lí vì tổng tỉ lệ phần trăm của tất cả các thành phần phải bằng 100%
c) Dữ liệu trên không đại diện cho sở thích đối với môn bóng đá của tất cả học sinh lớp 7A vì ta chưa biết sở thích của các bạn nữ trong lớp
Bảng 3.4 thể hiện kết quả đo khối lượng của một túi trái cây bằng cân đồng hồ. Em hãy xác định sai số tuyệt đối ứng với từng lần đo, sai số tương đối của phép đo. Biết sai số dụng cụ là 0,1 kg.
Sai số tuyệt đối của phép đo:
Sai số tương đối của phép đo:
Kết quả phép đo:
Bảng 3.4 thể hiện kết quả đo khối lượng của một túi trái cây bằng cân đồng hồ. Em hãy xác định sai số tuyệt đối ứng với từng lần đo, sai số tương đối của phép đo. Biết sai số dụng cụ là 0,1 kg.
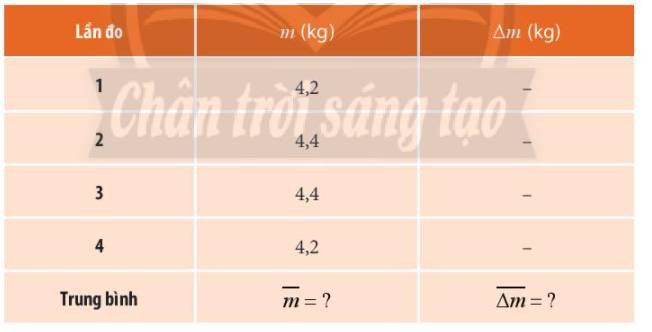
Sai số tuyệt đối của phép đo: \(\Delta m = \overline {\Delta m} + \Delta {m_{dc}} = ?\)
Sai số tương đối của phép đo: \(\delta m = \frac{{\Delta m}}{{\overline m }}.100\% = ?\)
Kết quả phép đo: \(m = \overline m \pm \Delta m = ?\)
Giá trị trung bình khối lượng của túi trái cây là:
\(\overline m = \frac{{{m_1} + {m_2} + {m_3} + {m_4}}}{4} = \frac{{4,2 + 4,4 + 4,4 + 4,2}}{4} = 4,3(kg)\)
Sai số tuyệt đối ứng với mỗi lần đo là:
\(\begin{array}{l}\Delta {m_1} = \left| {\overline m - {m_1}} \right| = \left| {4,3 - 4,2} \right| = 0,1(kg)\\\Delta {m_2} = \left| {\overline m - {m_2}} \right| = \left| {4,3 - 4,4} \right| = 0,1(kg)\\\Delta {m_3} = \left| {\overline m - {m_3}} \right| = \left| {4,3 - 4,4} \right| = 0,1(kg)\\\Delta {m_4} = \left| {\overline m - {m_4}} \right| = \left| {4,3 - 4,2} \right| = 0,1(kg)\end{array}\)
Sai số tuyệt đối trung bình của phép đo:
\(\overline {\Delta m} = \frac{{\Delta {m_1} + \Delta {m_2} + \Delta {m_3} + \Delta {m_4}}}{4} = \frac{{0,1 + 0,1 + 0,1 + 0,1}}{4} = 0,1(kg)\)
Sai số tuyệt đối của phép đo là:
\(\Delta m = \overline {\Delta m} + \Delta {m_{dc}} = 0,1 + 0,1 = 0,2(kg)\)
Sai số tương đối của phép đo là:
\(\delta m = \frac{{\Delta m}}{{\overline m }}.100\% = \frac{{0,2}}{{4,2}}.100\% = 4,65\% \)
Kết quả phép đo:
\(m = \overline m \pm \Delta m = 4,3 \pm 0,2(kg)\)
Trong bảng sau, tổng ba số của mỗi hàng ngang, mỗi hàng dọc và mỗi đường chéo bằng nhau. Hãy tính giá trị của biểu thức: ( B x1,5 - C : D ) x A
Trả lời: Giá trị của biểu thức là
(Nhập kết quả là số thập phân gọn nhất)
a) Tính và so sánh giá trị hai biểu thức sau: 5 x (4 + 3) và 5 x 4 + 5 x 3.
b) Thảo luận nội dung sau và lấy ví dụ minh hoạ:
Khi nhân một số một số với một tổng, ta có thể nhân số đó với từng số hạng của tổng , rồi cộng kết quả với nhau
Khi nhân một tổng với một số, ta có thể nhân từng số hạng của toonge với số đó , rồi cộng các kết quả với nhau
c) Tính:
32 x (200 + 3)
(125 + 9) x 8
a)
5 × (4 + 3) = 5 × 7 = 35
5 × 4 + 5 × 3 = 20 + 15 = 35
Vậy 5 × (4 + 3) = 5 × 4 + 5 × 3.
b)
- Khi nhân một số với một tổng, ta có thể nhân số đó với từng số hạng của tổng, rồi cộng các kết quả với nhau.
VD: 3 × (2 + 9) = 3 × 2 + 3 × 9 = 6 + 27 = 33
- Khi nhân một tổng với một số ta có thể nhân từng số hạng của tổng với số đó rồi cộng các kết quả với nhau.
(4 + 5) × 6 = 4 × 6 + 5 × 6 = 24 + 30 = 54
c) Tính:
32 × (200 + 3) = 32 × 200 + 32 × 3 = 6 400 + 96 = 6 496
(125 + 9) × 8 = 125 × 8 + 9 × 8 = 1 000 + 72 = 1 072
So sánh thời gian hoàn thành cuộc thi của từng học sinh, hãy ghi kết quả xếp hạng theo mẫu Bảng 8.1.
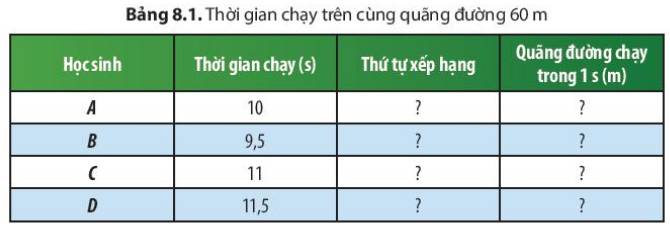
Bảng 8.1: Thời gian chạy trên cùng quãng đường 60 m
Học sinh | Thời gian chạy bộ (s) | Thứ tự xếp hạng |
A | 10 | 2 |
B | 9,5 | 1 |
C | 11 | 3 |
D | 11,5 | 4 |
Có 3 bình, mỗi bình chứa 1 trong các khí sau: metan, axetilen, khí cacbonic. Đánh số A, B, C vào các bình này và tiến hành các thí nghiệm với từng chất khí. Kết quả thí nghiệm được ghi ở bảng sau:

Hãy cho biết 3 bình A, B, C chứa lần lượt những khí nào?
A. Bình A chứa axetilen, bình B chứa metan, bình C chứa cacbonic.
B. Bình A chứa metan, bình B chứa axetilen, bình C chứa cacbonic.
C. Bình A chứa axetilen, bình B chứa cacbonic, bình C chứa metan.
D. Bình A chứa cacbonic, bình B chứa metan, bình C chứa axetilen.
Khí làm mất màu dung dịch brom là axetilen => Bình B chứa axetilen
Khí làm vẩn đục nước vôi trong là cacbonic => Bình C chứa cacbonic
Khí không phản ứng với cả 2 chất là metan => Bình A chứa metan
Đáp án: B