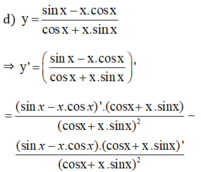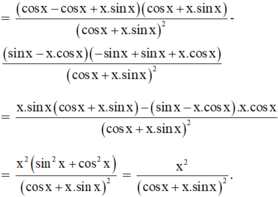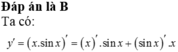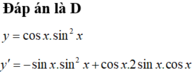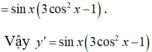Ta có:   y ' = 2 x . sin x + ​   x 2 . cos x

y ' ' = ​​ 2 sin x + 2 x . c osx +​   2x.cosx -   ​x 2 s inx           = ( 2 − x 2 ) sin x + 4 x . cos x

Chọn đáp án C

a) ĐK:  \(\cos x\ne0\)( vì tan x = sinx/cosx nên cos x khác 0)

<=> \(x\ne\frac{\pi}{2}+k\pi\); k thuộc Z

TXĐ: \(ℝ\backslash\left\{\frac{\pi}{2}+k\pi\right\}\); k thuộc Z

b) ĐK: \(1+\cos2x\ne0\Leftrightarrow\cos2x\ne-1\Leftrightarrow2x\ne\pi+k2\pi\Leftrightarrow x\ne\frac{\pi}{2}+k\pi\); k thuộc Z

=> TXĐ: \(ℝ\backslash\left\{\frac{\pi}{2}+k\pi\right\}\); k thuộc Z

c) ĐK: \(\hept{\begin{cases}\cot x-\sqrt{3}\ne0\\\sin x\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ne\frac{\pi}{6}+k\pi\text{​​}\text{​​}\\x\ne l\pi\end{cases}}\); k,l thuộc Z

=>TXĐ: ....

d) ĐK: \(1-2\sin^2x\ne0\Leftrightarrow\cos2x\ne0\Leftrightarrow2x\ne\frac{\pi}{2}+k\pi\Leftrightarrow x\ne\frac{\pi}{4}+\frac{k\pi}{2}\)

=> TXĐ:...

1/ \(y'=\left(1-3x\right)'\sqrt{x-3}+\left(1-3x\right)\left(\sqrt{x-3}\right)'=-3\sqrt{x-3}+\dfrac{1}{2\sqrt{x-3}}\left(1-3x\right)\)

2/ \(y'=\dfrac{1}{\sqrt{2x+1}}-\dfrac{1}{\left(x+1\right)^2}\)

3/ \(y'=\dfrac{1}{2}.\sqrt{\dfrac{1+x}{1-x}}.\left(\dfrac{1-x}{1+x}\right)'=\dfrac{1}{2}\sqrt{\dfrac{1+x}{1-x}}.\dfrac{-2}{\left(1+x\right)^2}=-\sqrt{\dfrac{1+x}{1-x}}.\dfrac{1}{\left(1+x\right)^2}\)

4/ \(y'=\left(\cos5x\right)'.\cos7x+\cos5x.\left(\cos7x\right)'=-5\sin5x.\cos7x-7\cos5x\sin7x\)

5/ \(y'=\left(\cos x\right)'\sin^2x+\cos x\left(\sin^2x\right)'=-\sin^3x+2\sin x.\cos^2x\)

6/ \(y'=\left(\tan^42x\right)'=4.\tan^32x.\dfrac{2}{\cos^22x}\)

7/ \(y'=\dfrac{2\sin x+2\cos x-2x.\cos x+2x\sin x}{\left(\sin x+\cos x\right)^2}\)

Ờm, bạn tự rút gọn nhé :) Mình đang hơi lười :b

\(y=sinx\Rightarrow y'=cosx;y''=-sinx;y'''=-cosx\)

Bằng quy nạp toán học ; ta c/m được : \(y^{\left(n\right)}sinx=sin\left(x+n\dfrac{\pi}{2}\right)\)

y’= 3x3-6x2-5+cosx. Do đó y”= 9x2-12x-sinx. Chọn đáp án B

a.

\(y'=\dfrac{\left(sinx+cosx\right)'}{2\sqrt{sinx+cosx}}=\dfrac{cosx-sinx}{2\sqrt{sinx+cosx}}\)

b.

\(y'=\dfrac{-4}{\left(x-1\right)^2}\)

Tiếp tuyến vuông góc với \(y=\dfrac{1}{4}x+5\) nên có hệ số góc thỏa mãn \(k.\left(\dfrac{1}{4}\right)=-1\Rightarrow k=-4\)

\(\Rightarrow\dfrac{-4}{\left(x-1\right)^2}=-4\Rightarrow\left(x-1\right)^2=1\)

\(\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=-3\\x=2\Rightarrow y=5\end{matrix}\right.\)

Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=-4x-3\\y=-4\left(x-2\right)+5\end{matrix}\right.\)

\(y'=\frac{\left(sinx-x.cosx\right)'\left(cosx-x.sinx\right)-\left(sinx-x.cosx\right).\left(cosx-x.sinx\right)'}{\left(cosx-x.sinx\right)^2}\)

\(=\frac{\left(cosx-cosx+x.sinx\right)\left(cosx-x.sinx\right)-\left(sinx-x.cosx\right)\left(-sinx-sinx-x.cosx\right)}{\left(cosx-x.sinx\right)^2}\)

\(=\frac{x.sinx.cosx-x^2sin^2x+sin^2x-x.cosx.sinx+sin^2x-x^2cos^2x}{\left(cosx-x.sinx\right)^2}\)

\(=\frac{2sin^2x-x^2\left(sin^2x+cos^2x\right)}{\left(cosx-x.sinx\right)^2}=\frac{2sin^2x-x^2}{\left(cosx-x.sinx\right)^2}\)