Tìm x để biểu thức sau có nghĩa :5/x
tìm x để biểu thức sau có nghĩa:
\(\dfrac{x-2\sqrt{x+5}}{\sqrt{2x^2+1}}\)
\(\dfrac{x-2\sqrt{x+5}}{\sqrt{2x^2+1}}\) có nghĩa khi
\(\left\{{}\begin{matrix}x+5\ge0\\2x^2+1>0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x\ge-5\\2x^2+1>0\forall x\in R\end{matrix}\right.\\ \Rightarrow x\ge-5\)
tìm x để biểu thức sau có nghĩa
a, \(\sqrt{2-4x}\)
b, \(\sqrt{4\left(x-5\right)}\)
\(a,ĐK:2-4x\ge0\Leftrightarrow x\le\dfrac{1}{2}\\ b,ĐK:4\left(x-5\right)\ge0\Leftrightarrow x-5\ge0\left(4>0\right)\Leftrightarrow x\ge5\)
Tìm điều kiện x để các biểu thức sau có nghĩa
\(\sqrt{x-5}\) \(\dfrac{1}{\sqrt{3x-2}}\)
`sqrt(x-5)` có nghĩa khi:
`x-5 ≥0`
`=> x ≥5`
Vậy `x≥5` thì `sqrt(x-5` có nghĩa
____________
`1/(sqrt(3x-2))` có nghĩa khi
`1/(sqrt(3x-2)) ≥0`
`⇒ 3x-2≥0`
` ⇒3x≥2`
` ⇒x≥2/3`
Vậy `x ≥2/3` thì `1/(sqrt(3x-2))` có nghĩa
Tìm x để các biểu thức sau có nghĩa và rút gọn các biểu thức sau: a) x-√x /√x-1 - x-1/√x+1
\(\dfrac{x-\sqrt{x}}{\sqrt{x}-1}-\dfrac{x-1}{\sqrt{x}+1}\);\(ĐK:x\ge0;x\ne1\)
\(\Leftrightarrow\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}-\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(\Leftrightarrow\sqrt{x}-\left(\sqrt{x}-1\right)\)
\(\Leftrightarrow\sqrt{x}-\sqrt{x}+1\)
\(\Leftrightarrow1\)
a: \(=\sqrt{x}\cdot\dfrac{\left(\sqrt{x}-1\right)}{\sqrt{x}-1}-\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(=\sqrt{x}-\sqrt{x}+1=1\)
Tìm x để biểu thức sau có nghĩa:
\(\sqrt{x-2}+\frac{1}{x-5}\)
Bài làm:
đkxđ: \(\hept{\begin{cases}x-5\ne0\\x-2\ge0\end{cases}\Rightarrow}\hept{\begin{cases}x\ne5\\x\ge2\end{cases}}\)
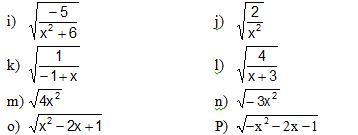 Tìm x để biểu thức sau có nghĩa
Tìm x để biểu thức sau có nghĩa
l, \(x+3>0\Leftrightarrow x>-3\)
m, \(4x^2\ge0\forall x\Rightarrow\) biểu thức xác định với mọi x.
n, \(-3x^2\ge0\Leftrightarrow x=0\)
o, \(x^2-2x+1=\left(x-1\right)^2\ge0\forall x\Rightarrow\) biểu thức xác định với mọi x.
p, \(-x^2-2x-1=-\left(x+1\right)^2\le0\)
Biểu thức xác định khi \(x+1=0\Leftrightarrow x=-1\)
i: ĐKXĐ: \(x\in\varnothing\)
j: ĐKXĐ: \(x\ne0\)
k: ĐKXĐ: x>1
1)
a) So sánh: - 2 và \(-\sqrt{5}\)
b) Tìm x để biểu thức sau có nghĩa: (Giải chi tiết từng bước)
\(\sqrt{\dfrac{10}{5-x}}\)
Lời giải:
$2=\sqrt{4}< \sqrt{5}$
$\Rightarrow -2> -\sqrt{5}$
b. Để biểu thức trên có nghĩa thì \(\left\{\begin{matrix} 5-x\neq 0\\ \frac{10}{5-x}\geq 0\end{matrix}\right.\Leftrightarrow 5-x>0\Leftrightarrow x<5\)
a: -2=-căn 4>-căn 5
b: ĐKXĐ: 10/5-x>=0
=>5-x>0
=>x<5
a) \(-2=-\sqrt{4}\\ \Rightarrow-\sqrt{4}>-\sqrt{5}\)
b) để biểu thức sau có nghĩa thì
\(\dfrac{10}{5-x}\ge0\\ mà.10>0\\ \Rightarrow5-x>0\\\Leftrightarrow x< 5 \)
Vạy x<5 thì biểu thức sau có nghĩa
tìm x để căn thúc sau có nghĩa
\(\sqrt{25-x^2}\)
M=\(\sqrt{x+4}+\sqrt{2-x}\) tìm x thuộc z đẻ biểu thức M có nghĩa
\(\sqrt{25-x^2}\) lớn hơn hoặc= 0
=> 25-x2 lớn hơn hoặc= 0
=> -x2 lớn hơn hoặc= -25
x2 bé hơn hoặc =25
x bé hơn hoặc =5
a: ĐKXĐ: \(-5\le x\le5\)
b: ĐKXĐ: \(-4\le x\le2\)
mà x nguyên
nên \(x\in\left\{-4;-3;-2;-1;0;1;2\right\}\)
Cho biểu thức
Q=\(\dfrac{\sqrt{x}}{\sqrt{x}-5}-\dfrac{10\sqrt{x}}{x-25}-\dfrac{5}{\sqrt{x}-5}\)
a) Tìm điều kiện của x để biểu thức có nghĩa. Rút gọn Q
b) tìm x để Q=\(\dfrac{-3}{7}\)
c)tìm x nguyên để phân thức Q nhân giá trị nguyên