Góc giữa hai đường thẳng y=2x và y=1/2.x+3 là ........ o

Những câu hỏi liên quan
Tìm số đo của góc giữa hai đường thẳng là đồ thị của hai hàm số \(y = x\) và \(y = 2x + 1\)
Từ đồ thị hàm số ta có phương trình tổng quát
\(y = x \Leftrightarrow {d_1}:x - y = 0\), \(y = 2x + 1 \Leftrightarrow 2x - y + 1 = 0\)
Từ đó ta có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {1; - 1} \right),\overrightarrow {{n_2}} = \left( {2; - 1} \right)\)
\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {1.2 + ( - 1).( - 1)} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} \sqrt {{2^2} + {{\left( { - 1} \right)}^2}} }} = \frac{{3\sqrt {10} }}{{10}} \Rightarrow \left( {{d_1},{d_2}} \right) \approx 18^\circ 26'\)
Vậy góc giữa hai đường thẳng có đồ thị đã cho gần bằng \(18^\circ 26'\)
Đúng 0
Bình luận (0)
Quan sát Hình 3.
a) So sánh hệ số góc của hai đường thẳng:
\(d:y = 2x + 3\) và \(d':y = 2x - 2\).
Nêu nhận xét về vị trí giữa hai đường thẳng này.
b) Tìm đường thẳng \(d''\) đi qua gốc tọa độ \(O\) và song song với đường thẳng \(d\).
a) Đường thẳng \(d:y = 2x + 3\) có hệ số góc là \(a = 2\).
Đường thẳng \(d':y = 2x - 2\) có hệ số góc là \(a' = 2\).
Hệ số góc của hai đường thẳng \(d\) và \(d'\) bằng nhau.
Từ đồ thị ta thấy, hai đường thẳng \(d\) và \(d'\) song song với nhau.
b) Đường thẳng \(d''\) đi qua gốc tọa độ \(O\) nên có dạng \(y = a''x\).
Từ đồ thị ta thấy, \(d''\) đi qua điểm \(\left( {1;2} \right)\) nên ta có:
\(2 = 1.a'' \Rightarrow a'' = 2\).
Do đó, đường thẳng \(d''\) là \(y = 2x\).
Đúng 1
Bình luận (0)
a. Vẽ đồ thị của 2 hàm số y=x-3 và y=-2x+3 trên cùng 1 mặt phẳng tọa độ
b. Hai đường thẳng y=x-3 và y=-2x+3 cắt nhau tại C . Tính tọa độ điểm C
c. Tính góc tạo bởi đường thẳng y=x-3 với trục Ox
d. Tìm m để đường thẳng y=(m+2)x+m và hai đường thẳng y=x-3 và y=-2x+3 đồng quy
b: Tọa độ điểm C là:
\(\left\{{}\begin{matrix}x-3=-2x+3\\y=x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho đường thẳng: left(dright):yleft(m-2right)x+m+3.a) Tìm m để (d) vuông góc với y2x-3 và đi qua điểm A(-2;-1). Từ đó tính khoảng cách giữa 2 đường thẳngb) Tìm m để (d) là tiếp tuyến của đường tròn left(O;sqrt{2}right) trong đó O là gốc tọa độc) Tìm m để (d) cắt đường thẳng y-2x+1 tại điểm B thuộc góc phần tư thứ nhất
Đọc tiếp
Cho đường thẳng: \(\left(d\right):y=\left(m-2\right)x+m+3\).
a) Tìm m để (d) vuông góc với y=2x-3 và đi qua điểm A(-2;-1). Từ đó tính khoảng cách giữa 2 đường thẳng
b) Tìm m để (d) là tiếp tuyến của đường tròn \(\left(O;\sqrt{2}\right)\) trong đó O là gốc tọa độ
c) Tìm m để (d) cắt đường thẳng y=-2x+1 tại điểm B thuộc góc phần tư thứ nhất
Cho hai đường thẳng d1: y 3x – 1 và
d
2
:
x
2
−
t
y
5
+
2
t
Góc giữa hai đường thẳng là: A.
α...
Đọc tiếp
Cho hai đường thẳng d1: y = 3x – 1 và d 2 : x = 2 − t y = 5 + 2 t Góc giữa hai đường thẳng là:
A. α = 30 °
B. α = 45 °
C. α = 60 °
D. α = 90 °
Hai đường thẳng lần lượt có các vectơ chỉ phương là u 1 = 1 ; 3 và u 2 = − 1 ; 2 nên ta có cos d 1 , d 2 = cos u 1 → , u 2 → = 1. − 1 + 3.2 1 2 + 3 2 . − 1 2 + 2 2 = 1 2 .
Do đó góc giữa hai đường thẳng là α = 45 ° . Đáp án là phương án B.
Đúng 0
Bình luận (0)
Đường thẳng vuông góc với hai đường thẳng
d
1
:
x
+
y
-
1
0
2
x
+
z
0
và
d
2...
Đọc tiếp
Đường thẳng vuông góc với hai đường thẳng d 1 : x + y - 1 = 0 2 x + z = 0 và d 2 : 2 x + y - 1 = 0 z - 2 = 0 là:
A. x - 3 y + 2 z + 3 = 0 2 x + y - 10 z + 19 = 0
B. 2 x - 3 y + z + 3 = 0 2 x + y - 10 z + 19 = 0
C. x - 3 y + 2 z + 3 = 0 3 x - y + 2 z + 14 = 0
D. x - y - 2 z + 9 = 0 2 x + y - 10 z + 5 = 0
Góc giữa hai đường thẳng d1: 3x + y - 3 = 0 và d2: 2x - y + 2 = 0 bằng bao nhiêu?
A. 30 °
B. 45 °
C. 60 °
D. 90 °
Đáp án: B
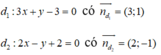
Gọi góc giữa hai đường thẳng là α
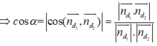
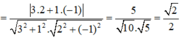
⇒ α = 45 °
Đúng 0
Bình luận (0)
vẽ đồ thị của hai hàm số y = 2x + 1 và y = -x + 1 trên cùng mặt phẳng
Tính số đo góc a tại bởi đường thẳng y = 2x + 1 và trục Ox?
Gọi Giao điểm của đường thẳng y = 2x + 1 và đường thẳng y = -x + 1 là A. Giao điểm của đường thẳng y = 2x + 1 và trục Ox là B, Giao điểm của đường thẳng y = -x + 1 và trục Ox là C. Tính diện tích tam giác ABC
Tính số đo góc giữa hai đường thẳng \({d_1}:2x--y + 5 = 0\) và\({d_2}:x - 3y + 3 = 0\).
Vecto pháp tuyến của đường thẳng \({d_1}\) là: \(\overrightarrow {{n_1}} = \left( {2; - 1} \right)\)
Vecto pháp tuyến của đường thẳng \({d_2}\) là: \(\overrightarrow {{n_2}} = \left( {1; - 3} \right)\)
Ta có: \(\cos \left( {{d_1},{d_2}} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {2.1 + \left( { - 1} \right).\left( { - 3} \right)} \right|}}{{\sqrt {{{\left( 2 \right)}^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{1^2} + {{\left( { - 3} \right)}^2}} }} = \frac{{\sqrt 2 }}{2}\)
Vậy \(\left( {{d_1},{d_2}} \right) = {45^o}\)
Đúng 0
Bình luận (0)












