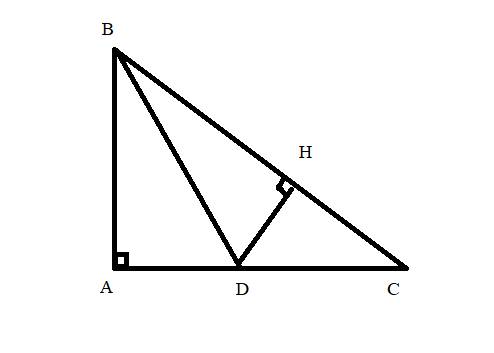
cho tam giác abc vuông tại b,phaan GIÁC AD từ d kẻ dh vuông góc với ac (h thuộc ac); hd và ab koes dài cắt nhau tại i chưng minh bh song song với ic

Những câu hỏi liên quan
Cho tam giác ABC vuông tại B,p/g AD.Từ D,kẻ DH vuông góc AC(H thuộc AC).HD và AB kéo dài cắt nhau tại I.CMR:
a)Tam giác ABD=tam giác AHD
b)AD là trung trực
c)DIC cân
d)BH//IC
e)AD vuông góc với IC
f)BD<DC
Cho tam giác abc vuông tại a có ab=12cm, bc= 13cm a. Tính ac b. Tia phân giác của góc b cắt ac ở d. Tính ad, cd c. Kẻ dh vuông góc với bc(h thuộc bc). Tính dh d. Kẻ hi vuông góc với ab( i thuộc ab). Tính diện tích tứ giá
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=BC^2-AB^2=13^2-12^2=169-144=25\)
=>\(AC=\sqrt{25}=5\left(cm\right)\)
b: XétΔBAC có BD là phân giác
nên \(\dfrac{AD}{BA}=\dfrac{CD}{BC}\)
=>\(\dfrac{AD}{12}=\dfrac{CD}{13}\)
D nằm giữa A và C
=>AD+DC=AC
=>AD+DC=5(cm)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{12}=\dfrac{CD}{13}=\dfrac{AD+CD}{12+13}=\dfrac{5}{25}=0,2\)
=>\(AD=2\cdot12=2,4\left(cm\right);CD=2\cdot13=2,6\left(cm\right)\)
c: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔBAD=ΔBHD
=>DA=DH
mà DA=2,4(cm)
nên DH=2,4(cm)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A. Đường phân giác BD ( D thuộc AC). Kẻ DH vuông góc với BC ( H thuộc BC ). a,CMR:tam giác ABD và tam giác HBD b,so sánh AD & DC
a, Ta có: \(BD\) là phân giác \(\widehat{ABC}\)
\(\Rightarrow\widehat{ABD}=\widehat{HBD}\left(tc\right)\)
\(\)Xét ΔABD vuông tại A và ΔHBD vuông tại H có:
\(BDchung\)
\(\widehat{ABD}=\widehat{HBD}\left(cmt\right)\)
\(\Rightarrow\) ΔABD = ΔHBD ( ch.gn )
b, Ta có: ΔABD = ΔHBD ( cmt )
\(\Rightarrow AD=DH\left(2ctu\right)\)
Xét ΔDHC vuông tại H có:
HC là cạnh huyền
\(\Rightarrow\) HC là cạnh lớn nhất
⇒ \(DH< CH\)
Mà \(DH=AD\)
\(\Rightarrow AD< CH\)
Đúng 1
Bình luận (1)
a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
b: ΔBAD=ΔBHD
=>DA=DH
mà DH<DC
nên DA<DC
Đúng 0
Bình luận (1)
Cho tam giác ABC vuông tại A. Đường phân giác BD ( D thuộc AC). Kẻ DH vuông góc với BC ( H thuộc BC ). a,CMR:tam giác ABD và tam giác HBD b,so sánh AD & DC
Cho tam giác ABC vuông tại A . Tia phân giác của góc B cắt AC tại D . Kẻ DH vuông góc với BC ( H thuộc BC ) và DH cắt AB tại K . CM :
a. AD = DH
b. AD < DC
c. TAm giác KBC cân
a)xét 2 tam giác vuông ABD và HBD có:
BD(chung)
ABD=CBD(gt)
suy ra tam giác ABD=HBD(CH-GN)
suy ra AD=DH
b)
ta có: tam giác HCD vuông tại H sủy a DC là cạnh lớn nhất trong tam giác đó
suy ra DC>DH mà DH=Ad suy ra AD<DC
Đúng 0
Bình luận (0)
c)
xét 2 tam giác vuông BHK và BAC có:
BA=BH(cmt)
BHK=BAC=90
B(chung)
suy ra : tam giác BHK=BAC(g.c.g)
suy ra BC=BK
suy ra tma giác BKC cân tại B
Đúng 0
Bình luận (0)
a, Xét tg ABD và BDH :
Ta có : A=H=90 ( vuông nhau )
BD cạnh chung
góc ADB = góc DBH
=> tg ABD = tg DBH ( gcg)
=>AD=DH (2 cạnh tương ứng)
b, Xét tg DHC vuông tại H
Mà H là góc lớn nhất
=> DC là cạnh lớn nhất
Mà : trong tg DHC có :
DC > DH
Nên : DC> DH=AD
Vậy : DC>AD
c, k pt
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại C. Có góc A = 60 độ. AD là tia phân giác của CAB(D thuộc BC). Qua B kẻ đường thẳng vuông góc với tia AD tại E cắt đường thẳng AC tại I, kẻ DH vuông góc với AB tại H
a/ Chứng minh AH = HB, AH=AC
b/chứng minh tam giác ACB bằng tam giác BEA
c/ chứng minh AC,BE,DH đồng quy
d/ tam giác AIB là tam giác gì?
Cho tam giác ABC vuông tại A, kẻ đường phân giác BD từ D, kẻ DH vuông góc với BC(H thuộc BC)
a) CM: AD=Dh
b) So sánh AD và DC
c) Có AB=6cm,AC=8cm. Tính HD
Mình nói tóm tắt thôi nhé!
a) chứng minh được tam giác ABD = tam giác HBD (cạnh huyền - góc nhọn) => AD = DH (2 cạnh tương ứng)
b) tam giác HDC vuông tại H nên DC là cạnh lớn nhất => DC > DH; mà DH = AH (c/m trên) => DC > AD
c) Mình chưa nghĩ ra![]()
Đúng 0
Bình luận (0)
Câu c là tính HC nhé bạn!
c) Tính BC bằng cách dùng định lí pytago trong tam giác ABC, ta có: BC = 10cm
BH + HC = BC = 10cm
BH = AB = 6cm
=> HC = 10 - 6 = 4 cm
Chúc bạn học tốt!![]()
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A.Kẻ BD là tia phân giác của góc ABC ( D thuộc AC).Từ D,kẻ DH vuông góc với BC(H thuộc BC).Tia BA cắt HD tại K.Kéo dài BD cắt KC tại E.
/chứng minh 2(AD + AH) > KC/
Cho tam giác ABC vuông tại A. Tia phân giác của góc ABC cắt AC tại D. Từ D kẻ DH vuông góc với BC tại H và DH cắt AB tại K.a. Chứng minh: AD HD b. So sánh độ dài cạnh AD và DC c. Chứng minh tam giác KBC là tam giác cân.
Đọc tiếp
Cho tam giác ABC vuông tại A. Tia phân giác của góc ABC cắt AC tại D. Từ D kẻ DH vuông góc với BC tại H và DH cắt AB tại K.
a. Chứng minh: AD = HD
b. So sánh độ dài cạnh AD và DC c. Chứng minh tam giác KBC là tam giác cân.
a: Xét ΔBAD vuông tai A và ΔBHD vuông tại H có
BD chung
góc ABD=góc HBD
Do đó: ΔBAD=ΔBHD
Suy ra: AD=HD
b: ta có: AD=HD
mà HD<DC
nen AD<DC
c: Xét ΔBHK vuông tại H và ΔBAC vuông tạiA có
BH=BA
góc HBK chung
Do đó:ΔBHK=ΔBAC
Suy ra BK=BC
hay ΔBKC cân tại B
Đúng 0
Bình luận (0)