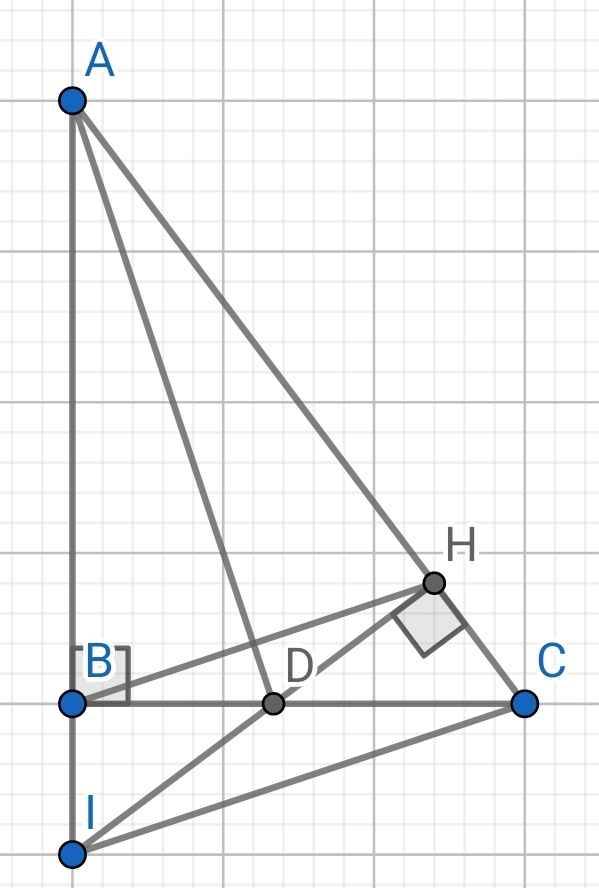
Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠CAD
⇒ ∠BAD = ∠HAD
Xét hai tam giác vuông: ∆BAD và ∆HAD có:
AD là cạnh chung
∠BAD = ∠HAD (cmt)
⇒ ∆BAD = ∆HAD (cạnh huyền - góc nhọn)
⇒ BD = HD (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆IBD và ∆CHD có:
BD = HD (cmt)
∠BDI = ∠HDI (đối đỉnh)
⇒ ∆IBD = ∆CHD (cạnh góc vuông - góc nhọn kề)
⇒ BI = HC (hai cạnh tương ứng)
Do ∆BAD = ∆HAD (cmt)
⇒ AB = AH (hai cạnh tương ứng)
⇒ ∆ABH cân tại A
⇒ ∠ABH = ∠AHB = (180⁰ - ∠BAH) : 2 (1)
Ta có:
AI = AB + BI
AC = AH + HC
Mà AB = AH (cmt)
BI = HC (cmt)
⇒ AI = AC
⇒ ∆AIC cân tại A
⇒ ∠AIC = ∠ACI = (180⁰ - ∠IAC) : 2
= (180⁰ - ∠BAH) : 2 (2)
Từ (1) và (2) ⇒ ∠ABH = ∠AIC
Mà ∠ABH và ∠AIC là hai góc đồng vị
⇒ BH // CI












