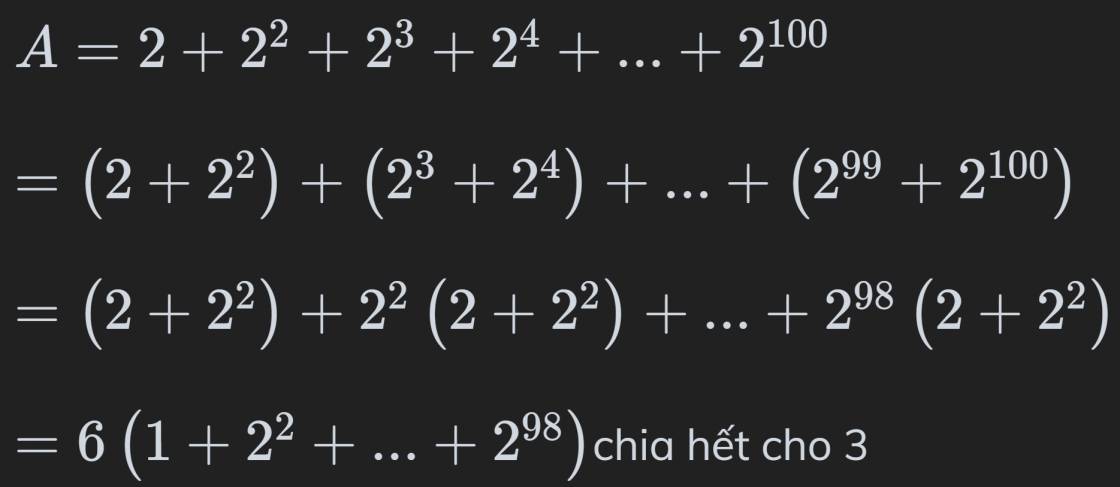A = 2 + 22+ 23+ ... + 2100chia hết cho 3 và 6

Những câu hỏi liên quan
chứng tỏ Rằng A= 2+22+23+...+2100chia hết cho 6
\(A=2+2^2+2^3+...+2^{100}\)
\(\Rightarrow A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{99}+2^{100}\right)\)
\(\Rightarrow A=6+2^3\left(2+2^2\right)+...+2^{99}\left(2+2^2\right)\)
\(\Rightarrow A=6+2^3.6+...+2^{99}.6\)
\(\Rightarrow A=6\left(1+2^3+...+2^{99}\right)⋮6\)
Đúng 2
Bình luận (0)
Chứng tỏ rằng : A=2 + 22+23+24+....+299+ 2100chia hết cho 3
Mong giúp đỡ mai thi rùi =(
Ta có: A=2+22+23+24+...+299+2100
-> A=2(1+2)+23(1+2)+...+299(1+2)
->A=2.3+23.3+...+299.3
->A=3(2+23+...+299)\(⋮\)3
=> Đpcm
Đúng 2
Bình luận (0)
Chứng minh rằng: 1+22+24+26+.....+2100chia hết cho 21.
Lời giải:
$A=1+2^2+2^4+...+2^{100}$
$=(1+2^2+2^4)+(2^6+2^8+2^{10})+....+(2^{96}+2^{98}+2^{100})$
$=(1+2^2+2^4)+2^6(1+2^2+2^4)+....+2^{96}(1+2^2+2^4)$
$=(1+2^2+2^4)(1+2^6+...+2^{96})$
$=21(1+2^6+...+2^{96})\vdots 21$
Đúng 1
Bình luận (0)
Câu 6: Chứng tỏ A = 2 + 22 + 23 + 24….+ 259 + 260
a. Chia hết cho 3;
b. Chia hết cho 7.
A= (2+22)+(23+24)+...+(259+260)
A=2.(1+2)+23.(1+2)+...+259.(1+2)
A=2.3+23.3+...+259.3
A=3.(2+23+...+259)
Vì 3 chia hết cho 3 => 3.(2+23+...+259) chia hết cho 3
=>A chia hết cho 3
A= (2+22+23)+...+(258+259+260)
A=2.(1+2+22)+...+258.(1+2+22)
A=2.7+...+258.7
A=7.(2+...+258)
Vì 7 chia hết cho 7 =>7.(2+...+258) chia hết cho 7
CHIA HẾT CHO 3 :
A= (2+22)+(23+24)+...+(259+260)
A=2.(1+2)+23.(1+2)+...+259.(1+2)
A=2.3+23.3+...+259.3
A=3.(2+23+...+259)
Vì 3 chia hết cho 3 => 3.(2+23+...+259) chia hết cho 3
=>A chia hết cho 3
Cho A 2 22 23 24 ....... 2100 .Chứng mih rằng A chia hết cho 3, cho 6
\(A=2+2^2+2^3+2^4+...+2^{100}\)
\(=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{99}+2^{100}\right)\)
\(=\left(2+2^2\right)+2^2\left(2+2^2\right)+...+2^{98}\left(2+2^2\right)\)
\(=6\left(1+2^2+...+2^{98}\right)\)chia hết cho \(6\).
Cho a thuộcZ CM : a^3- 19a chia hết cho 6
Cho A = 1 + 3 + 3^2 + ...+ 3^21 + 3^22 + 3^ 23 .CM
a) A chia hết cho 13
b) A chía hết cho 40
Chứng minh: A = 21 22 23 24 ... 22010 chia hết cho 3 và 7 Chứng minh: A = 21 22 23 24 ... 22010 chia hết cho 3 và 7
Ta có :
\(A=2+2^2+2^3+2^4...2^{2010}\)\(^0\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{2009}\left(1+2\right)\)
\(=2.3+2^3.3+....+2^{2009}.3\)
\(=3\left(2+2^3+....+2^{2009}\right)⋮3\)
Ta có :
\(2+2^2+2^3+2^4+....+2^{2010}\)
\(=2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{2008}\left(1+2+2^2\right)\)
\(=2.7+2^4.7+....+2^{2008}.7\)
\(=7\left(2+2^4+....+2^{2008}\right)⋮7\)
Vậy \(2^1+2^2+2^3+2^4+...+2^{2010}⋮3\) và \(7\)
a. Chứng minh A=21+22+23+24+...+2100 chia hết cho 3
b. Chứng minh B=31+32+33+34+...+299chia hết cho 13
c. Chứng minh C=51+52+53+54+...+5105 chia hết cho 6 và 31
Chứng tỏ rằng A = 2 + 22 + 23 + …+ 2100 chia hết cho 6.
\(A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{99}+2^{100}\right)\\ A=\left(2+2^2\right)+2^2\left(2+2^2\right)+...+2^{98}\left(2+2^2\right)\\ A=\left(2+2^2\right)\left(1+2^2+...+2^{98}\right)\\ A=6\left(1+2^2+...+2^{98}\right)⋮6\)
Đúng 2
Bình luận (0)