Câu 24: Trong mặt phẳng Oxy, cho hai điểm A(1;2) và B(-1;3). Tìm toạ độ điểm M trên trục Oy sao cho tam giác ABM vuông tại B
A. M(0;-2)
B. M(0;4)
C. M(0;5)
D. M(0;-4)
câu 173. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A(2,3) và B(1,4) . Đường thẳng nào cách đều hai điểm A và B?
Lời giải:
Đường trung trực của $AB$ sẽ cách đều 2 điểm $A,B$. Gọi đường này là $d$
$\overrightarrow{n_d}=\overrightarrow{AB}=(-1,1)$
$(d)$ là đường trung trực của $AB$ nên đi qua trung điểm $I(\frac{3}{2}, \frac{7}{2})$ của $AB$
Do đó PTĐT $(d)$ là:
$-1(x-\frac{3}{2})+1(y-\frac{7}{2}=0$
$\Leftrightarrow -x+y-2=0$
Câu hỏi: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;3) và B(-1;2). Tìm N để A,B,N thẳng hàng.
Có vô số điểm N để A,B,N thẳng hàng, cho nên để tìm ra 1 điểm N cụ thể thì cần thêm điều kiện nữa (ví dụ N thuộc Ox, Oy hoặc đường thẳng nào đó)
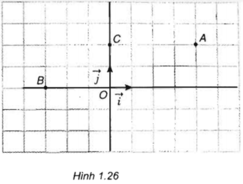
Câu hỏi 3 trang 24: Tìm tọa độ của các điểm A, B, C trong hình 1.26. Cho ba điểm D(-2; 3), E(0; -4), F(3; 0). Hãy vẽ các điểm D, E, F trên mặt phẳng Oxy.
Câu 3: Trong mặt phẳng Oxy, cho hai điểm A(1;-2), B(3;1). Viết phương trình tham số của đường thẳng d đi qua hai điểm A và B.
Câu 4: Cho hai điểm A(4; -3), B(2;1). Viết phương trình đường tròn (C) nhận AB làm đường kính
Câu 4:
Tọa độtâm I là;
x=(4+2)/2=3 và y=(-3+1)/2=-1
I(3;-1); A(4;-3)
IA=căn (4-3)^2+(-3+1)^2=căn 5
=>(C): (x-3)^2+(y+1)^2=5
Câu 3:
vecto AB=(2;3)
PTTS là:
x=1+2t và y=-2+3t
Giúp em bài này với ạ:
Câu 16: Trong mặt phẳng toạ độ Oxy, cho hai điểm A(1;-2) ; B(3;2). Tìm điểm M sao cho B là trung điểm của đoạn thẳng AM
A. M(5;6)
B. M(2;0)
C. M(4;0)
D. M(-1;-6)
Theo công thức trung điểm:
\(\left\{{}\begin{matrix}x_M=2x_B-x_A=5\\y_M=2y_B-y_A=6\end{matrix}\right.\) \(\Rightarrow M\left(5;6\right)\)
Để B là trung điểm của đoạn thẳng AM, ta cần tìm tọa độ của điểm M.
Theo định nghĩa, trung điểm của một đoạn thẳng là điểm nằm ở giữa hai đầu mút của đoạn đó. Ta áp dụng công thức trung điểm để tìm tọa độ của M.
Công thức trung điểm: M(xM, yM) là trung điểm của đoạn AB <=> (xM, yM) = ((xA + xB)/2, (yA + yB)/2).
Ứng với A(1; -2) và B(3; 2): xM = (1 + 3)/2 = 2, yM = (-2 + 2)/2 = 0.
Vậy tọa độ của điểm M là M(2; 0).
Đáp án đúng là: B. M(2; 0).
1. Trong mặt phẳng Oxy, cho đường tròn (C): \(x^2+y^2-2x+4y-4=0\)và điểm M(-1;-3). Gọi I là tâm của (C). Viết phương trình đường thẳng đi qua M và cắt (C) tại hai điểm A,B sao cho tam giác IAB có diện tích lớn nhất
2. Trong mặt phẳng Oxy, cho đường tròn (C): \(x^2+y^2+4x+4y-17=0\) và điểm A(6;17). Viết phương trình tiếp tuyến của (C) biế tiếp tuyến đi qua điểm A.
Trong mặt phẳng tọa độ Oxy , cho hai điểm A(-1,1), B (1,-1) .Tìm tọa độ điểm C sao cho tam giác ABC vuông cân tại A
Trong mặt phẳng Oxy, cho hai điểm A(1;-2), B(3;1). Viết phương trình tham số của đường thẳng d đi qua hai điểm A và B.
vecto AB=(2;3)
PTTS AB là;
x=1+2t và y=-2+3t
trong mặt phẳng Oxy cho hai điểm A(-1;5) và B(3;-1) trung điểm I của đoạn thẳng AB có độ là
\(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=\dfrac{-1+3}{2}=1\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{5+\left(-1\right)}{2}=2\end{matrix}\right.\)
\(\Rightarrow I\left(1;2\right)\)