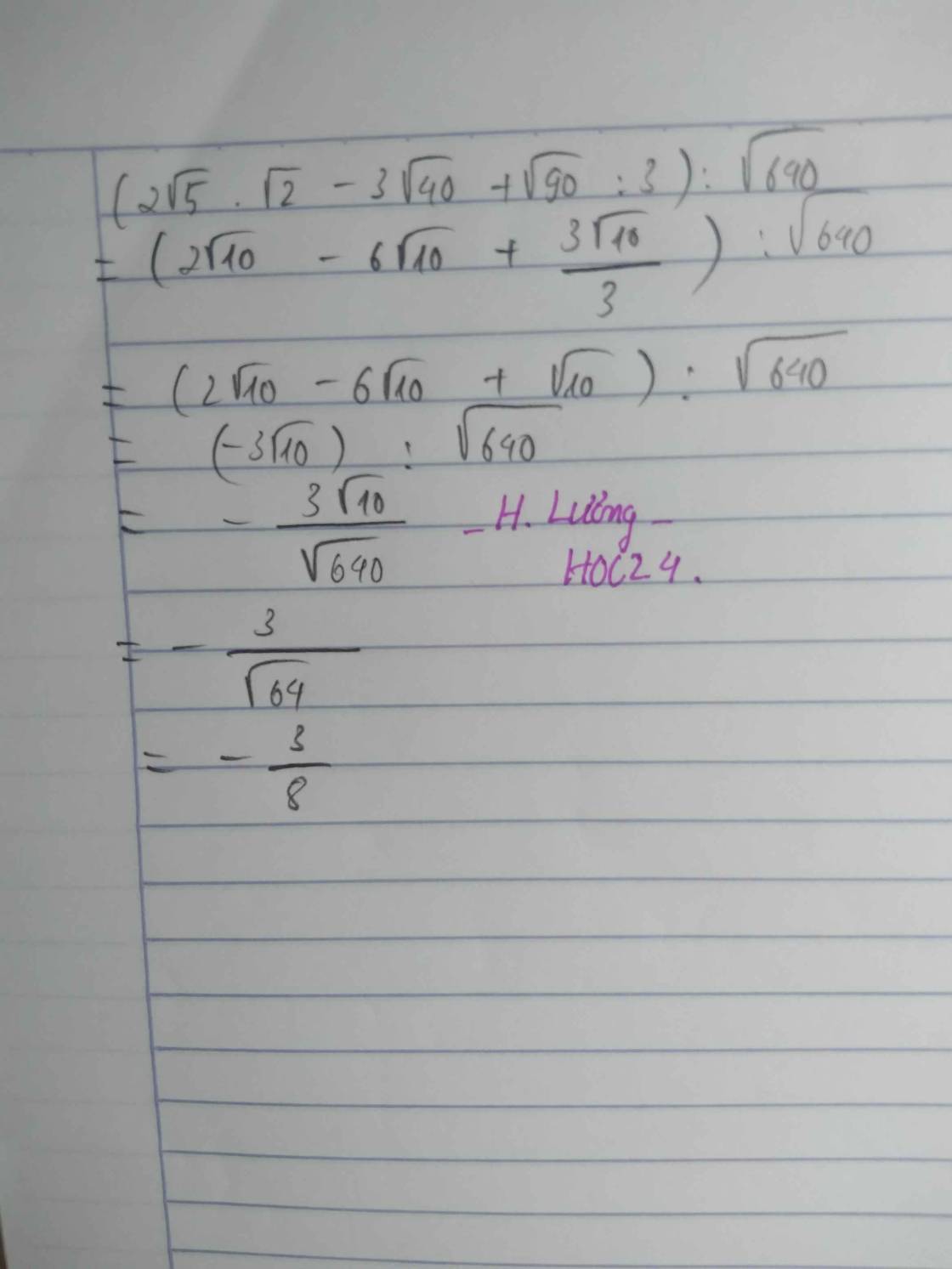\(\sqrt{\left(\sqrt{3}-\sqrt{5}\right)^2}-\sqrt{\left(1-\sqrt{5}\right)^2}+\dfrac{3}{\sqrt{3}}\)

\(=\left|\sqrt{3}-\sqrt{5}\right|-\left|1-\sqrt{5}\right|+\dfrac{\left(\sqrt{3}\right)^2}{\sqrt{3}}\)

\(=\left(\sqrt{5}-\sqrt{3}\right)-\left(\sqrt{5}-1\right)+\sqrt{3}\)

\(=\sqrt{5}-\sqrt{3}-\sqrt{5}+1+\sqrt{3}\)

\(=1\)

\(\sqrt{4-2\sqrt3}-\sqrt{4+2\sqrt3}\)

\(=\sqrt{\left(\sqrt3-1\right)^2}-\sqrt{\left(\sqrt3+1\right)^2}\)

\(=\left|\sqrt3-1\right|-\left|\sqrt3+1\right|\)

\(=\left(\sqrt3-1\right)-\left(\sqrt3+1\right)\)

\(=\sqrt3-1-\sqrt3-1\)

\(=-2\)

Ta cần tính giá trị của biểu thức sau:

\(\frac{6 + 2}{5} - \frac{6 - 2}{5}\)

\(\frac{8}{5} - \frac{4}{5} = \frac{8 - 4}{5} = \frac{4}{5}\)

\(\boxed{\frac{4}{5}}\)

✅ Giá trị của biểu thức là \(\frac{4}{5}\).

a)   \(A=\sqrt{2-\sqrt{3}}+\sqrt{2+\sqrt{3}}\)

\(\Rightarrow\)\(\sqrt{2}A=\sqrt{4-2\sqrt{3}}+\sqrt{4+2\sqrt{3}}\)

                       \(=\sqrt{\left(\sqrt{3}-1\right)^2}+\sqrt{\left(\sqrt{3}+1\right)^2}\)

                        \(=\sqrt{3}-1+\sqrt{3}+1=2\sqrt{3}\)

\(\Rightarrow\)\(A=\frac{2\sqrt{3}}{\sqrt{2}}=\sqrt{6}\)

b) bn lm tương tự 

1: \(=\dfrac{\sqrt{4-2\sqrt{3}}+\sqrt{4+2\sqrt{3}}}{\sqrt{2}}\)

\(=\dfrac{\sqrt{3}-1+\sqrt{3}+1}{\sqrt{2}}=\dfrac{2\sqrt{3}}{\sqrt{2}}=\sqrt{6}\)

2: \(=\dfrac{\sqrt{6-2\sqrt{5}}-\sqrt{6+2\sqrt{5}}}{\sqrt{2}}\)

\(=\dfrac{\sqrt{5}-1-\sqrt{5}-1}{\sqrt{2}}=-\sqrt{2}\)

\(\left(3\sqrt{12}-4\sqrt{3}+\sqrt{15}\right)\cdot\sqrt{3}-2\sqrt{5}\)

\(=\left(6\sqrt{3}-4\sqrt{3}+\sqrt{15}\right)\cdot\sqrt{3}-2\sqrt{5}\)

\(=6+3\sqrt{5}-2\sqrt{5}=6+\sqrt{5}\)

(3\(\sqrt{12}\)-4\(\sqrt{3}\)+\(\sqrt{15}\)).\(\sqrt{3}\)-2\(\sqrt{5}\)

=\(\left(6\sqrt{3}-4\sqrt{3}+\sqrt{15}\right).\sqrt{3}-2\sqrt{5}\)

=\(\left(2\sqrt{3}+\sqrt{15}\right).\sqrt{3}-2\sqrt{5}\)

=\(6+\sqrt{45}-2\sqrt{5}\)

=\(6+3\sqrt{5}-2\sqrt{5}\)

=\(6+\sqrt{5}\)

a, \(\sqrt{\left(\sqrt{5}-4\right)^2}-\sqrt{5}+\sqrt{20}=4\)

\(VT=\sqrt{\left(4-\sqrt{5}\right)^2}-\sqrt{5}+\sqrt{20}=\left|4-\sqrt{5}\right|-\sqrt{5}+\sqrt{20}\)

\(=4-\sqrt{5}-\sqrt{5}+2\sqrt{5}=4\) hay \(VT=VP\)

Vậy ta có đpcm 

b, Với \(x>0,x\ne4\)

\(P=\left(\frac{1}{\sqrt{x}+2}+\frac{1}{\sqrt{x}-2}\right):\frac{2}{x-2\sqrt{x}}\)

\(=\left(\frac{\sqrt{x}-2+\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\right):\frac{2}{\sqrt{x}\left(\sqrt{x}-2\right)}\)

\(=\frac{2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}.\frac{\sqrt{x}\left(\sqrt{x}-2\right)}{2}=\frac{x}{\sqrt{x}+2}\)

1.

Giả sử điều trên là đúng ta có:

\( \left | \sqrt{5}-4 \right |-\sqrt{5}+\sqrt{20}=4\)

Ta có: \(4>\sqrt{5}\)

\(\Rightarrow 4-\sqrt{5}- \sqrt{5}+\sqrt{20}=4\)

\(\Leftrightarrow 4-\sqrt{20}+\sqrt{20}=4\)

\(\Rightarrow đpcm\)

2.

 \(P=\dfrac{x}{\sqrt{x}+2}\)

  Chúc Bạn Học Tốt.

\(\left| { - 3,14} \right| = 3,14;{\rm{ }}\,\,\,\left| {41} \right| = 41;{\rm{ }}\left| { - 5} \right| = 5;{\rm{ }}\left| {1,\left( 2 \right)} \right| = 1,(2);{\rm{ }}\left| {-  \sqrt 5} \right| =  \sqrt 5.\)

?

Để biểu diễn các số **2**, **3**, **4**, **5** trên **trục số**, bạn thực hiện như sau:

---

### ✅ **Các bước biểu diễn trên trục số:**

1. **Vẽ một trục số ngang** (đường thẳng có mũi tên 2 đầu).

2. **Chọn một điểm làm gốc** (thường là số 0).

3. Đánh dấu các điểm cách đều nhau và đánh số: 1, 2, 3, 4, 5,...

4. Xác định và **gạch đậm** hoặc **đánh dấu rõ** tại các điểm **2**, **3**, **4**, và **5**.

5. (Nếu yêu cầu cụ thể hơn: dùng chấm tròn tô màu, hoặc ký hiệu rõ từng số.)

---

### 📌 **Minh họa sơ bộ bằng ký hiệu ASCII (đơn giản):**

```

------|------|------|------|------|------|------>

1 2 3 4 5 6

● ● ● ●

(2) (3) (4) (5)

```

---

### 📌 Gợi ý vẽ bằng tay hoặc phần mềm:

* Nếu vẽ trên giấy: dùng thước và chia đều các đoạn.

* Nếu dùng phần mềm: bạn có thể vẽ bằng **GeoGebra**, **Paint**, hoặc chèn trong Word bằng công cụ **Shapes → Line + Text Box**.

---

Nếu bạn muốn, mình có thể **vẽ trục số với các điểm đó** bằng hình ảnh cho bạn. Bạn muốn mình gửi hình ảnh không?