(d):y=(2m+1)x-2 (m tham số)
Tìm m để (d) cắt các trục độ tạo thành tam giác có diện tích bằng 1
Cho hàm số bậc nhất y = (2m + 1)x - 2 (với m là tham số, m khác -1/2 )
Tìm m để đường thẳng (d) cắt các trục tọa độ tạo thành tam giác có diện tích bằng 1(đơn vị diện tích).
Cho hàm số y=(2m+1)x-2 (m#-1/2) Tìm m để (d) cắt các trục tọa độ tạo thành tam giác có diện tích =1 (đơn vị diện tích)
cho đường thẳng d: y = (2m+1)x -1 tìm m để d cắt 2 trục toạ độ tạo thành tam giác có diện tích =1/2
Gọi A,B lần lượt là giao của (d) với trục Ox và Oy
Tọa độ A là:
y=0 và (2m+1)x-1=0
=>x=1/(2m+1) và y=0
=>OA=1/|2m+1|
Tọa độ B là:
x=0 và y=-1
=>OB=1
Theo đề, ta có: S OAB=1/2
=>1/2*OA*OB=1/2
=>1/|2m+1|=1
=>|2m+1|=1
=>2m+1=1 hoặc 2m+1=-1
=>m=-1 hoặc m=0
cho đường thẳng (d) có phương trình:
\(\left(m+1\right)x+\left(m-2\right)y=3\) (d) ( m là tham số)
Tìm m để (d) cắt 2 trục tọa độ và tạo thành tam giác có diện tích bằng \(\dfrac{9}{2}\)
\(\left(m+1\right)x+\left(m-2\right)y=3\)\(\left(m\ne-1;m\ne2\right)\)
\(y=0\Leftrightarrow x=\dfrac{3}{m+1}\Rightarrow A\left(\dfrac{3}{m+1};0\right)\Rightarrow OA=\left|\dfrac{3}{m+1}\right|\)
\(x=0\Leftrightarrow y=\dfrac{3}{m-2}\Leftrightarrow B\left(0;\dfrac{3}{m-2}\right)\Rightarrow OB=\left|\dfrac{3}{m-2}\right|\)
\(S_{_{ }^{ }\Delta ABO}=\dfrac{9}{2}=\dfrac{1}{2}OA.OB=\dfrac{1}{2}.\dfrac{9}{\left|m+1\right|.\left|m-2\right|}\Leftrightarrow\dfrac{1}{\left|m+1\right|.\left|m-2\right|}=9\Leftrightarrow\left|m+1\right|.\left|m-2\right|=9\Leftrightarrow\left(m+1\right)^2.\left(m-2\right)^2-81=0\Leftrightarrow\left(m^2-m-11\right)\left(m^2-m+7\right)=0\Leftrightarrow\left[{}\begin{matrix}m^2-m-11=0\Leftrightarrow m=\dfrac{1\pm3\sqrt{5}}{2}\left(tm\right)\\m^2-m+7=0\left(vô-nghiệm\right)\end{matrix}\right.\)
\(\Rightarrow m=\dfrac{1\pm3\sqrt{5}}{2}\)
Cho x = 0 => \(y=\dfrac{3}{m-2}\)
vậy d cắt Oy tại A(0;3/m-2) => Oy = \(\left|\dfrac{3}{m-2}\right|\)
Cho y = 0 => \(x=\dfrac{3}{m+1}\)
vậy d cắt Ox tại B(3/m+1;0) => Ox = \(\left|\dfrac{3}{m+1}\right|\)
Ta có : \(S_{OAB}=\dfrac{1}{2}.OB.OA=\dfrac{1}{2}.\dfrac{9}{\left|\left(m+1\right)\left(m-2\right)\right|}=\dfrac{9}{2}\)
\(\Leftrightarrow\left|\left(m+1\right)\left(m-2\right)\right|=1\Leftrightarrow\left[{}\begin{matrix}m^2-m-3=0\\m^2-m-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{1+\sqrt{13}}{2};m=\dfrac{1-\sqrt{13}}{2}\\m=\dfrac{1+\sqrt{5}}{2};m=\dfrac{1-\sqrt{5}}{2}\end{matrix}\right.\)
Cho đường thẳng (d) có phương trình:
(m+1)x+(m-2)y=3 (d) (m là tham số)
a) Tìm giá trị của m biết đường thẳng (d) đi qua điểm A(-1;-2)
b) Tìm m để (d) cắt 2 trục tọa độ và tạo thành tam giác có diện tích bằng 9/2
Cho đường thẳng d : y = 2 m + 1 x − 1 . Tìm m để đường thẳng d cắt hai trục tọa độ tạo thành tam giác có diện tích bằng 1 2
A. m = 0
B. m = 1
C. m = − 1
D. Cả A và C đều đúng
d ∩ O y = B ⇒ x B = 0 ⇒ y B = − 1 ⇒ B 0 ; − 1 ⇒ O B = − 1 = 1 d ∩ O x = A ⇒ y A = 0 2 m + 1 x – 1 = 0 ⇔ x A = 1 2 m + 1 m ≠ − 1 2
⇒ A 1 2 m + 1 ; 0 ⇒ O A = 1 2 m + 1
S Δ A O B = 1 2 O A . O B = 1 2 .1. 1 2 m + 1 = 1 2 ⇔ | 2 m + 1 | = 1 ⇔ m = 0 m = − 1
Đáp án cần chọn là: D
ĐK: \(m\ne-2\)
\(x=0\Rightarrow y=2m+4\)
\(y=0\Rightarrow x=-2\)
\(S=\dfrac{1}{2}.2.\left|2m+4\right|=9\Leftrightarrow\left[{}\begin{matrix}m=-\dfrac{13}{2}\\m=\dfrac{5}{2}\end{matrix}\right.\)
Cho hàm số y =(m – 3)x + 2 có đồ thị là (d)
c) Tìm m để (d) cắt hai trục tọa độ tạo thành một tam giác có diện tích bằng 4.
c) y = (m – 3)x + 2 (m ≠ 3)
Gọi A, B lần lượt là giao điểm của (d) và trục Ox, Oy và tam giác tạo thành là tam giác AOB vuông tại O
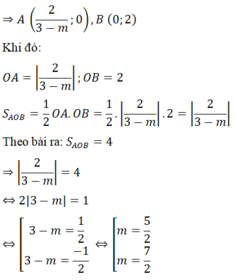
Cho đường thẳng d: y = ( k – 2 ) x – 1 . Tìm k để d cắt 2 trục tọa độ tạo thành tam giác có diện tích bằng 1
A. k = 5 2
B. k = 3 2
C. k = 1
D. Cả A và B đều đúng
d ∩ O y = B ⇒ x B = 0 ⇒ y B = − 1 ⇒ B 0 ; − 1 ⇒ O B = − 1 = 1 d ∩ O x = A ⇒ y A = 0 ⇔ k – 2 x A − 1 = 0 ⇔ x A = 1 k − 2 k ≠ 2
⇒ A 1 k − 2 ; 0 ⇒ O A = 1 k − 2
S Δ A O B = 1 2 O A . O B = 1 ⇔ 1 2 .1. 1 k − 2 = 1 ⇔ | k − 2 | = 1 2 ⇔ k = 5 2 k = 3 2 (tmdk)
Đáp án cần chọn là: D