Cho (O) và một điểm M nằm ngoài đường tròn. Qua M kẻ hai đường thẳng, một đường cắt (O) tại A,B; đường còn lại cắt (O) tại C,D. c/m MA.MB=MC.MD

Những câu hỏi liên quan
Cho đường tròn tâm O ,một điểm M nằm ngoài đường tròn.Từ M kẻ đường thẳng đi qua tâm O,cắt đường tròn tại hai điểm A,B (A nằm giữa M và B).Kẻ đường thẳng thứ hai đi qua M,cắt đường tròn tại hai điểm phân biệt C,D (C nằm giữa M và D. C khác A).ĐƯờng thẳng vuông góc với MA tại M cắt đường thẳng BC tại N,đường thẳng NA cắt đường tròn tại điểm thứ 2 là E.a.Chứng minh tứ giác AMNC nội tiếpb.Chứng minh DE vuông góc với MB
Đọc tiếp
Cho đường tròn tâm O ,một điểm M nằm ngoài đường tròn.Từ M kẻ đường thẳng đi qua tâm O,cắt đường tròn tại hai điểm A,B (A nằm giữa M và B).Kẻ đường thẳng thứ hai đi qua M,cắt đường tròn tại hai điểm phân biệt C,D (C nằm giữa M và D. C khác A).ĐƯờng thẳng vuông góc với MA tại M cắt đường thẳng BC tại N,đường thẳng NA cắt đường tròn tại điểm thứ 2 là E.
a.Chứng minh tứ giác AMNC nội tiếp
b.Chứng minh DE vuông góc với MB
a: góc ACB=1/2*sđ cung AB=90 độ
=>ΔACN vuông cân tại C
góc ACN+góc AMN=180 độ
=>AMNC nội tiếp
b: AMNC nội tiếp
=>góc CNA=góc CMA=góc BMD
góc BNE=1/2(sđ cung BE-sđ cung AC)
góc DMB=1/2*(sđ cung BD-sđ cung AC)
=>sđ cung BD=sđ cung BE
=>B nằm trên trung trực của DE
Xét ΔADB và ΔAEB có
góc ADB=góc aEB
AB chung
DB=BE
=>ΔABD=ΔAEB
=>AD=AE
=>A nằm trên trung trực của DE
=>AB là trung trực của DE
=>DE vuông góc AB
Đúng 0
Bình luận (0)
Cho (O;R) và điểm A nằm ngoài đường tròn (O). Qua A vẽ tiếp tuyến AB tiếp xúc với đường tròn (O) tại B. Vẽ một đường thẳng qua A cắt đường tròn tại hai điểm M và N ( M nằm giữa A và N). Qua M kẻ đường thẳng song song với AB cắt BN tại E. Gọi I là trung điểm của ME. Vẽ dây BQ của đường tròn (O) sao cho BQ đi qua điểm Ia) Chứng minh hai tam giác BMI và tam giác BQM đồng dạngb)Chứng minh tứ giác QIEN nội tiếpc) Chứng minh BM.QNBN.MQ
Đọc tiếp
Cho (O;R) và điểm A nằm ngoài đường tròn (O). Qua A vẽ tiếp tuyến AB tiếp xúc với đường tròn (O) tại B. Vẽ một đường thẳng qua A cắt đường tròn tại hai điểm M và N ( M nằm giữa A và N). Qua M kẻ đường thẳng song song với AB cắt BN tại E. Gọi I là trung điểm của ME. Vẽ dây BQ của đường tròn (O) sao cho BQ đi qua điểm I
a) Chứng minh hai tam giác BMI và tam giác BQM đồng dạng
b)Chứng minh tứ giác QIEN nội tiếp
c) Chứng minh BM.QN=BN.MQ
Cho đường tròn (O;R) và một điểm A nằm ngoài đường tròn. Kẻ một đường thẳng qua A và không đi qua tâm O, cắt đường tròn tại 2 điểm phân biệt M, N (M nằm giữa A và N). Từ A vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là hai tiếp điểm). Đường thẳng BC cắt AO tại H. Gọi I là trung điểm của MN.a) Chứng minh tứ giác ACOI là tứ giác nội tiếp.b) Chứng minh OI.OE OH.OA AC2.c) Tính theo R độ dài của OA biết diện tích của tứ giác ABOC bằng 3R2.b bic làm bài này hok zgiúp mik vs ạ
Đọc tiếp
Cho đường tròn (O;R) và một điểm A nằm ngoài đường tròn. Kẻ một đường thẳng qua A và không đi qua tâm O, cắt đường tròn tại 2 điểm phân biệt M, N (M nằm giữa A và N). Từ A vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là hai tiếp điểm). Đường thẳng BC cắt AO tại H. Gọi I là trung điểm của MN.
a) Chứng minh tứ giác ACOI là tứ giác nội tiếp.
b) Chứng minh OI.OE = OH.OA = AC2.
c) Tính theo R độ dài của OA biết diện tích của tứ giác ABOC bằng 3R2.
b bic làm bài này hok z
giúp mik vs ạ
cho đường tròn o r và điểm m nằm ngoài đường tròn .qua m kẻ hai tiếp tuyến ma,mb với đường tròn (0,r) (a,b là tiếp điểm ) đoạn thẳng om cắt đường thẳng ab tại điểm h và cắt đường tròn (0,r) tại I 1, chứng minh M,A,B,O cùng thuộc một đường tròn 2,kẻ đường kính A,B của đường tròn (O,R) Đoạn thẳng MD cắt đường tròn (O,R) tại C khác D chứng minh MA² =MH.MO=MC.MD
Mình làm tắt nha bạn không hiểu đâu thì hỏi lại nhé
a) MA, MB là tiếp tuyến
=> \(\widehat{OBM}=\widehat{OAM}=90^o\) (t/c tiếp tuyến)
=> \(\widehat{OBM}+\widehat{OAM}=180^o\)
mà 2 góc đối nhau
=> tứ giác AOBM nội tiếp
=> 4 điểm A, O, B, M cùng thuộc 1 đường tròn
b) Áp dụng hệ thức lượng vào tam giác OAM vuông tại A đường cao AH
=> \(AM^2=MH.MO\)
Áp dụng hệ thức lượng vào tam giác DAM vuông tại A đường cao AC
=> \(AM^2=MC.MD\)
=> \(AM^2=MH.MO=MC.MD\)
Đúng 1
Bình luận (0)
Cho đường tròn (O; R) và một điểm M cố định nằm ngoài đường tròn (O). Từ M kẻ các tiếp tuyến MA, MB tới (O) (A, B là các tiếp điểm). MO cắt AB tại H. Một đường thẳng d thay đổi đi qua M nhưng không đi qua O cắt đường tròn (O) tại hai điểm N, P (N nằm giữa M và P). Gọi I là trung điểm của NP.a) Chứng minh bốn điểm M, A, I, O cùng thuộc một đường tròn.b) Qua B kẻ đường thẳng song song với MO và cắt đường tròn (O) tại D. Chứng minh và AD là đường kính của (O).c) Tiếp tuyến của (O) tại N và P cắt...
Đọc tiếp
Cho đường tròn (O; R) và một điểm M cố định nằm ngoài đường tròn (O). Từ M kẻ các tiếp tuyến MA, MB tới (O) (A, B là các tiếp điểm). MO cắt AB tại H. Một đường thẳng d thay đổi đi qua M nhưng không đi qua O cắt đường tròn (O) tại hai điểm N, P (N nằm giữa M và P). Gọi I là trung điểm của NP.
a) Chứng minh bốn điểm M, A, I, O cùng thuộc một đường tròn.
b) Qua B kẻ đường thẳng song song với MO và cắt đường tròn (O) tại D. Chứng minh ![]() và AD là đường kính của (O).
và AD là đường kính của (O).
c) Tiếp tuyến của (O) tại N và P cắt nhau tại F. Chứng minh ![]() đồng dạng
đồng dạng ![]() và điểm F chuyển động trên một đường thẳng cố định khi đường thẳng d quay quanh M mà vẫn thỏa mãn các yêu cầu đề bài.
và điểm F chuyển động trên một đường thẳng cố định khi đường thẳng d quay quanh M mà vẫn thỏa mãn các yêu cầu đề bài.
Câu a),b) tự làm nhé , mình chỉ giúp câu c) thôi .
OI vuông góc NP ( Do I là trung điểm của MP ) , OF vuông góc NP ( Do OF là đường trung trực của NP )
=> O,I,F thẳng hàng
Tam giác ONF vuông tại N , đường cao NI
=> ON^2 = OI.OF
Mà ON=OA
OA^2 = OH.OM
=> OH.OM=OI.OF
=> OH/OI=OF/OM
Xét tam giác OIM và tam giác OHF có
góc MOF chung
OH/OI=OF/OM
=> Tam giác OIM đồng dạng tam giác OHF
=> góc OHF=góc OIM (=90 độ )
OH vuông HF
mà OH vuông AB
=> A,B,F thẳng hàng
=> F nằm trên đường thẳng cố định AB khi đường thẳng d quay quanh M mà vẫn thỏa mãn các yêu cầu đề bài
Điều phải chứng minh
Đúng 0
Bình luận (0)
Kẻ hộ mk hình Cho đường tròn (O; R) và điểm A cố định nằm ngoài đường tròn. Một đường thẳng d đi qua A cắt đường tròn (O; R) tại B và C (BC không đi qua O, B nằm giữa A và C). Từ A kẻ các tiếp tuyến AM, AN tới đường tròn (M, N là hai tiếp điểm, M thuộc mặt phẳng bờ AC có chứa điểm O), gọi H là trung điểm của BC.
Cho đường tròn (O;R) và một điểm S nằm bên ngoài đường tròn. Kẻ các tiếp tuyến SA,SB của đường tròn (O;R) (với A,B là tiếp điểm). Đường thẳng a đi qua S (không đi qua tâm O) cắt đường tròn(O;R) tại hai điểm M,N (M nằm giữ S và N). a) CM: SO ⊥ AB b) Gọi I là trung điểm của MN và H là giao điểm của SO,AB ;hai đường...
Đọc tiếp
Cho đường tròn (O;R) và một điểm S nằm bên ngoài đường tròn. Kẻ các tiếp tuyến SA,SB của đường tròn (O;R) (với A,B là tiếp điểm). Đường thẳng a đi qua S (không đi qua tâm O) cắt đường tròn(O;R) tại hai điểm M,N (M nằm giữ S và N). a) CM: SO ⊥ AB b) Gọi I là trung điểm của MN và H là giao điểm của SO,AB ;hai đường thẳng OI và AB cắt nahu tại E.CM: OI.OE=R2 (vẽ hộ em hình luôn ạ)
a, Ta có SA = SB (tc tiếp tuyến cắt nhau )
OA = OB = R
Vậy OS là đường trung trực đoạn AB
=> SO vuông AB tại H
b, Vì I là trung điểm
=> OI vuông NS
Xét tứ giác IHSE ta có ^EHS = ^EIS = 900
mà 2 góc này kề, cùng nhìn cạnh ES
Vậy tứ giác IHSE nt 1 đường tròn
=> ^ESH = ^HIO ( góc ngoài đỉnh I )
Xét tam giác OIH và tam giác OSE có
^HIO = ^OSE (cmt)
^O_ chung
Vậy tam giác OIH ~ tam giác OSE (g.g)
\(\dfrac{OI}{OS}=\dfrac{OH}{OE}\Rightarrow OI.OE=OH.OS\)
Xét tam giác OAS vuông tại A ( do SA là tiếp tuyến với A là tiếp điểm), đường cao AH ta có
\(OA^2=OH.OS\)(hệ thức lượng)
\(\Rightarrow OA^2=R^2=OI.OE\)
Đúng 3
Bình luận (0)
Cho đường tròn (O) và một điểm M cố định không nằm trên đường tròn. Qua M kẻ hai đường thẳng . Đường thẳng thứ nhất cắt (O) tại A và B. Đường thẳng thứ hai cắt (O) tại C và D. Chứng minh MA.MB = MC.MD.
Hướng dẫn: Xét cả hai trường hợp điểm M nằm bên trong và bên ngoài đường tròn. Trong mỗi trường hợp, xét hai tam giác đồng dạng.
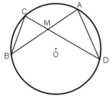
TH1: M nằm trong đường tròn.
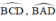 là hai góc nội tiếp cùng chắn cung
là hai góc nội tiếp cùng chắn cung 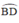
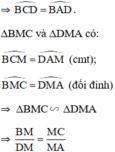
⇒ MA.MB = MC.MD
TH2: M nằm ngoài đường tròn.
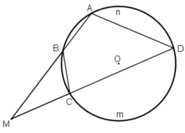
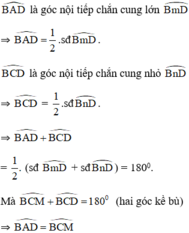
ΔMBC và ΔMDA có:
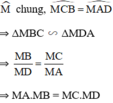
Kiến thức áp dụng
+ Góc nội tiếp chắn một cung có số đo bằng một nửa số đo của cung đó.
+ Hai góc nội tiếp chắn cùng một cung thì có số đo bằng nhau.
Đúng 0
Bình luận (0)
Cho đường tròn (O) và một điểm M cố định không nằm trên đường tròn. Qua M kẻ hai đường thẳng . Đường thẳng thứ nhất cắt (O) tại A và B. Đường thẳng thứ hai cắt (O) tại C và D. Chứng minh MA.MB = MC.MD.
Hướng dẫn: Xét cả hai trường hợp điểm M nằm bên trong và bên ngoài đường tròn. Trong mỗi trường hợp, xét hai tam giác đồng dạng.
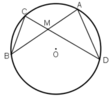
TH1: M nằm trong đường tròn.
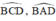 là hai góc nội tiếp cùng chắn cung
là hai góc nội tiếp cùng chắn cung 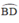
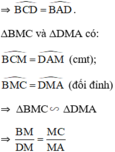
⇒ MA.MB = MC.MD
TH2: M nằm ngoài đường tròn.
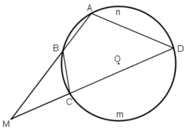
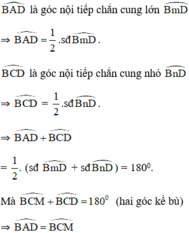
ΔMBC và ΔMDA có:
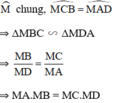
Đúng 1
Bình luận (0)

















