GIẢI PT NÀY GIÚP MIK VS: >.<
1) /x2 - 1/ + /x + 2/ = 6
2) / x2 + 2x/ + / 3x2 + 6x + 3/ = 1
Giải giúp mik bài này bằng cách lập pt vs ạ 
bạn chịu khó đánh máy ra đc không? Chứ khó nhìn đề lắm
\(8(x+\dfrac{1}{x} )^{2} \)\(+4(x^{2}+\dfrac{1}{x^{2} } )^{2}\)\(-4 (x^{2}+\dfrac{1}{x^{2}} )(x+\dfrac{1}{x})^{2} \)\(=(x+4)^{2}\)
giúp mik vs ạ cho mik cách giải pt này vs ạ
=>8(x+1/x)^2+4[(x+1/x)^2-2]^2-4[(x+1/x)^2-2](x+1/x)^2=(x+4)^2
Đặt x+1/x=a(a>=2)
=>8a^2+4[a^2-2]^2-4[a^2-2]*a^2=(x+4)^2
=>8a^2+4a^4-16a^2+16-4a^4+8a^2=(x+4)^2
=>(x+4)^2=16
=>x+4=4 hoặc x+4=-4
=>x=-8;x=0
Điều kiện: \(x\ne0\)
\(\Leftrightarrow8\left(x+\dfrac{1}{x}\right)^2+4\left(x^2+\dfrac{1}{x^2}\right)\left[\left(x^2+\dfrac{1}{x^2}\right)-\left(x+\dfrac{1}{x}\right)^2\right]=\left(x+4\right)^2\)
\(\Leftrightarrow8\left(x+\dfrac{1}{x}\right)^2-8\left(x^2+\dfrac{1}{x^2}\right)=\left(x+4\right)^2\\ \Leftrightarrow\left(x+4\right)^2=16\\ \Rightarrow\left\{{}\begin{matrix}x=0\\x=-8\end{matrix}\right.\)
Vì \(x\ne0\) nên \(S=\left\{-8\right\}\)
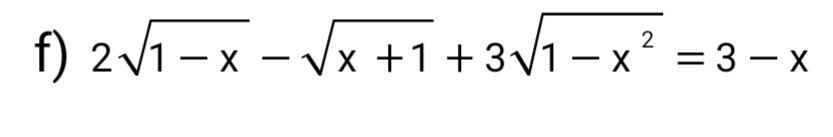 Giải pt . Mn giúp mik vs
Giải pt . Mn giúp mik vs
ĐK: \(-1\le x\le1\)
Đặt \(\sqrt{1-x}=a;\sqrt{x+1}=b\Rightarrow3-x=2a^2+b^2\)
\(pt\Leftrightarrow2a-b+3ab=2a^2+b^2\)
\(\Leftrightarrow2a^2+b^2-2a+b-3ab=0\)
\(\Leftrightarrow2a^2-a\left(3b+2\right)+b^2+b=0\)
\(\Delta=\left(3b+2\right)^2-4.2.\left(b^2+b\right)=9b^2+12b+4-8b^2-8b\)
\(=b^2+4b+4=\left(b+2\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}a=\dfrac{3b+2-\left(b+2\right)}{4}=\dfrac{2b}{4}=\dfrac{b}{2}\Leftrightarrow2a=b\left(1\right)\\a=\dfrac{3b+2+b+2}{4}=\dfrac{4b+4}{4}=b+1\left(2\right)\end{matrix}\right.\)
pt (1) \(\Leftrightarrow2\sqrt{1-x}=\sqrt{x+1}\)
\(\Leftrightarrow4\left(1-x\right)=x+1\)
\(\Leftrightarrow5x=3\Leftrightarrow x=\dfrac{5}{3}\left(tm\right)\)
\(pt\left(2\right)\Leftrightarrow\sqrt{1-x}=1+\sqrt{x+1}\)
\(\Leftrightarrow1-x=1+x+1+2\sqrt{x+1}\)
\(\Leftrightarrow-1-2x=2\sqrt{x+1}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-\dfrac{1}{2}\\4x^2+4x+1=4x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le-\dfrac{1}{2}\\4x^2=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-\dfrac{1}{2}\\\left[{}\begin{matrix}x=\dfrac{\sqrt{3}}{2}\left(l\right)\\x=-\dfrac{\sqrt{3}}{2}\left(tm\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy, pt có tập nghiệm là: \(S=\left\{-\dfrac{\sqrt{3}}{2};\dfrac{5}{3}\right\}\)
bn nào đó giúp mik giải pt này vs
\(\left(x+x^2\right)\sqrt{x^2+1}=\left(x+1\right)^2\)
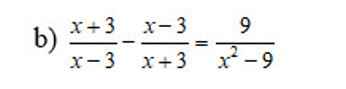
giải giúp pt này vs mn
\(\dfrac{x+3}{x-3}-\dfrac{x-3}{x+3}=\dfrac{9}{x^2-9}\left(ĐKXĐ:x\ne\pm3\right)\)
\(\Leftrightarrow\dfrac{\left(x+3\right)^2-\left(x-3\right)^2}{\left(x-3\right)\left(x+3\right)}=\dfrac{9}{\left(x-3\right)\left(x+3\right)}\)
\(\Rightarrow x^2+6x+9-x^2+6x-9=9\)
\(\Leftrightarrow12x=9\)
\(\Leftrightarrow x=\dfrac{3}{4}\) (nhận).
Vậy \(S=\left\{\dfrac{3}{4}\right\}\)
Giải pt :
x/40 - x/50 = 1/3
giải hộ mik vs
MIK ĐANG VỘI LẮM! GIÚP MIK VS
Bài này quá dễ
x/40 - x/50= 1/3
<=>5x/200 - 4x/200=1/3
<=> x/200= 1/3
<=> x= 200/3.
bạn ê, mik bị ngu toán, lười suy nghĩ ấy mà nên đừng nói dễ hay khó j vs mik
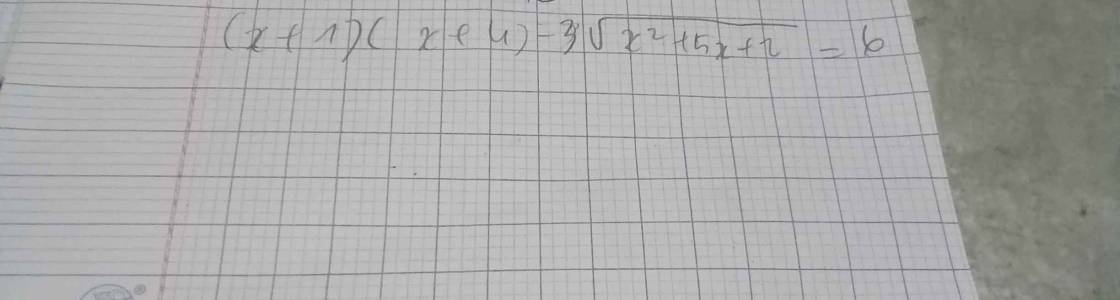 giải pt này giúp e vs ạ
giải pt này giúp e vs ạ
ĐKXĐ: \(x^2+5x+2>=0\)
=>\(\left[{}\begin{matrix}x>=\dfrac{-5+\sqrt{17}}{2}\\x< =\dfrac{-5-\sqrt{17}}{2}\end{matrix}\right.\)
\(\left(x+1\right)\left(x+4\right)-3\sqrt{x^2+5x+2}=6\)
=>\(x^2+5x+4-3\sqrt{x^2+5x+2}-6=0\)
=>\(x^2+5x+2-3\sqrt{x^2+5x+2}-4=0\)(1)
Đặt \(\sqrt{x^2+5x+2}=a\)(a>=0)
Phương trình (1) trở thành:
\(a^2-3a-4=0\)
=>(a-4)(a+1)=0
=>\(\left[{}\begin{matrix}a=4\left(nhận\right)\\a=-1\left(loại\right)\end{matrix}\right.\)
=>\(x^2+5x+2=4^2=16\)
=>\(x^2+5x-14=0\)
=>\(\left(x+7\right)\left(x-2\right)=0\)
=>\(\left[{}\begin{matrix}x=-7\left(nhận\right)\\x=2\left(nhận\right)\end{matrix}\right.\)
giải chi tiết giúp mik nha, vt hẳn pt ra vs ạ

Giúp mik câu này vs giải thik gium mik vs
/ 2x - 3 / = 3 - 2x
Các bạn ơi giải giúp mik bài này vs ạ! Đáp án của bài này là S = {x ∈ R / x =< 3/2} mà mik ko biết cách giải ạ! Ai biết giúp mik vs! Thanks nhiều!
\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)