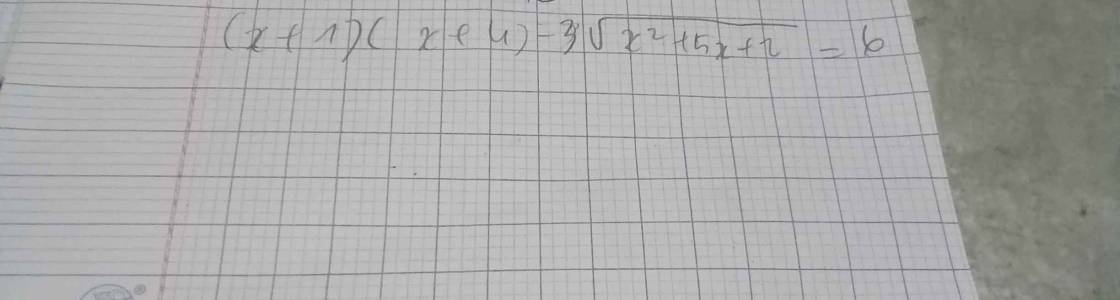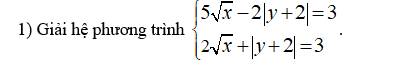ĐKXĐ: \(x^2+5x+2>=0\)
=>\(\left[{}\begin{matrix}x>=\dfrac{-5+\sqrt{17}}{2}\\x< =\dfrac{-5-\sqrt{17}}{2}\end{matrix}\right.\)
\(\left(x+1\right)\left(x+4\right)-3\sqrt{x^2+5x+2}=6\)
=>\(x^2+5x+4-3\sqrt{x^2+5x+2}-6=0\)
=>\(x^2+5x+2-3\sqrt{x^2+5x+2}-4=0\)(1)
Đặt \(\sqrt{x^2+5x+2}=a\)(a>=0)
Phương trình (1) trở thành:
\(a^2-3a-4=0\)
=>(a-4)(a+1)=0
=>\(\left[{}\begin{matrix}a=4\left(nhận\right)\\a=-1\left(loại\right)\end{matrix}\right.\)
=>\(x^2+5x+2=4^2=16\)
=>\(x^2+5x-14=0\)
=>\(\left(x+7\right)\left(x-2\right)=0\)
=>\(\left[{}\begin{matrix}x=-7\left(nhận\right)\\x=2\left(nhận\right)\end{matrix}\right.\)