cho tam giác vuông MNP tại M, đường cao MK. Biết MN= 7cm, NP= 25cm. Tính MP, MK, NK

Những câu hỏi liên quan
Cho tam giác MNP vuông tại M; đường cao MK. Biết MN=7cm; NP=25cm.
a) Tính MP,MK,NK.
b) Gọi D là hình chiếu của K trên MN, E là hình chiếu của K trên MP. Chứng minh: MD.MN=ME.MP
c) Chứng minh: KD.MN+KE.MP=MN.MP
~GIẢI GIÚP MIK ĐI Ạ~
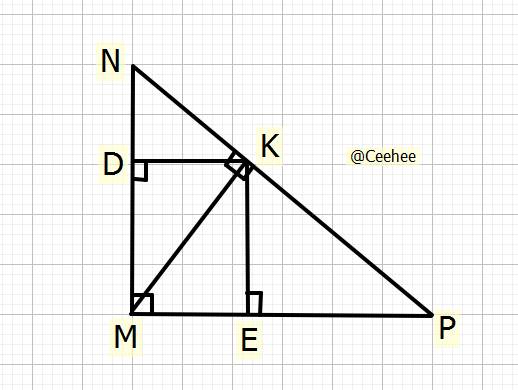
`a)` Biết `MN=7cm;NP=25cm`
Xét \(\Delta MNP\) vuông tại `M`, đường cao `MK`
Ta có: \(NP^2=MN^2+MP^2\) (đl Pytago)
\(\Rightarrow25^2=7^2+MP^2\\ \Rightarrow MP^2=25^2-7^2=576\\ \Rightarrow MP=\sqrt{576}=24cm\)
Ta có: \(\dfrac{1}{MK^2}=\dfrac{1}{MN^2}+\dfrac{1}{MP^2}\left(htl\right)\)
\(\Rightarrow\dfrac{1}{MK^2}=\dfrac{1}{7^2}+\dfrac{1}{24^2}\\ \Rightarrow\dfrac{1}{MK^2}=\dfrac{625}{28224}\\ \Rightarrow MK^2=\dfrac{1\cdot28224}{625}\\ \Rightarrow MK=\sqrt{\dfrac{28224}{625}}\\ \Rightarrow MK=6,72cm\)
Ta có: \(MN^2=NK\cdot NP\left(htl\right)\)
\(\Rightarrow7^2=NK\cdot25\\ \Rightarrow NK=\dfrac{7^2}{25}=1,96cm\)
Vậy: \(MP=24cm;MK=6,72cm;NK=1,96cm\)
`b)` \(C/m:MD\cdot MN=ME\cdot MP\)
Xét \(\Delta KMN\) vuông tại `K`
Ta có: \(MK^2=MD\cdot MN\left(htl\right)\left(1\right)\)
Xét \(\Delta KMP\) vuông tại `K`
Ta có: \(MK^2=ME\cdot MP\left(htl\right)\left(2\right)\)
Từ `(1)` và `(2)` \(\Rightarrow MK^2=MK^2\)
\(\Rightarrow MD\cdot MN=ME\cdot MP\left(=MK^2\right)\)
(Câu `c)` tớ chịu :v).
Đúng 2
Bình luận (2)
Bài 1: Cho tam giác MNP vuông tại M, đưrờng cao MK. Biết MN 15cm, MK 12cm. al Chứng minh AMKN SAPMN b/ Tính độ dài các đoạn thắng NK, MP, NP. c/ Chứng minh MN² KN.NP d/ Trên cạnh MP lấy điểm A sao cho PA 5 cm, trên cạnh NP lấy điểm C sao cho PC 4 cm. Chứng minh APAC là tam giác vuông.
Đọc tiếp
Bài 1: Cho tam giác MNP vuông tại M, đưrờng cao MK. Biết MN= 15cm, MK = 12cm.
al Chứng minh AMKN SAPMN
b/ Tính độ dài các đoạn thắng
NK, MP, NP.
c/ Chứng minh MN² = KN.NP
d/ Trên cạnh MP lấy điểm A sao cho
PA = 5 cm, trên cạnh NP lấy điểm C sao
cho PC = 4 cm. Chứng minh
APAC là tam giác vuông.
a: Xét ΔMKN vuông tại K và ΔPMN vuông tại M có
góc N chung
=>ΔMKN đồng dạng với ΔPMN
b: NK=căn 15^2-12^2=9cm
PK=12^2/9=16cm
PN=9+16=25cm
c: ΔMNP vuông tại M có MK là đường cao
nên NM^2=NK*NP
Đúng 0
Bình luận (0)
Bài tập 3: Cho tam giác MNP vuông tại M, đường cao MH (H thuộc NP). Biết MN 10cm, NH 7cm. Tính NP, MP và SinHMP
Đọc tiếp
Bài tập 3: Cho tam giác MNP vuông tại M, đường cao MH (H thuộc NP). Biết MN = 10cm,
NH = 7cm. Tính NP, MP và SinHMP
Xét ΔMNP vuông tại M có MH là đường caop
nên \(NM^2=NH\cdot NP\)
=>\(NP\cdot7=10^2=100\)
=>\(NP=\dfrac{100}{7}\left(cm\right)\)
ΔMNP vuông tại M
=>\(MN^2+MP^2=NP^2\)
=>\(MP^2=NP^2-MN^2=\left(\dfrac{100}{7}\right)^2-10^2=\dfrac{5100}{49}\)
=>\(MP=\dfrac{10\sqrt{51}}{7}\left(cm\right)\)
\(\widehat{HMP}+\widehat{HMN}=90^0\)
\(\widehat{HMN}+\widehat{N}=90^0\)
=>\(\widehat{HMP}=\widehat{N}\)
Xét ΔMNP vuông tại M có \(sinN=\dfrac{MP}{NP}\)
=>\(sinHMP=\dfrac{10\sqrt{51}}{7}:\dfrac{100}{7}=\dfrac{\sqrt{51}}{10}\)
Đúng 0
Bình luận (0)
cho tam giác MNP vuông tại M kẻ đường cao MH, đường phân giác MK của góc HMP, kẻ đường cao KE vuông góc MP tại E. tính MN biết NP=12cm, KE=3cm
Cho tam giác MNP vuông tại M (MN<MP). Vẽ đường cao MH(H thuộc NP)
a. Chứng minh tam giác MNP đồng dạng với tam giác HNM
b. Chứng minh MN^2=NH.NP
c. Vẽ tia phân giác MK của góc NMP (K thuộc NP). Biết MN=7,2 cm và MP=9,6 cm. Tính độ dài các đoạn thẳng NP, NH và MK.
tự vẽ hình nhé
a, Xét \(\Delta\) MNP và \(\Delta\) HNM
< MNP chung
<NMP=<NHM(=90\(^0\) )
b,=> \(\dfrac{MN}{HN}=\dfrac{NP}{MN}\)
=> \(MN^2=NP\cdot NH\)
c, xét \(\Delta\) NMP vg tại M, áp dụng định lí Py - ta - go trong tam giác vg có
\(MN^2+MP^2=NP^2\)
=> \(NP^2=144\Rightarrow NP=12cm\)
Ta có \(MN^2=NH\cdot NP\)
Thay số:\(7,2^2=NH\cdot12\Rightarrow NH=4,32cm\)
Đúng 2
Bình luận (1)
Mình nghĩ MK nên áp dụng ta lét nhé
7,2/x = 12/9,6-x
<=>7,2 . (9.6-x) = 12.x
<=>69,12 - 7,2x = 12x
<=>69,12 = 12x + 7,2x
<=> 69,12 = 19, 2
<=> x = 69,12 : 19,2 = 3,6
Vậy MK bằng 3,6cm
(mình ko chắc đúng ko nhưng theo mình là vậy)
Đúng 0
Bình luận (0)
Cho tam giác MNP vuông tại M, có MN = 8cm, NP = 15cm. Kẻ MK vuông
góc với NP tại K. Tính độ dài các đoạn thẳng: MP, MK, NK, KP.
Cho tam giác MNP vuông tại M , đường cao MA=7cm . Biết AP = 4,5 cm a, tính góc P b, Tính độ dài các cạnh MN, MP,AN, NP
a: Xét ΔMAP vuông tại P có \(tanP=\dfrac{MA}{AP}=\dfrac{7}{4,5}=\dfrac{14}{9}\)
=>\(\widehat{P}\simeq57^0\)
b: Xét ΔMNP vuông tại M có MA là đường cao
nên \(MA^2=AN\cdot AP\)
=>\(AN\cdot4,5=7^2=49\)
=>\(AN=\dfrac{98}{9}\left(cm\right)\)
NP=NA+AP
\(=\dfrac{98}{9}+\dfrac{9}{2}=\dfrac{277}{18}\left(cm\right)\)
Xét ΔMNP vuông tại M có MA là đường cao
nên \(\left\{{}\begin{matrix}MN^2=NA\cdot NP\\MP^2=PA\cdot PN\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}MN=\sqrt{\dfrac{98}{9}\cdot\dfrac{277}{18}}=\dfrac{7\sqrt{277}}{9}\left(cm\right)\\MP=\sqrt{4,5\cdot\dfrac{277}{18}}=\dfrac{\sqrt{277}}{2}\left(cm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho tam giác MNP vuông tại M có MN=8cm, MP=15cm, đường cao MK, vẽ KE vuông góc với MN( E thuộc MN), KF vuông góc với MP(F thuộc MP).
a, Tính NP , MK?
b, tứ giác MEKF là hình gì? vì sao? tính EF?
c, C/M: ME.MN = MF.MP?
a: NP=căn 8^2+15^2=17cm
MK=8*15/17=120/17cm
b: góc MEK=góc MFK=góc FME=90 độ
=>MEKF là hình chữ nhật
=>MK=EF=120/17cm
c: ΔMKN vuông tại K có KE là đường cao
nên ME*MN=MK^2
ΔMKP vuông tại K có KF là đường cao
nên MF*MP=MK^2
=>ME*MN=MF*MP
Đúng 0
Bình luận (0)
cho tam giác MNP vuông tại M có MK đường cao.biết MP = 10 cm, KP = 8 cm .Tính MK, NK, MN
Xem chi tiết
Áp dụng hệ thức trong tam giác vuông có:
\(MP^2=PK.PN\Leftrightarrow PN=12,5\left(cm\right)\)
\(MN=\sqrt{PN^2-MP^2}=7,5cm\)
\(MN^2=NK.NP\Leftrightarrow NK=4,5\left(cm\right)\)
\(MK^2=KN.KP=4,5.8=36\Leftrightarrow MK=6\left(cm\right)\)
Vậy...
Đúng 1
Bình luận (0)
NP=MP^2/PN=10^2/8=12,5cm
MK=căn 10^2-8^2=6cm
NK=6^2/8=4,5cm
MN=căn 12,5^2-10^2=7,5cm
Đúng 0
Bình luận (0)
`@`Phamdanhv.
ảnh mình không tải được , bạn vào link này nhé
`=>`
blob:https://www.facebook.com/87ade4e1-6c0b-45ee-b42f-df163ba3224e
Đúng 0
Bình luận (0)


















