nếu tam giác MNP vuông tại M thì cosN bằng
NẾU TAM GIÁC MNP VUÔNG TẠI M THÌ TAN P=
NẾU TAM GIÁC MNP VUÔNG TẠI M VÀ MN=1,5CM ,SIN P= \(\dfrac{5}{13}\) THÌ ĐỘ DÀI CẠNH NP BẰNG
CHỈ CÁCH TÍCH HOẶC COONGTHUWCS GIÚP MK
\(tanP=\dfrac{MN}{MP}\)
\(sinP=\dfrac{MN}{NP}\Rightarrow NP=\dfrac{MN}{sinP}=\dfrac{1,5}{\dfrac{5}{13}}=3,9\left(cm\right)\)
Cho tam giác MNP vuông tại M, đường cao MH. Biết NH=1cm; PH=4cm a) Tính độ dài các đoạn thẳng MH; MP b)Tính cosN; tan P c)Lấy A là điểm bất kì trên cạnh MP (A≠M; A≠P). Gọi K là hình chiếu của M trên NA. Chứng minh rằng: Tam giác NKP đồng dạng với NHA d)Đường thẳng d qua A song song với NP cắt MN tại B. Giao điểm của AN và BP là O. Tia Ax song song với MN cắt BP tại F. Tia By song song với MP cắt NA tại E. Chứng minh rằng AB^2=EF.NP
a: NP=NH+HP
=1+4
=5(cm)
Xét ΔMNP vuông tại M có MH là đường cao
nên \(MH^2=HN\cdot HP\)
=>\(MH^2=1\cdot4=4\)
=>MH=2(cm)
ΔMHP vuông tại H
=>\(HM^2+HP^2=MP^2\)
=>\(MP^2=2^2+4^2=20\)
=>\(MP=2\sqrt{5}\left(cm\right)\)
b:
ΔMNP vuông tại M
=>\(MN^2+MP^2=NP^2\)
=>\(MN^2+\left(2\sqrt{5}\right)^2=5^2\)
=>\(MN^2=25-20=5\)
=>\(MN=\sqrt{5}\left(cm\right)\)
Xét ΔMNP vuông tại M có \(cosN=\dfrac{MN}{NP}\)
=>\(cosN=\dfrac{\sqrt{5}}{5}\)
Xét ΔMNP vuông tại M có \(tanP=\dfrac{MN}{MP}\)
=>\(tanP=\dfrac{\sqrt{5}}{2\sqrt{5}}=\dfrac{1}{2}\)
c: Xét ΔMNA vuông tại M có MK là đường cao
nên \(NK\cdot NA=NM^2\left(1\right)\)
Xét ΔMNP vuông tại M có MH là đường cao
nên \(NH\cdot NP=NM^2\left(2\right)\)
Từ (1) và (2) suy ra \(NK\cdot NA=NH\cdot NP\)
=>\(\dfrac{NK}{NH}=\dfrac{NP}{NA}\)
Xét ΔNKP và ΔNHA có
\(\dfrac{NK}{NH}=\dfrac{NP}{NA}\)
\(\widehat{KNP}\) chung
Do đó: ΔNKP đồng dạng với ΔNHA
Câu 1. Cho tam giác MNP cân tại M, nếu góc M=50độ thì góc ở đáy bằng
A. 130 độ
B. 40 độ
C. 100 độ
D. 65 độ
Câu 2. Cho tam giác MNP vuông tại M, theo định lý Pytago ta có:
A. NM2=MP2+NP2
B. NP2=MN2+MP2
C. MP2=MN2+NP2
D. NP2=MN2-MP2
Câu 3. Nếu tam giác ABC có AC>AB thì theo quan hệ giữa góc và cạnh đối diện trong tam giác
A. Góc A> góc B
B. Góc A> góc C
C. Góc C> góc A
D. Góc B> góc C
Câu 1. Cho tam giác MNP cân tại M, nếu góc M=50độ thì góc ở đáy bằng
A. 130 độ
B. 40 độ
C. 100 độ
D. 65 độ
Câu 2. Cho tam giác MNP vuông tại M, theo định lý Pytago ta có:
A. NM2=MP2+NP2
B. NP2=MN2+MP2
C. MP2=MN2+NP2
D. NP2=MN2-MP2
Câu 3. Nếu tam giác ABC có AC>AB thì theo quan hệ giữa góc và cạnh đối diện trong tam giác
A. Góc A> góc B
B. Góc A> góc C
C. Góc C> góc A
D. Góc B> góc C
Tam giác MNP vuông tại M thì sinN bằng:
Tam giác MNP có MN = NP và góc M bằng 45ᵒ, khi đó kết luận nào sau đây là đúng nhất?
Tam giác MNP vuông tại M
Tam giác MNP đều
Tam giác MNP cân tại N
Tam giác MNP vuông cân tại N
Cho tam giác ABC vuông tại A có góc B bằng 30° và tam giác MNP vuông tại góc M có góc P bằng 60°. Chứng minh tam giác ABC đồng dạng với tam giác MNP.
Ta có: <A+<B+<C=180
90+30+<C=180
<c=180-30-90=60
Xét ▲ABC và ▲MNP ta có:
<A=<M=90
<C=<P(=60)
Do đó ▲ABC đồng dạng ▲MNP(g-g)
Cho tam giác MNP vuông tại P . Phân giác góc M cắt NP tại A . Từ A kẻ AH vuông góc với MN a CHỨNG MINH PM bằng MH b MP cắt AH tại B CHỨNG MINH tam giác MNP bằng tam giác MBH
a: Xét ΔMPA vuông tại P và ΔMHA vuông tại H có
MA chung
\(\widehat{PMA}=\widehat{HMA}\)
Do đó: ΔMPA=ΔMHA
Suy ra: MP=MH
b: Xét ΔMNP vuông tại P và ΔMBH vuông tại H có
MP=MH
\(\widehat{PMN}\) chung
Do đó: ΔMNP=ΔMBH
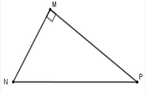
Cho tam giác MNP vuông tại M. Khi đó cos M N P ^ bằng:
A. M N N P
B. M P N P
C. M N M P
D. M P M N
Ta có: cos M N P ^ = M N N P
Đáp án cần chọn là: A
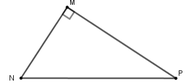
Cho tam giác MNP vuông tại M. Khi đó tan M N P ^ bằng:
A. M N N P
B. M P N P
C. M N M P
D. M P M N
Ta có: tan M N P ^ = M P M N
Đáp án cần chọn là: D