 giúp e với ạ 💦
giúp e với ạ 💦
đề: dùng hằng đẳng thức khi nhóm ý ạ
(3x+1)(3x-1)
hằng đẳng thức ai giúp e với ạ
(3x+1)(3x-1)
=\(\left(3x\right)^2-1^2\)
=\(9x^2-1\)
Giúp e với các anh chị lớp 8 :< Hằng đẳng thức khó quá ạ.
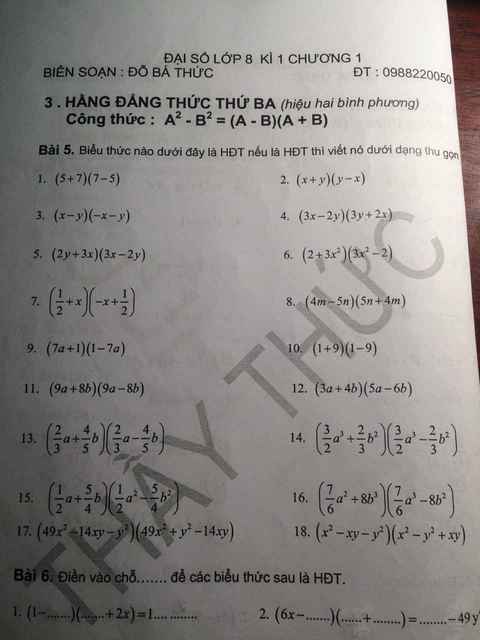
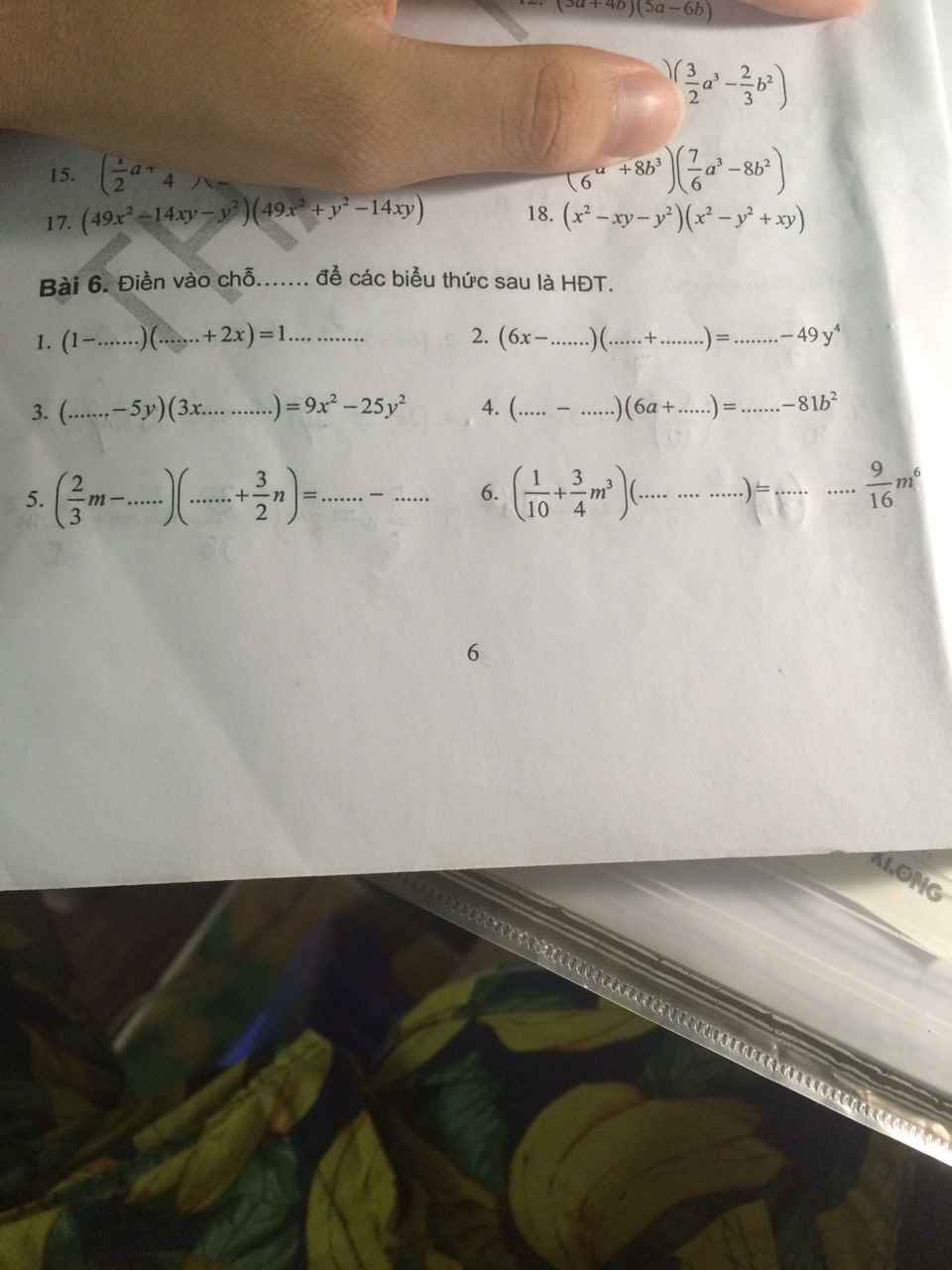
Bài 5:
1) \(\left(5+7\right)\left(7-5\right)=7^2-5^2\)
2) \(\left(x+y\right)\left(y-x\right)=y^2-x^2\)
3) \(\left(x-y\right)\left(-x-y\right)=-\left(x+y\right)\left(x-y\right)=-\left(x^2-y^2\right)=y^2-x^2\)
6) \(\left(2+3x^2\right)\left(3x^2-2\right)=9x^4-4\)
7) \(\left(\dfrac{1}{2}+x\right)\left(-x+\dfrac{1}{2}\right)=\left(\dfrac{1}{2}+x\right)\left(\dfrac{1}{2}-x\right)=\dfrac{1}{4}-x^2\)
8) \(\left(4m-5n\right)\left(5n+4m\right)=\left(4m-5n\right)\left(4m+5n\right)=16m^2-25n^2\)
9) \(\left(7a+1\right)\left(1-7a\right)=\left(1+7a\right)\left(1-7a\right)=1-49a^2\)
10) \(\left(1+9\right)\left(1-9\right)=1-9^2\)
Bài 5:
11) \(\left(9a+8b\right)\left(9a-8b\right)=81a^2-64b^2\)
13) \(\left(\dfrac{2}{3}a+\dfrac{4}{5}b\right)\cdot\left(\dfrac{2}{3}a-\dfrac{4}{5}b\right)=\dfrac{4}{9}a^2-\dfrac{16}{25}b^2\)
14) \(\left(\dfrac{3}{2}a^3+\dfrac{2}{3}b^2\right)\left(\dfrac{3}{2}a^3-\dfrac{2}{3}b^2\right)=\dfrac{9}{4}a^6-\dfrac{4}{9}b^4\)
17) \(\left(49x^2-14xy-y^2\right)\left(49x^2-14xy+y^2\right)=\left(49x^2-14xy\right)^2-y^4\)
Giúp e với ạ 💦
A
1 A
2 D
3 A
4 B
5 A
6 A
7 C
8 C
9 D
10 D
B
1 D
2 D
3 C
4 B
5 C
6 A
7 A
8 C
9 A
10 A
Đề 1 : cảm nghĩ về một món quà nhận được từ mẹ thời thơ ấu. Đề 2 : cảm nghĩ về sách mình học và đọc hằng ngày ( ghi tên sách luôn) KO CHÉP GG NHA MN😞💦 ,chọn 1 trong 2 đề ạ💦
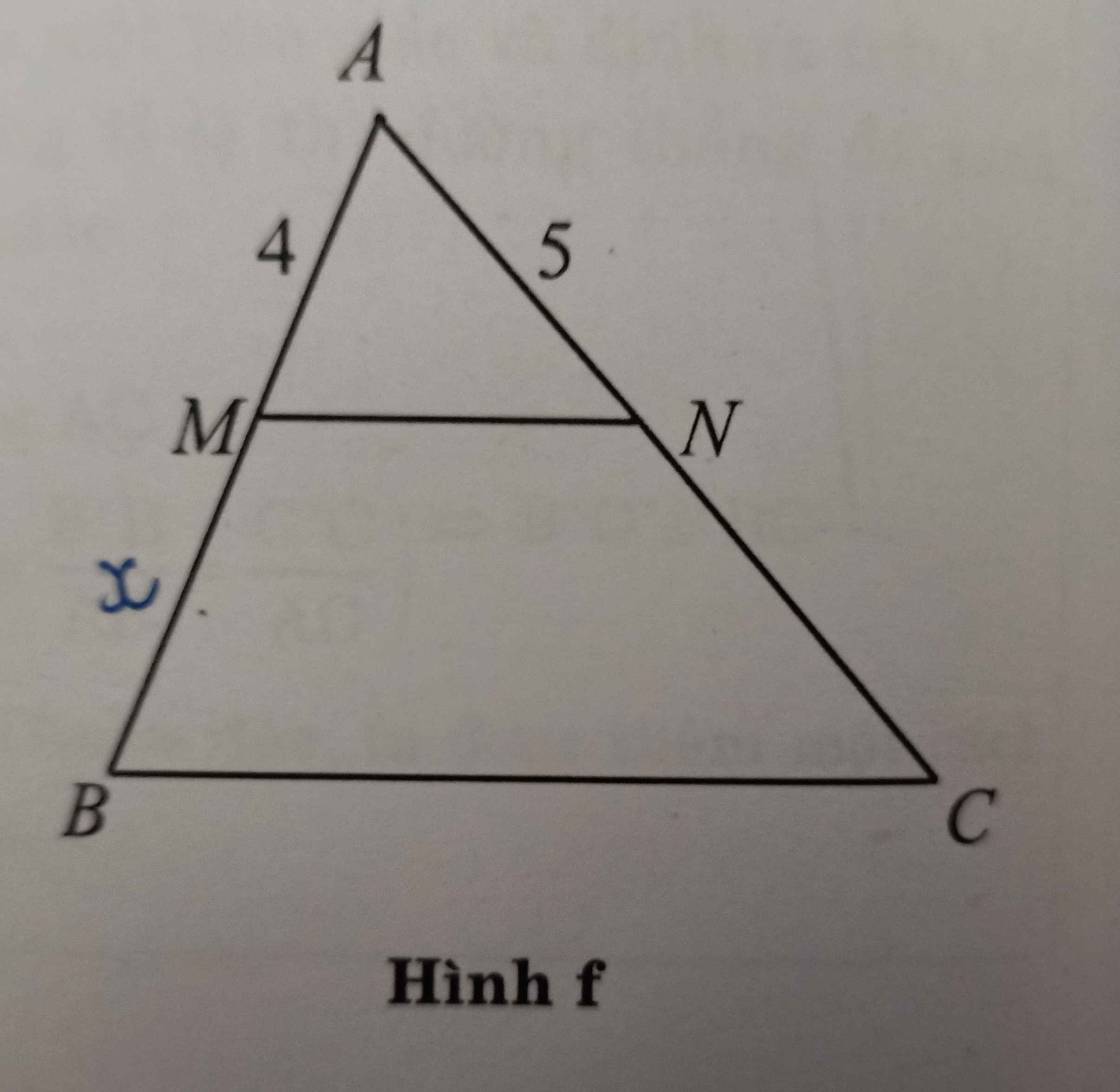
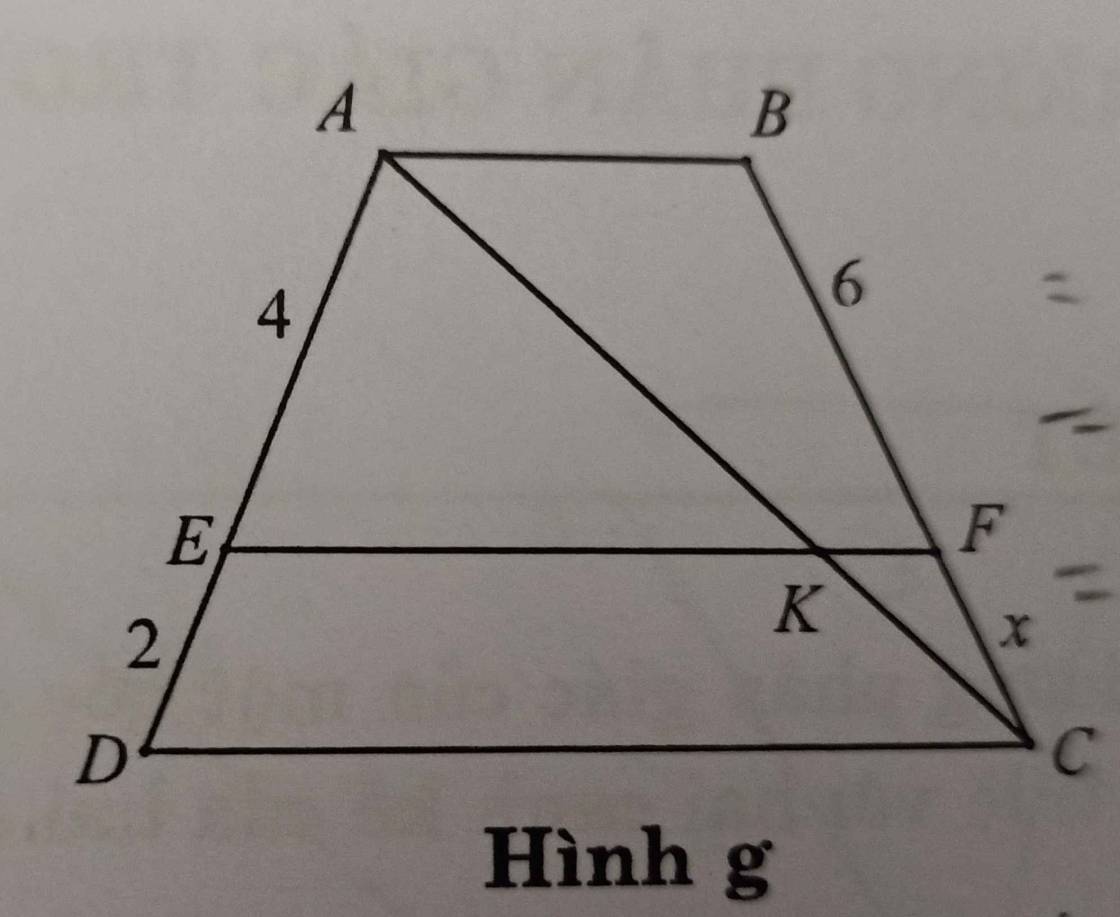 giúp e vs ạ, đề là Tính độ dài của x dùng định lý THALES ý ạ
giúp e vs ạ, đề là Tính độ dài của x dùng định lý THALES ý ạ
Hình f đề bài thiếu nên không tính được
Với hình g:
Áp dụng định lý Talet cho tam giác ADC:
\(\dfrac{AE}{ED}=\dfrac{AK}{KC}\Rightarrow\dfrac{AK}{KC}=\dfrac{4}{2}=2\)
\(\Rightarrow\dfrac{CK}{AK}=\dfrac{1}{2}\)
Áp dụng định lý Talet cho tam giác CAB:
\(\dfrac{CF}{BF}=\dfrac{CK}{AK}\Rightarrow\dfrac{x}{6}=\dfrac{1}{2}\Rightarrow x=3\)
Giải các phương trình bằng cách sử dụng các hằng đẳng thức.
Giúp với ạ!
\(\left(4A\right)\\ a,\\ \Leftrightarrow\left[\left(x-2\right)\left(2x+3\right)\right]\left[\left(x-2\right)\left(2x+3\right)\right]=0\\ \Leftrightarrow\left(-x-5\right)\left(3x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}-x-5=0\\3x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=\dfrac{-1}{3}\end{matrix}\right.\\ b,\\ \Leftrightarrow\left[3\left(2x+1\right)\right]^2-\left[2\left(x+1\right)\right]^2=0\\ \Leftrightarrow\left[3\left(2x+1\right)-2\left(x+1\right)\right]\left[3\left(2x+1\right)+2\left(x+1\right)\right]=0\\ \Leftrightarrow\left(4x+1\right)\left(8x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}4x+1=0\\8x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-1}{4}\\x=\dfrac{-5}{8}\end{matrix}\right.\\ c,\\ \Leftrightarrow\left[\left(x+1\right)+1\right]^2=0\\ \Leftrightarrow\left(x+1\right)+1=0\\ \Leftrightarrow x+2=0\Rightarrow x=-2\\ d,\\ \Leftrightarrow\left(x-1\right)\left(x-3\right)\left(x+3\right)+\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left[\left(x-1\right)\left(x+3\right)+1\right]=0\\ \Leftrightarrow\left(x+3\right)\left(x^2-4x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+3=0\\\left(x+2\right)^2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-2\end{matrix}\right.\)
\(\left(4B\right)\\ a,\\ \Leftrightarrow49-14x+x^2-4\left(x+25\right)^2=0\\ \Leftrightarrow49-14x+x^2-4x^2-40x-100=0\\ \Leftrightarrow3x^2-54x-51=0\\ \Leftrightarrow-3\left(x^2+18x+17\right)=0\\ \Leftrightarrow\left(x+1\right)\left(x+17\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+1=0\\x+17=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-17\end{matrix}\right.\\ b,\\ \Leftrightarrow4x^2\left(x^2-2x+1\right)-\left(4x^2+4x+1\right)=0\\ \Leftrightarrow x^2-6x=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)
\(c,\\ \Leftrightarrow\left(x+1\right)\left(x^2-x+1\right)=\left(x+1\right)\left(2-x\right)=0\\ \Leftrightarrow\left(x+1\right)\left[\left(x^2-x+1\right)-\left(2-x\right)\right]=0\\ \Leftrightarrow\left(x+1\right)\left(x^1-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+1=0\\x-1=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=1\\x=-1\end{matrix}\right.\\ d,\\ \Leftrightarrow\left(x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-5=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
Phân tích đa thức thành nhân tử (Áp dụng hằng đẳng thức)
10x - 25 - x2
Giúp e vs ạ! E cmơn nhiều !
\(10x-25-x^2=-\left(x^2-10x+25\right)=-\left(x-5\right)^2\)
Chúc bạn học tốt và nhớ click cho mình với nhá!
= (5x-25) + (5x - x2)
= 5(x-5) + x(5-x)
= 5(x-5) - x(x-5)
= (5 - x)(x - 5)
\(10x-25-x^2=-\left(x^2-2\cdot x\cdot5+5^2\right)=-\left(x-5\right)^2\)
Giúp e vs ạ e cảm ơnn nhiều ạ💦
made
felt
began
falled
told
ate
drove
forgot
had