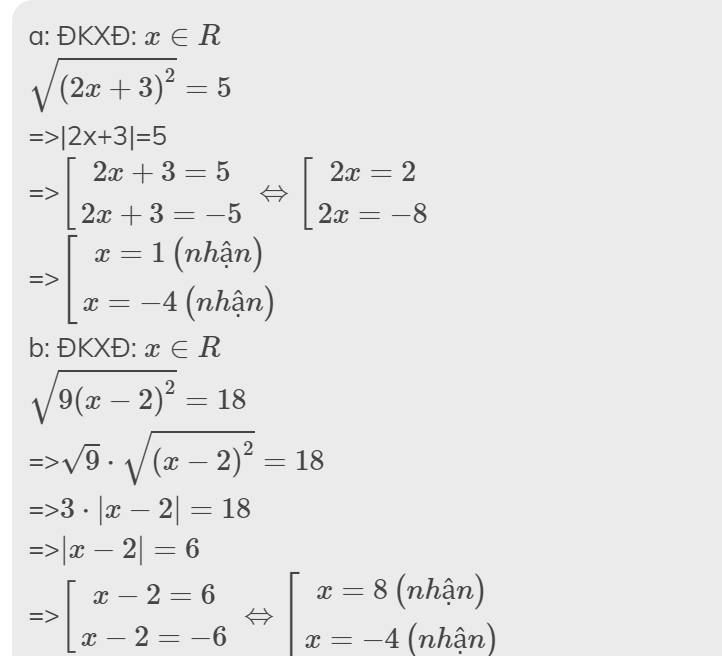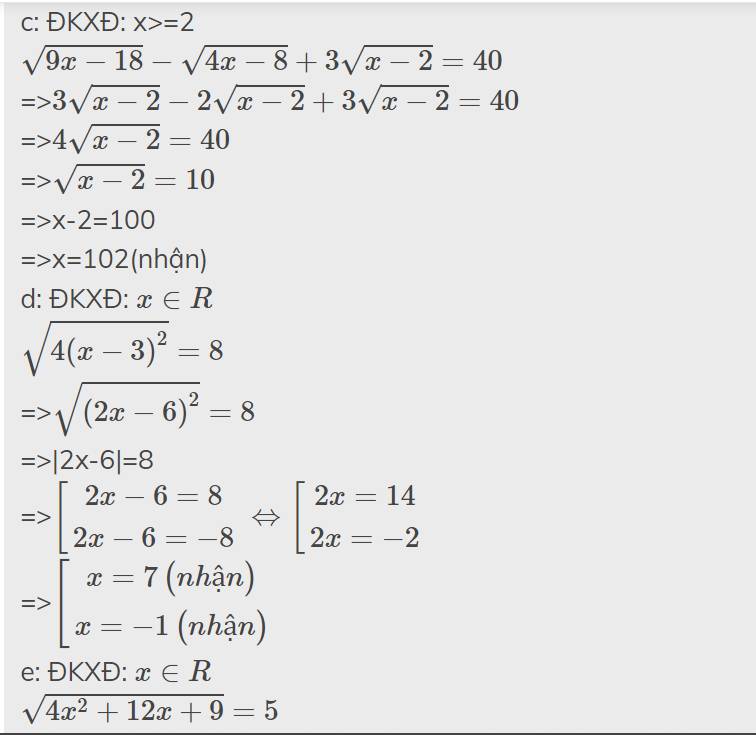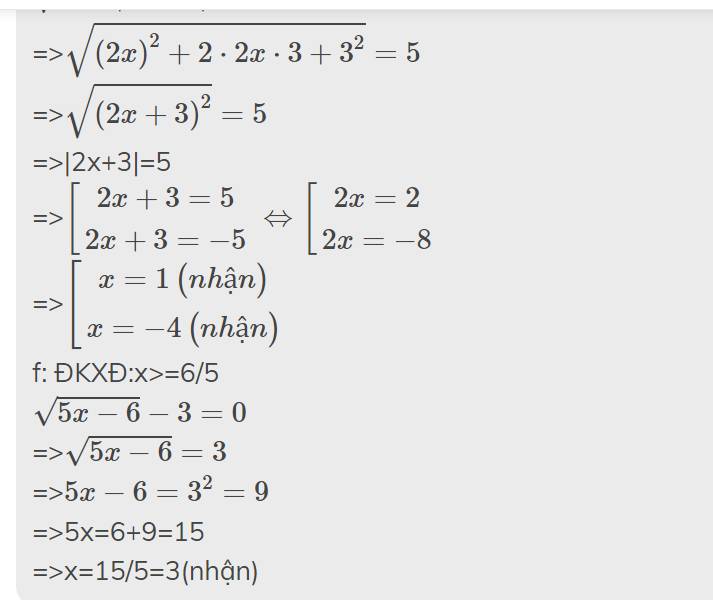ĐKXĐ: x ≥ 2

Phương trình đã cho tương đương:

√(x - 2) + 6√(x - 2) - 2√(x - 2) = 10

⇔ 5√(x - 2) = 10

⇔ √(x - 2) = 2

⇔ x - 2 = 4

⇔ x = 6 (nhận)

Vậy S = {6}

b: ĐKXĐ: x>=2

\(2\sqrt{9x-18}-\sqrt{x-2}+\dfrac{1}{2}\cdot\sqrt{4x-8}=18\)

=>\(2\cdot3\cdot\sqrt{x-2}-\sqrt{x-2}+\dfrac{1}{2}\cdot2\sqrt{x-2}=18\)

=>\(6\sqrt{x-2}=18\)

=>\(\sqrt{x-2}=3\)

=>x-2=9

=>x=11(nhận)

a) Ta có: \(\sqrt{25x+75}+2\sqrt{9x+27}=5\sqrt{x+3}+18\)

\(\Leftrightarrow5\sqrt{x+3}+6\sqrt{x+3}-5\sqrt{x+3}=18\)

\(\Leftrightarrow\sqrt{x+3}=3\)

\(\Leftrightarrow x+3=9\)

hay x=6

b) Ta có: \(\sqrt{4x-8}-14\sqrt{\dfrac{x-2}{49}}=\sqrt{9x-18}+8\)

\(\Leftrightarrow2\sqrt{x-2}-2\sqrt{x-2}-3\sqrt{x-2}=8\)

\(\Leftrightarrow-3\sqrt{x-2}=8\)(Vô lý)

ĐKXĐ: \(x\ge2\)

Ta có: \(\sqrt{4x-8}-\sqrt{9x-18}+2\sqrt{x-2}=1\)

\(\Leftrightarrow2\sqrt{x-2}-3\sqrt{x-2}+2\sqrt{x-2}=1\)

\(\Leftrightarrow\sqrt{x-2}=1\)

\(\Leftrightarrow x-2=1\)

hay x=3(nhận)

Vậy: S={3}

\(3\sqrt{x-2}-\sqrt{4x-8}+4\sqrt{\dfrac{9x-18}{4}}=14\left(x\ge0;x\ne2\right)\\ \Leftrightarrow3\sqrt{x-2}-\sqrt{4\left(x-2\right)}+4\cdot\dfrac{1}{2}\sqrt{9\left(x-2\right)}=14\\ \Leftrightarrow3\sqrt{x-2}-2\sqrt{x-2}+6\sqrt{x-2}=14\\ \Leftrightarrow7\sqrt{x-2}=14\\ \Leftrightarrow\sqrt{x-2}=2\\ \Leftrightarrow x-2=4\\ \Leftrightarrow x=6\left(tm\right)\)

\(a,ĐK:x\ge2\\ PT\Leftrightarrow4\sqrt{x-2}-2\sqrt{x-2}-7\sqrt{x-2}=-10\\ \Leftrightarrow-5\sqrt{x-2}=-10\\ \Leftrightarrow\sqrt{x-2}=2\Leftrightarrow x-2=4\\ \Leftrightarrow x=6\left(tm\right)\\ b,ĐK:x\ge1\\ PT\Leftrightarrow x-3=\sqrt{x-1}\\ \Leftrightarrow x^2-6x+9=x-1\\ \Leftrightarrow x^2-7x+10=0\\ \Leftrightarrow\left(x-2\right)\left(x-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\left(tm\right)\)

a) \(3x-2\sqrt{x-1}=4\) (ĐK: x ≥ 1)

\(\Rightarrow3x-2\sqrt{x-1}-4=0\)

\(\Rightarrow3x-6-2\sqrt{x-1}+2=0\)

\(\Rightarrow3\left(x-2\right)-2\left(\sqrt{x-1}-1\right)=0\)

\(\Rightarrow3\left(x-2\right)-2.\dfrac{x-2}{\sqrt{x-1}+1}=0\)

\(\Rightarrow\left(x-2\right)\left[3-\dfrac{2}{\sqrt{x-1}+1}\right]=0\)

*TH1: x = 2 (t/m)

*TH2: \(3-\dfrac{2}{\sqrt{x-1}+1}=0\)

\(\Rightarrow3=\dfrac{2}{\sqrt{x-1}+1}\)

\(\Rightarrow3\sqrt{x-1}+3=2\)

\(\Rightarrow3\sqrt{x-1}=-1\) (vô lí)

Vậy S = {2}

b) \(\sqrt{4x+1}-\sqrt{x+2}=\sqrt{3-x}\) (ĐK: \(-\dfrac{1}{4}\le x\le3\) )

\(\Rightarrow\sqrt{4x+1}-3-\sqrt{x+2}+2-\sqrt{3-x}+1=0\)

\(\Rightarrow\dfrac{4x-8}{\sqrt{4x+1}+3}-\dfrac{x-2}{\sqrt{x+2}+2}+\dfrac{x-2}{\sqrt{3-x}+1}=0\)

\(\Rightarrow\left(x-2\right)\left(\dfrac{4}{\sqrt{4x+1}+3}-\dfrac{1}{\sqrt{x+2}+2}+\dfrac{1}{\sqrt{3-x}+1}\right)=0\)

=> x = 2

\(a,3x-2\sqrt{x-1}=4\left(x\ge1\right)\\ \Leftrightarrow-2\sqrt{x-1}=4-3x\\ \Leftrightarrow4\left(x-1\right)=16-24x+9x^2\\ \Leftrightarrow9x^2-28x+20=0\\ \Leftrightarrow\left(x-2\right)\left(9x-10\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=\dfrac{10}{9}\left(tm\right)\end{matrix}\right.\)

\(b,\sqrt{4x+1}-\sqrt{x+2}=\sqrt{3-x}\left(-\dfrac{1}{4}\le x\le3\right)\\ \Leftrightarrow4x+1+x+2-2\sqrt{\left(4x+1\right)\left(x+2\right)}=3-x\\ \Leftrightarrow-2\sqrt{\left(4x+1\right)\left(x+2\right)}=2-6x\\ \Leftrightarrow\sqrt{4x^2+9x+2}=3x-1\\ \Leftrightarrow4x^2+9x+2=9x^2-6x+1\\ \Leftrightarrow5x^2-15x-1=0\\ \Leftrightarrow\Delta=225+20=245\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{15-\sqrt{245}}{10}=\dfrac{15-7\sqrt{5}}{10}\left(ktm\right)\\x=\dfrac{15+\sqrt{245}}{10}=\dfrac{15+7\sqrt{5}}{10}\left(tm\right)\end{matrix}\right.\Leftrightarrow x=\dfrac{15+7\sqrt{5}}{10}\)

`a, <=> 5/3 . 3sqrt(x^2+2) + 3/2.2sqrt(x^2+2)-7sqrt6=sqrt(x^2+2)`

`= (5+3-1)sqrt(x^2+2)=7sqrt6`

`<=> 7sqrt(x^2+2)=7sqrt6`.

`<=> x^2+2=36`.

`<=> x^2=34`.

`<=> x=+-sqrt(34)`.

Vậy...

`b, sqrt(4x^2-12x+9)-6=0`

`<=> |2x-3|=6`.

`@ x >=3/2 <=> 2x-3=6.`

`<=> x=9/2 (tm)`.

`@x <3/2 <=> 3-2x=6`

`<=> 2x=-3`

`<=> x=-3/2.`

Vậy...