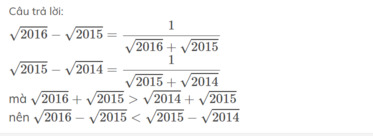so sanh 10\(\sqrt{51}\)va 70+\(\sqrt{2}\)

Những câu hỏi liên quan
So sanh:
a, \(\sqrt{\dfrac{35}{34}}\) va \(\sqrt{\dfrac{71}{70}}\)
b, \(4\sqrt{5}-3\sqrt{2}\) va 5
Khôi Bùi , DƯƠNG PHAN KHÁNH DƯƠNG, Mysterious Person, Phạm Hoàng Giang, Phùng Khánh Linh, Dũng Nguyễn, TRẦN MINH HOÀNG, JakiNatsumi, Hoàng Phong, ...
Đúng 0
Bình luận (0)
Giup minh voi !!! Khôi Bùi,DƯƠNG PHAN KHÁNH DƯƠNG, Phùng Khánh Linh, Nhã Doanh, hattori heiji, Phạm Hoàng Giang, Dũng Nguyễn, ...
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
so sánh 70 + \(\sqrt{2}\)\(\sqrt{2}\)và 10.\(\sqrt{51}\)
so sanh:
a. 2^70 va 3^51
b. 2015/2017 va 2017/2018
351>350=925>825=275>270
Vì 2017<2018 nên\(\frac{1}{2017}\)>\(\frac{1}{2018}\)
⇒\(\frac{2}{2017}\)>\(\frac{1}{2018}\)
⇒\(\frac{2015}{2017}\)=1-\(\frac{2}{2017}\)<1-\(\frac{1}{2018}\)=\(\frac{2017}{2018}\)
Vậy, \(\frac{2015}{2017}\)< \(\frac{2017}{2018}\)
1) So sanh
\(\frac{7}{\sqrt{1}}+\frac{7}{\sqrt{2}}+\frac{7}{\sqrt{3}}+...+\frac{7}{\sqrt{90}}+\frac{7}{\sqrt{100}}.\)va 70
2)Tinh
\(\frac{1}{x^2+3x+2}+\frac{2x}{x^3+4x^2+4x}+\frac{1}{x^2+5x+6}\)
so sanh :\(\sqrt{1999}+\sqrt{2001}..va..2\sqrt{2000}\)
SO SANH
\(-2\sqrt{5}va-5\sqrt{2}\)
\(-2\sqrt{5}=-\sqrt{2^2.5}=-\sqrt{20}\)
\(-5\sqrt{2}=-\sqrt{5^2.2}=-\sqrt{50}\)
\(\Rightarrow-\sqrt{20}>-\sqrt{50}\)
hay \(-2\sqrt{5}>-5\sqrt{2}\)
Đúng 0
Bình luận (0)
\(-2\sqrt{5}=-\sqrt{2^2.5}=-\sqrt{20}\)
\(-5\sqrt{2}=-\sqrt{5^2.2}=-\sqrt{50}\)
vì \(20< 50\)nen \(-\sqrt{20}>-\sqrt{50}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Không tính, so sánh:
\(A=10\sqrt{51}\)và \(B=70+\sqrt{2}\)
đề bài là không dùng máy tính ; hoặc là không khai căn chứ
\(A^2=100.51\)
\(B^2=70^2+2+2.70.\sqrt{2}\)
\(B^2-A^2=70^2-\left(10.7\right)^2+\left(2-2.100\right)+2.70\sqrt{2}\)
\(B^2-A^2=2.70\sqrt{2}-2.99=2\left(70\sqrt{2}-99\right)\)
\(C=70.\sqrt{2};D=99\)
\(C^2=2.70^2\)
\(D^2=99^2=\left(70+29\right)^2\)
\(C^2-D^2=2.70^2-\left(70^2+2.70.29+29^2\right)=70^2-2.70.29-29^2=\left(70-29\right)^2-2.29^2=41^2-2.29^2\)\(C^2-D^2=\left(29+12\right)^2-2.29^2=29^2+12^2+2.29.12=12^2+2.29.12-29^2\)\(C^2-D^2=12^2+2.29.12-12^2-17^2-2.12.17\)\(C^2-D^2=2.12\left(29-17\right)-17^2=2.12^2-17^2\)
\(C^2-D^2=2.12^2-12^2-5^2-2.5.12=12^2-2.5.12-5^2\)
\(C^2-D^2=\left(12-5\right)^2-2.5^2=7^2-2.5^2\)
\(C^2-D^2=5^2+2.2.5+2^2-2.5^2=4.5-5^2+2^2\)
\(C^2-D^2=5\left(4-5\right)+4=4+5.\left(-1\right)=4-5=-1\)
........
=> C^2 -D^2 <0
=>C,D >0
=> C<D => C-D<0
=> B^2 -A^2 <0
A,B >0
=> B<A
kết luận
B<A
Đúng 0
Bình luận (0)
\(A=10\sqrt{51}\); \(B=70+\sqrt{2}\)
Ta có: \(A^2=5100\)
\(B^2=4900+140\sqrt{2}+2\)
So sánh \(198\) và \(140\sqrt{2}\) vì vì trừ 2 vế cho 4902.
Ta có: \(198^2=39204\)
\(\left(140\sqrt{2}\right)^2=39200\)
Vậy A > B (đpcm)
Đúng 0
Bình luận (1)
ta có :
\(A^2=\left(10\sqrt{51}\right)^2=100\cdot51=5100\)
\(B^2=\left(70+\sqrt{2}\right)^2=4900+140\sqrt{2}+2=4902+140\sqrt{2}\)
Cùng trừ 2 vế cho 4902 ta dc:
\(A^2=5100-4902=198\)
\(B^2=4902+140\sqrt{2}-4902=140\sqrt{2}\)
ta có :
A= \(198^2=39204\)
B= \(\left(140\sqrt{2}\right)^2=39200\)
vì 39204>39200 nên 10\(\sqrt{51}\)>70+\(\sqrt{2}\)
vậy A>B
Đúng 0
Bình luận (0)
So sanh : \(\sqrt{2016}-\sqrt{2015}va\sqrt{\sqrt{2015}-}\sqrt{2014}\)
So sanh: x=\(\sqrt{2019}\) va y=\(2\sqrt{2018}-\sqrt{2017}\)