Viết phương trình chính tắc của elip trong hình 4.
Những câu hỏi liên quan
Viết phương trình chính tắc của elip đi qua điểm A(0;-4) và có 1 tiêu điểm F2(3;0)
Gọi ptr chính tắc của `(E)` có dạng: `[x^2]/[a^2]+[y^2]/[b^2]=1`
Thay `A(0;-4)` vào `(E)` có:
`16/[b^2]=1<=>b^2=16`
Vì `F_2 (3;0)=>c=3=>c^2=9`
Ta có: `a^2=b^2+c^2`
`<=>a^2=16+9`
`<=>a^2=25`
Vậy ptr chính tắc của `(E)` là: `[x^2]/25+[y^2]/16=1`
Đúng 2
Bình luận (0)
Viết phương trình chính tắc của elip đi qua điểm A(0;-4) và có 1 tiêu điểm F2(3;0)
viết phương trình chính tắc của elip đi qua điểm A(0;-4) và có 1 tiêu điểm F2(3;0)
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)(E)
Thay x=0 và y=-4 vào (E), ta được:
16/b^2=1
=>b=4
F2(3;0)
=>c=3
=>căn a^2-16=3
=>a^2-16=9
=>a=5
=>x^2/25+y^2/16=1
Đúng 1
Bình luận (0)
Trong mặt phẳng Oxy , viết phương trình chính tắc của Elip có một tiêu điểm là F1(-2;0) và đi qua điểm M(2;3)
F1(-2;0) nên c=-2
=>c^2=4
=>c^2=a^2-b^2=4
=>a^2=b^2+4
(E): x^2/a^2+y^2/b^2=1
Thay x=2 và y=3 vào (E), ta được:
2^2/a^2+3^2/b^2=1
=>4/a^2+9/b^2=1
=>\(\dfrac{4}{b^2+4}+\dfrac{9}{b^2}=1\)
=>\(\dfrac{13b^2+36}{b^2\left(b^2+4\right)}=1\)
=>b^4+4b^2-13b^2-36=0
=>b^2=12
=>b=2căn 3
=>a=4
=>(E): x^2/16+y^2/12=1
Đúng 1
Bình luận (1)
Trong mặt phẳng Oxy, phương trình nào sau đây là phương trình chính tắc của một elip? A.
x
2
2
+
y
2
3
1
B.
x
2
9
-
y
2
8...
Đọc tiếp
Trong mặt phẳng Oxy, phương trình nào sau đây là phương trình chính tắc của một elip?
A. x 2 2 + y 2 3 = 1
B. x 2 9 - y 2 8 = 1
C. x 9 + y 8 = 1
D. x 2 9 + y 2 1 = 1
Viết phương trình chính tắc của elip,tiêu cự bằng 8 độ dài trục lớn bằng 10
Viết phương trình chính tắc của elip biết tiêu điểm F1 = (-√3;0) và đi qua M (√3 ; ½)?
F1(\(-\sqrt{3};0\)) => c=\(\sqrt{3}\)
có: \(b^2=a^2-c^2=a^2-3\)
pt elip di qua M:
\(\dfrac{3}{a^2}+\dfrac{1}{4b^2}=1\)
\(\Leftrightarrow\dfrac{3}{a^2}+\dfrac{1}{4a^2-12}=1\)
dat a^2=t (t>0)
\(\Leftrightarrow\dfrac{3}{t}+\dfrac{1}{4t-12}=1\\ \Leftrightarrow12t-36+t=4t^2-12t\)
\(\Leftrightarrow4t^2-25t+36=0\\ \Leftrightarrow\left[{}\begin{matrix}t=4\\t=\dfrac{9}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a^2=4\\a^2=\dfrac{9}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}b^2=1\\b^2=-\dfrac{3}{4}\left(loai\right)\end{matrix}\right.\)
=>ptelip: \(\dfrac{x^2}{4}+\dfrac{y^2}{1}=1\)
Đúng 1
Bình luận (0)
Lập phương trình chính tắc của elip trong trường hợp sau: Elip có một tiêu điểm là
F
1
-
3
;
0
và điểm
M
1
;
3
2
nằm trên elip...
Đọc tiếp
Lập phương trình chính tắc của elip trong trường hợp sau: Elip có một tiêu điểm là F 1 - 3 ; 0 và điểm M 1 ; 3 2 nằm trên elip.
Gọi Elip cần tìm có dạng : (E) :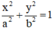 
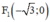là tiêu điểm của (E) ⇒ a2 – b2 = 3 ⇒ a2 = b2 + 3
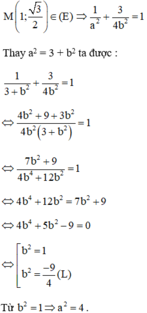
Phương trình chính tắc của Elip là :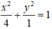 
Đúng 1
Bình luận (0)
Phương trình
x
2
m
2
+
y
2
36
1
là phương trình chính tắc của elip có hình chữ nhật cơ sở với diện tích bằng 300 thì: A.
m
±
5
2
B.
m
±
15
2...
Đọc tiếp
Phương trình x 2 m 2 + y 2 36 = 1 là phương trình chính tắc của elip có hình chữ nhật cơ sở với diện tích bằng 300 thì:
A. m = ± 5 2
B. m = ± 15 2
C. m = ± 25 2
D. Không tồn tại m
