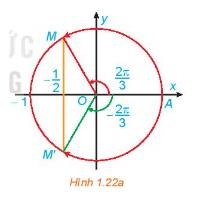
a) Quan sát Hình 1.22a, tìm các nghiệm của phương trình đã cho trong nửa khoảng \(\left[ { - \pi ;\pi } \right)\).
b) Dựa vào tính tuần hoản của hàm số cosin, hãy viết công thức nghiệm của phương trình đã cho.
a) Quan sát Hình 1.19, tìm các nghiệm của phương trình đã cho trong nửa khoảng \(\left[ {0;2\pi } \right)\)
b) Dựa vào tính tuần hoàn của hàm số sin, hãy viết công thức nghiệm của phương trình đã cho
a) Từ Hình 1.19, ta thấy đường thẳng \(y = \frac{1}{2}\) cắt đường tròn tại 2 điểm M, M’. Ta có nghiệm của phương trình là: \(\frac{\pi }{6}, - \frac{{5\pi }}{6}\)
b) Vì hàm số \(\sin x\) tuần hoàn với chu kỳ là \(2\pi \), ta có công thức nghiệm của phương trình là: \(\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{6} + k2\pi }\\{x = \pi - \frac{\pi }{6} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\)
a) Quan sát Hình 1.25, hãy cho biết đường thẳng \(y = - 1\) cắt đồ thị hàm số \(y = \cot x\) tại mấy điểm trên khoảng \(\left( {0;\pi } \right)?\)

b) Dựa vào tính tuần hoàn của hàm cotang, hãy viết công thức nghiệm của phương trình đã cho.
a) Từ Hình 1.25, ta thấy đường thẳng \(y = - 1\) cắt đồ thị hàm số \(y = \cot x\;\)tại 1 điểm \(x = - \frac{\pi }{4} + \pi \) trên khoảng \(\left( {0;\pi } \right)\)
b) Ta có công thức nghiệm của phương trình là: \(x = - \frac{\pi }{4} + \pi + k\pi \;\left( {k \in \mathbb{Z}} \right)\)
a) Quan sát Hình 1.24, hãy cho biết đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = \tan x\) tại mấy điểm trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)?\)
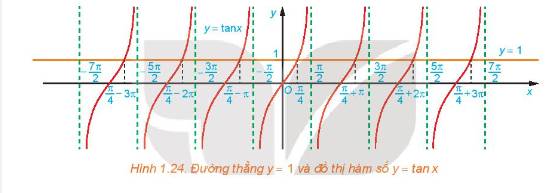
b) Dựa vào tính tuần hoàn của hàm tang, hãy viết công thức nghiệm của phương trình đã cho
a) Từ Hình 1.24, ta thấy đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = \tan x\;\)tại 1 điểm \(x = \frac{\pi }{4}\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\)
b) Ta có công thức nghiệm của phương trình là: \(x = \frac{\pi }{4} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)
tìm nghiệm của các phương trình sau trong khoảng đã cho : a) \(\sin2x=-\frac{1}{2}\) với \(0\le x\le\pi\) ; b) \(\cos\left(x-5\right)\) với \(-\pi\le x\le\pi\)
tìm nghiệm của các phương trình sau trong khoảng đã cho : a) \(\sin2x=-\frac{1}{2}\) với \(0\le x\le\pi\) ; b) \(\cos\left(x-5\right)=\frac{\sqrt{3}}{2}\) với \(-\pi\le x\le\pi\)
tìm nghiệm của các phương trình sau trong khoảng đã cho : a) \(\sin2x=-\frac{1}{2}\) với \(0\le x\le\pi\) ; b) \(\cos\left(x-5\right)=\frac{\sqrt{3}}{2}\) với \(-\pi\le x\le\pi\)
tìm nghiệm của các phương trình sau trong khoảng đã cho :
a) \(\sin2x=-\frac{1}{2}\) với \(0\le x\le\pi\)
b) \(\cos\left(x-5\right)=\frac{\sqrt{3}}{2}\) với \(-\pi\le x\le\pi\)
Cho phương trình (1-Sinx)(Cos2x + 3mSinx+Sinx-1)=\(mCos^2x\) (m là tham số). Tìm các giá trị thực của m để phương trình có 6 nghiệm khác nhau thuộc khoảng \(\left(-\dfrac{\Pi}{2};2\Pi\right)\)
\(\Leftrightarrow\left(1-sinx\right)\left(cos2x+3msinx+sinx-1\right)=m\left(1-sinx\right)\left(1+cosx\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=1\Rightarrow x=\dfrac{\pi}{2}\\cos2x+3m.sinx+sinx-1=m\left(1+sinx\right)\left(1\right)\end{matrix}\right.\)
Bài toán thỏa mãn khi (1) có 5 nghiệm khác nhau trên khoảng đã cho thỏa mãn \(sinx\ne1\)
Xét (1):
\(\Leftrightarrow1-2sin^2x+3msinx+sinx-1=m+m.sinx\)
\(\Leftrightarrow2sin^2x-sinx-2m.sinx+m=0\)
\(\Leftrightarrow sinx\left(2sinx-1\right)-m\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx-m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\Rightarrow x=\dfrac{\pi}{6};\dfrac{5\pi}{6}\\sinx=m\left(2\right)\end{matrix}\right.\)
\(\Rightarrow\left(2\right)\) có 3 nghiệm khác nhau trên \(\left(-\dfrac{\pi}{2};2\pi\right)\)
\(\Leftrightarrow-1< m< 0\)
Câu 1: Tích các nghiệm trên khoảng \(\left(\dfrac{\pi}{4};\dfrac{7\pi}{4}\right)\)của phương trình \(cos2x-3cosx+2=0\)
Câu 2: Tìm tất cả các giá trị thực của tham số m để phương trình \(2cos^23x+\left(3-2m\right)cos3x+m-2=0\) có đúng 3 nghiệm thuộc khoảng \(\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\).
Câu 3: Tính tổng T tất cả các nghiệm của phương trình \(2sin^2\dfrac{x}{4}-3cos\dfrac{x}{4}=0\) trên đoạn \(\left[0;8\pi\right]\).
Câu 4: Giá trị của m để phương trình \(cos2x-\left(2m+1\right)sinx-m-1=0\) có nghiệm trên khoảng \(\left(0;\pi\right)\) là \(m\in[a;b)\) thì a+b là?
Câu 5: Điều kiện cần và đủ để phương trình \(msinx-3cosx=5\) có nghiệm là \(m\in(-\infty;a]\cup[b;+\infty)\) với \(a,b\in Z\). Tính a+b.
Câu 6: Điều kiện để phương trình \(msinx-3cosx=5\) có nghiệm là?
Câu 7: Số nghiệm để phương trình \(sin2x+\sqrt{3}cos2x=\sqrt{3}\) trên khoảng \(\left(0;\dfrac{\pi}{2}\right)\) là?
Câu 8: Tập giá trị của hàm số \(y=\dfrac{sinx+2cosx+1}{sinx+cosx+2}\) là?
Câu 9: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn \(\left[-2018;2018\right]\) dể phương trình \(\left(m+1\right)sin^2-sin2x+cos2x=0\) có nghiệm?
Câu 10: Có bao nhiêu giá trị nguyên của tham số m để phương trình \(sin2x-cos2x+|sinx+cosx|-\sqrt{2cos^2x+m}-m=0\) có nghiệm thực?
1.
\(cos2x-3cosx+2=0\)
\(\Leftrightarrow2cos^2x-3cosx+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pm\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(x=k2\pi\in\left[\dfrac{\pi}{4};\dfrac{7\pi}{4}\right]\Rightarrow\) không có nghiệm x thuộc đoạn
\(x=\pm\dfrac{\pi}{3}+k2\pi\in\left[\dfrac{\pi}{4};\dfrac{7\pi}{4}\right]\Rightarrow x_1=\dfrac{\pi}{3};x_2=\dfrac{5\pi}{3}\)
\(\Rightarrow P=x_1.x_2=\dfrac{5\pi^2}{9}\)
2.
\(pt\Leftrightarrow\left(cos3x-m+2\right)\left(2cos3x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos3x=\dfrac{1}{2}\left(1\right)\\cos3x=m-2\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow x=\pm\dfrac{\pi}{9}+\dfrac{k2\pi}{3}\)
Ta có: \(x=\pm\dfrac{\pi}{9}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=\pm\dfrac{\pi}{9}\)
Yêu cầu bài toán thỏa mãn khi \(\left(2\right)\) có nghiệm duy nhất thuộc \(\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}m-2=0\\m-2=1\\m-2=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=2\\m=3\\m=1\end{matrix}\right.\)
TH1: \(m=2\)
\(\left(2\right)\Leftrightarrow cos3x=0\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=\dfrac{\pi}{6}\left(tm\right)\)
\(\Rightarrow m=2\) thỏa mãn yêu cầu bài toán
TH2: \(m=3\)
\(\left(2\right)\Leftrightarrow cos3x=0\Leftrightarrow x=\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=0\left(tm\right)\)
\(\Rightarrow m=3\) thỏa mãn yêu cầu bài toán
TH3: \(m=1\)
\(\left(2\right)\Leftrightarrow cos3x=-1\Leftrightarrow x=\dfrac{\pi}{3}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow\left[{}\begin{matrix}x=\pm\dfrac{1}{3}\\x=-1\\x=-\dfrac{5}{3}\end{matrix}\right.\)
\(\Rightarrow m=2\) không thỏa mãn yêu cầu bài toán
Vậy \(m=2;m=3\)
3.
\(2sin^2\dfrac{x}{4}-3cos\dfrac{x}{4}=0\)
\(\Leftrightarrow2cos^2\dfrac{x}{4}+3cos\dfrac{x}{4}-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos\dfrac{x}{4}=\dfrac{1}{2}\\cos\dfrac{x}{4}=-2\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow x=\pm\dfrac{4\pi}{3}+k8\pi\in\left[0;8\pi\right]\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4\pi}{3}\\x=\dfrac{20\pi}{3}\end{matrix}\right.\)
\(\Rightarrow T=\dfrac{4\pi}{3}+\dfrac{20\pi}{3}=8\pi\)