Câu 25 ạ 

Những câu hỏi liên quan
Câu 25-30 ạ
Giúp e giải câu 24 25 với ạ e cần gấp ạ
Giúp em câu 25 ạ. 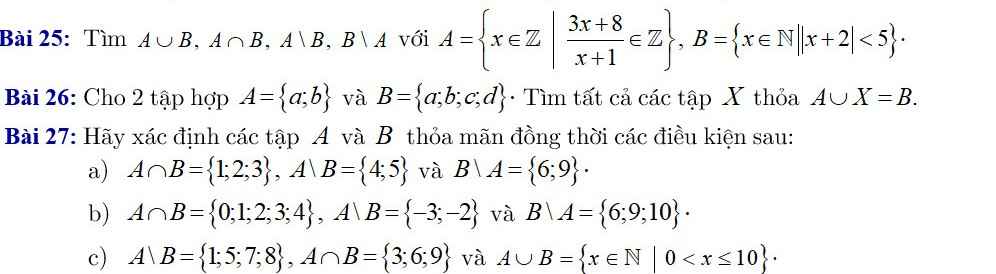
Giup mik câu 25 ạ 
Ukm, mình nghĩ là bạn chọn đúng rồi đó,vì đáp án A,C và D không có liên quan gì đến việc tuyên truyền phòng tránh.Tích cực tham gia tuyên truyền phòng chống ma túy thông qua các hoạt động ngoại khóa là trách nhiệm của học sinh trong việc thực hiện vấn đề cấp thiết Bảo vệ môi trường sống của nhân loại.
Mình giúp luôn phần tự luận nhe :)
\(II.Tự.luận\)
Câu 1 :
Nhận xét về quan điểm trên : Em không đồng tình với quan điểm trên bởi nếu như không đăng kí kết hôn mà đã sống chung như vợ chồng thì pháp luật hay nhà nước sẽ không chấp nhận cuộc hôn nhân này, Nếu muốn được pháp luật , nhà nước công nhận thì phải đăng kí kết hôn.
Câu 2 :
Hiện nay, dịch bệnh hiểm nghèo đang uy hiếp đến sự sống của toàn nhân loại. Là học sinh, em cần làm một số việc sau để góp phần tham gia phòng ngừa và đẩy lùi dịch bệnh hiểm nghèo :
- Tuyên truyền và vận động người thân, bạn bè và một số người xung quanh nơi em sống.
- Bình tĩnh và tìm ra cách xử lí để phòng ngừa dịch bệnh.
- Nhờ sự giúp đỡ từ những nhà bác sĩ nổi tiếng để cùng nhau tìm ra và sáng chế ra loại thuốc để phòng dịch bệnh hiểm nghèo này.
- Làm thông điệp để cùng mọi người xung quanh thực hiện, như vậy mới đẩy lùi được dịch bệnh hiểm nghèo này.
Đúng 2
Bình luận (0)
Giúp mình câu 10-25 với ạ(chuyển các câu sau thành câu bị động)
10. a present was sent to me last week
11. More information was given to us by her
Đúng 0
Bình luận (0)
Cho mình hỏi câu 24 câu 25 đáp án là gì ạ?

Câu 23, 24 và 25 ạ
Giải chi tiết ra giúp em với ạ

23.
Ta sẽ tìm điểm \(I\left(a;b;c\right)\) sao cho \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\) (1)
\(\left\{{}\begin{matrix}\overrightarrow{IA}=\left(-2-a;2-b;6-c\right)\\\overrightarrow{IB}=\left(-3-a;1-b;8-c\right)\\\overrightarrow{IC}=\left(-1-a;-b;7-c\right)\\\overrightarrow{ID}=\left(1-a;2-b;3-c\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\left(-5-4a;5-4b;24-4c\right)\)
(1) thỏa mãn khi: \(\left\{{}\begin{matrix}-5-4a=0\\5-4b=0\\24-4c=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{4}\\b=\dfrac{5}{4}\\c=6\end{matrix}\right.\)
\(\Rightarrow I\left(-\dfrac{5}{4};\dfrac{5}{4};6\right)\)
Khi đó:
\(T=MA^2+MB^2+MC^2+MD^2=\left(\overrightarrow{MI}+\overrightarrow{IA}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IB}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IC}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{ID}\right)^2\)
\(=4MI^2+IA^2+IB^2+IC^2+ID^2+2\overrightarrow{MI}\left(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}\right)\)
\(=4MI^2+IA^2+IB^2+IC^2+ID^2\) (do \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\))
\(IA^2+IB^2+IC^2+ID^2\) cố định nên \(T_{min}\) khi \(MI_{min}\)
\(\Leftrightarrow M\) trùng I
\(\Rightarrow M\left(-\dfrac{5}{4};\dfrac{5}{4};6\right)\Rightarrow x+y+z=-\dfrac{5}{4}+\dfrac{5}{4}+6=6\)
Đúng 1
Bình luận (0)
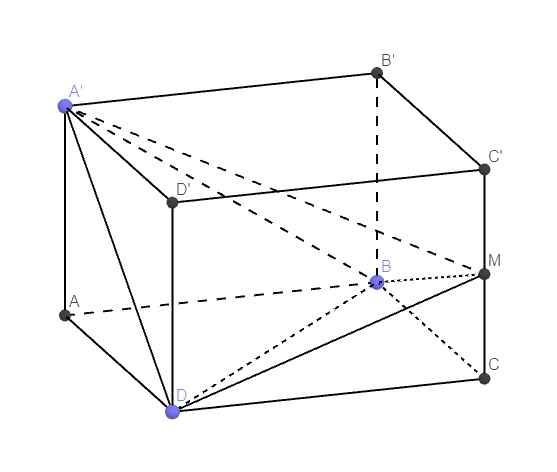
24.
\(a+b=4\Rightarrow b=4-a\)
ABCD là hình chữ nhật \(\Rightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow C\left(a;a;0\right)\)
Tương tự ta có: \(C'\left(a;a;b\right)\)
M là trung điểm CC' \(\Rightarrow M\left(a;a;\dfrac{b}{2}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{A'B}=\left(a;0;-b\right)=\left(a;0;a-4\right)\\\overrightarrow{A'D}=\left(0;a;-b\right)=\left(0;a;a-4\right)\\\overrightarrow{A'M}=\left(a;a;-\dfrac{b}{2}\right)=\left(a;a;\dfrac{a-4}{2}\right)\end{matrix}\right.\)
Theo công thức tích có hướng:
\(\left[\overrightarrow{A'B};\overrightarrow{A'D}\right]=\left(-a^2+4a;-a^2+4a;a^2\right)\)
\(\Rightarrow V=\dfrac{1}{6}\left|\left[\overrightarrow{A'B};\overrightarrow{A'D}\right].\overrightarrow{A'M}\right|=\dfrac{1}{6}\left|a\left(-a^2+4a\right)+a\left(-a^2+4a\right)+\dfrac{a^2\left(a-4\right)}{2}\right|\)
\(=\dfrac{1}{4}\left|a^3-4a^2\right|=\dfrac{1}{4}\left(4a^2-a^3\right)\)
Xét hàm \(f\left(a\right)=\dfrac{1}{4}\left(4a^2-a^3\right)\) trên \(\left(0;4\right)\)
\(f'\left(a\right)=\dfrac{1}{4}\left(8a-3a^2\right)=0\Rightarrow\left[{}\begin{matrix}a=0\left(loại\right)\\a=\dfrac{8}{3}\end{matrix}\right.\)
\(\Rightarrow f\left(a\right)_{max}=f\left(\dfrac{8}{3}\right)=\dfrac{64}{27}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giúp mình với ạ mình đang cần gấp ! Từ câu 10 tới 25 ạ !
10 C
11 A
12 D
13 B
14 D
15 D
16 B
17 A
18 C
19 D
20 B
21 B
22 C
23 A
24 A
25 C
Đúng 1
Bình luận (0)

Giúp mình câu 25 với ạ