Bạn hãy tìm hiểu về Ma-la-la Diu-sa-phdai, Ngày Ma-la-la và chia sẻ với các thành viên trong lớp.

Những câu hỏi liên quan
Tìm hiểu một nét văn hoá Mỹ La-tinh và chia sẻ với các bạn.
Mình lấy VD các bạn tự tìm hiểu sâu nhé!
- Lễ hội Đốt cháy tâm trạng tồi tệ (Mexico)
- Lễ hội Truyền thống bùn (Brazil)
- Lễ Kỷ niệm tuyết (Paraguay)
- v.v.v....
Đúng 0
Bình luận (0)
Ví dụ: Lễ hội Ca-na-van
- Lễ hội được tổ chức từ 28/2 - 4/3 hàng năm trên khắp đất nước Bra-xin, trong đó tại thủ đô Ri-ô Gia-nây-rô là nơi hội tụ tất cả các vũ công Samba tài giỏi nhất đổ về tranh tài.
- Nhắc tới lễ hội Ca-na-van là nhắc đến những bộ trang phục hóa trang lộng lẫy của các vũ công Samba, tại đây bạn có thể tận mắt chiêm ngưỡng nhiều bộ trang phục mà chưa bao giờ được thấy trong đời.
- Lễ hội là sự gắn liền với các buổi lễ diễu hành cạnh tranh giữa các trường học dạy Samba. Mỗi trường lại có vũ công, biên đạo múa và nhạc sĩ của riêng mình, tạo nên các màn trình diễn độc đáo.
Đúng 0
Bình luận (0)
Giả sử chúng ta muốn tới thăm thủ đô của nước trong khu vực Đông Nam Á bằng máy bay. Dựa vào bản đồ hình 12, hãy cho biết các hướng bay từ: - Hà Nội đến Viêng Chăn. - Cu-a-la Lăm-pơ đến Băng Cốc. - Hà Nội đến Gia-các-ta. - Cu-a-la Lăm-pơ đến Ma-ni-la. - Hà Nội đến Ma-ni-la. - Ma-ni-la đến Băng Cốc.
Đọc tiếp
Giả sử chúng ta muốn tới thăm thủ đô của nước trong khu vực Đông Nam Á bằng máy bay. Dựa vào bản đồ hình 12, hãy cho biết các hướng bay từ:
- Hà Nội đến Viêng Chăn.
- Cu-a-la Lăm-pơ đến Băng Cốc.
- Hà Nội đến Gia-các-ta.
- Cu-a-la Lăm-pơ đến Ma-ni-la.
- Hà Nội đến Ma-ni-la.
- Ma-ni-la đến Băng Cốc.
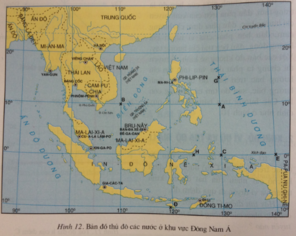
- Hướng bay từ Hà Nội đến Viêng Chăn là hướng tây nam.
- Hướng bay từ Cu-a-la Lăm-pơ đến Băng Cốc là hướng bắc.
- Hướng bay từ Hà Nội đến Gia-các-ta là hướng nam.
- Hướng bay từ Cu-a-la Lăm-pơ đến Ma-ni-la là hướng đông bắc.
- Hướng bay từ Hà Nội đến Ma-ni-la là hướng đông nam.
- Hướng bay từ Ma-ni-la đến Băng Cốc là hướng tây.
Đúng 0
Bình luận (0)
Trình bày về một nét văn hoá Mỹ La Tinh và chia sẻ với các bạn của em ( Bức Thư) không chép mạng xin cảm ơn.
Câu 8: các đồn bằng lớn hơn của Nam Mĩ xếp theo thứ tụ nào từ Bắc xuống Nam là đúng ?
A .a-ma-dôn , pam-pa , la-pla-ta
B . pam-pa , a-ma-dôn, la-pla-ta
C . pam-pa , la-pla-ta, a-ma-dôn
D . a-ma-dôn , la-pla-ta , pam-pa
Cho tam giác ABC có độ dài phân giác trong là la, lb, lc. CMR: la ≤ ma và la+lb+lc≤p√3
Không mất tính tồng quát, giả sử \(AB\le AC\)
Gọi M và D lần lượt là trung điểm và chân đường phân giác trong góc A trên BC
Theo định lý phân giác: \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\Rightarrow\dfrac{CD}{AC}=\dfrac{BD}{AB}\ge\dfrac{BD}{AC}\Rightarrow CD\ge BD\)
\(\Rightarrow BD\le BC-BD\Rightarrow BD\le\dfrac{1}{2}BC\)
\(\Rightarrow BD\le BM\)
\(\Rightarrow AD\le AM\) hay \(l_a\le m_a\)(đpcm)
Đặt \(A=l_a+l_b+l_c=\dfrac{2bc}{b+c}cos\dfrac{A}{2}+\dfrac{2ca}{c+a}cos\dfrac{B}{2}+\dfrac{2ab}{a+b}cos\dfrac{C}{2}\)
\(\Rightarrow A^2=\left(\dfrac{2bc}{b+c}cos\dfrac{A}{2}+\dfrac{2ca}{c+a}cos\dfrac{B}{2}+\dfrac{2ab}{a+b}cos\dfrac{C}{2}\right)^2\)
\(\Rightarrow A^2\le\left[\dfrac{4b^2c^2}{\left(b+c\right)^2}+\dfrac{4c^2a^2}{\left(c+a\right)^2}+\dfrac{4a^2b^2}{\left(a+b\right)^2}\right]\left(cos^2\dfrac{A}{2}+cos^2\dfrac{B}{2}+cos^2\dfrac{C}{2}\right)\)
Áp dụng BĐT cơ bản \(\left(x+y\right)\ge4xy\) ta có:
\(\dfrac{4b^2c^2}{\left(b+c\right)^2}+\dfrac{4c^2a^2}{\left(c+a\right)^2}+\dfrac{4a^2b^2}{\left(a+b\right)^2}\le\dfrac{4b^2c^2}{4bc}+\dfrac{4c^2a^2}{4ca}+\dfrac{4a^2b^2}{4ab}\)
\(=ab+bc+ca\le\dfrac{1}{3}\left(a+b+c\right)^2\)
Đồng thời:
\(cos^2\dfrac{A}{2}+cos^2\dfrac{B}{2}+cos^2\dfrac{C}{2}=\dfrac{3+cosA+cosB+cosC}{2}\le\dfrac{3+\dfrac{3}{2}}{2}=\dfrac{9}{4}\)
\(\Rightarrow A^2\le\dfrac{9}{4}.\dfrac{1}{3}\left(a+b+c\right)^2\)
\(\Rightarrow A\le\sqrt{3}\left(\dfrac{a+b+c}{2}\right)=p\sqrt{3}\) (đpcm)
Dấu "=" xảy ra khi tam giác ABC đều
Đúng 0
Bình luận (1)
Cho goc xOz = 120 do, Oy la tia phan giac cua goc xOz, Ot la tia phan giac cua goc yOz. M la mot diem thuoc mien trong cua goc yOz. Ve MA vuong goc voi Ox, vẽ MB vuông góc với Oy, vẽ Mc vuông góc với Ot. Tính OC theo MA và MB.
CM la so may trong so la ma
M trong so la ma la so nao
so 46 ghi trong he la ma la























