e: =>x(x^3-4x^2-8x+8)=0

=>x[(x^3+8)-4x(x+2)]=0

=>x(x+2)(x^2-2x+4-4x)=0

=>x(x+2)(x^2-6x+4)=0

=>\(x\in\left\{0;-2;3+\sqrt{5};3-\sqrt{5}\right\}\)

g: =>2x^4+5x^3-6x^3-15x^2+6x^2+15x-2x-5=0

=>(2x+5)(x^3-3x^2+3x-1)=0

=>(2x+5)(x-1)^3=0

=>x=1 hoặc x=-5/2

h: =>(x^2+8x+7)(x^2+8x+15)+15=0

=>(x^2+8x)^2+22(x^2+8x)+120=0

=>(x^2+8x+10)(x^2+8x+12)=0

=>(x^2+8x+10)(x+2)(x+6)=0

=>\(x\in\left\{-2;-6;-4+\sqrt{6};-4-\sqrt{6}\right\}\)

`Q(-2)=(-2)^4+4*(-2)^3+2*(-2)^2-4*(-2)+1`

`= 16+4*(-8)+2*4+8+1`

`= 16-32+8+8+1`

`= -16+8+8+1`

`= -8+8+1=1`

`Q(1)=1^4+4*1^3+2*1^2-4*1+1`

`= 1+4+2-4+1`

`= 2+2+4-4=4`

Q(-2) = (-2)⁴ + 4.(-2)³ + 2.(-2)² - 4.(-2) + 1

= 16 - 32 + 8 + 8 + 1

= 1

--------------------

Q(1) = 1⁴ + 4.1³ + 2.1² - 4.1 + 1

= 1 + 4 + 2 - 4 + 1

= 4

Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:

* Ta có: f(x) = x7 – 3x2 – x5 + x4 – x2 + 2x – 7

            = x7 - (3x2+ x2) – x5+ x4 + 2x – 7

            = x7 – 4x2 – x5+ x4 + 2x – 7

            = x7 – x5 + x4 – 4x2 + 2x - 7

g(x) = x – 2x2 + x4 – x5 – x7 – 4x2 – 1

            = x – ( 2x2 + 4x2) + x4 – x5 –x7 – 1

            = x – 6x2 + x4 – x5 – x7 – 1

            = -x7 – x5 + x4 – 6x2 + x – 1

* f(x) – g(x)

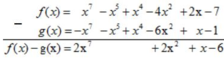
Vậy f(x) – g(x) = 2x7 + 2x2 + x - 6

f(x) = x5 + 3x2 − 5x3 − x7 + x3 + 2x2 + x5 − 4x2 + x7

= (x5 + x5) + (3x2 + 2x2 – 4x2) + (-5x3 + x3) + (-x7 + x7)

= 2x5 + x2 – 4x3.

= 2x5 - 4x3 + x2

Đa thức có bậc là 5

g(x) = x4 + 4x3 – 5x8 – x7 + x3 + x2 – 2x7 + x4 – 4x2 – x8

= (x4 + x4) + (4x3 + x3) – (5x8 + x8) – (x7 + 2x7) + (x2 – 4x2)

= 2x4 + 5x3 – 6x8 – 3x7 – 3x2

= -6x8 - 3x7 + 2x4 + 5x3 - 3x2.

Đa thức có bậc là 8.

Đa thức có bậc là 5 nhe

\(a,A\left(x\right)=-3x^3+2x^2-6+5x+4x^3-2x^2-4-4x\\ =\left(-3x^3+4x^3\right)+\left(2x^2-2x^2\right)+\left(5x-4x\right)+\left(-6-4\right)\\ =x^3+0+x-10\\ =x^3+x-10\)

Bậc của đa thức \(3\)

Hệ số cao nhất là \(1\)

\(b,B\left(x\right)=A\left(x\right).\left(x-1\right)=\left(x^3+x-10\right)\left(x-1\right)\\ =x^3.x+x.x-10x-x^3-x+10\\ =x^4+x^2-x^3-x-10x+10\\ =x^4-x^3+x^2-11x+10\)

Thay \(x=2\) vào \(B\left(x\right)\)

\(=2^4-2^3+2^2-11.2+10\\ =0\) 

Vậy tại \(x=2\) thì \(B\left(x\right)=0\)

\(Q\left(x\right)=x^4+4x^3+2x^2-4x+1\)

\(\Rightarrow Q\left(-2\right)=\left(-2\right)^4+4\cdot\left(-2\right)^3+2\cdot\left(-2\right)^2-4\cdot\left(-2\right)+1=1\)

\(Q\left(-1\right)=\left(-1\right)^4+4\cdot\left(-1\right)^3+2\cdot\left(-1\right)^2-4\cdot\left(-1\right)+1=4\)

\(P\left(-1\right)=\left(-1\right)^4+2.\left(-1\right)^2+1=4\\ P\left(1\right)=1^4+2.1^2+1=4\)

\(P\left(-1\right)=\left(-1\right)^4+2\cdot\left(-1\right)^2+1=4\)

\(P\left(1\right)=P\left(-1\right)=4\)

\(Q\left(2\right)=2^4+4\cdot2^3+2\cdot2^2-4\cdot2+1=49\)

\(Q\left(1\right)=1^4+4\cdot1^3+2\cdot1^2-4\cdot1+1=4\)

a,

  \(A\left(x\right)=-3x^3+2x^2-6+5x+4x^3-2x^2-4-4x\\ =\left(-3x^3+4x^3\right)+\left(2x^2-2x^2\right)+\left(5x-4x\right)+\left(-6-4\right)\\ =x^3+0+x-10\\ =x^3+x-10\)

Bậc của đa thức là 3

Hệ số cao nhất ứng với x mũ lớn nhất là 1 

Thu gọn:

\(A\left(x\right)=-3x^3+2x^2-6+5x+4x^3-2x^2-4-4x\)

\(A\left(x\right)=\left(-3x^3+4x^3\right)+\left(2x^2-2x^2\right)+\left(5x-4x\right)-\left(6+4\right)\)

\(A\left(x\right)=x^3+x-10\)

Bậc của đa thức là 3

Hệ số cao nhất là 1

Ta có:

\(A\left(x\right)=-3x^3+2x^2-6+5x+4x^3-2x^2-4-4x^{ }\)

          \(=\left(-3x^3+4x^3\right)+\left(2x^2-2x^2\right)+\left(5x-4x\right)-\left(6+4\right)\)

          \(=x^3+x-10\)

Bậc của đa thức là 3, hệ số cao nhất là 1