Giúp mình Chứng minh 1+(tan^2) = 1/ (cos^2) với ạ

Những câu hỏi liên quan
a/ cot^2x-cos^2x-cot^2x.cos^2x
b/ (sin^4x+cos^4x-1).(tan^2x+cot^2x+2)
Giúp mình với ạ
Cho tam giác abc nhọn. Chứng minh: Sabc= bc^2.tan b.tan c / 2.(tan b+tan c)
giúp mình với ạ
ý của bạn là cotang đk ạ chứ mình thấy cos nó sai ý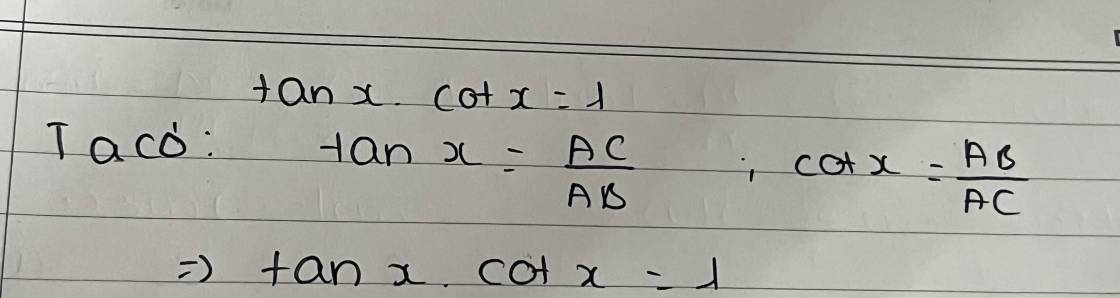
Đúng 0
Bình luận (0)
Chứng minh đẳng thức :
sin2α.tanα + cos2α.cotα+2sinα.cosα = tanα+cotα
Mọi người giúp em với ạ !!
Mình viết luôn là sin với cos, bạn tự cho thêm \(\alpha\) nhé.
VT= \(\sin^2.\dfrac{\sin}{\cos}+\cos^2.\dfrac{\cos}{\sin}+2\sin\cos\)
= \(\dfrac{\sin^3}{\cos}+\dfrac{\cos^3}{\sin}+2\sin\cos\)
= \(\dfrac{\sin^4+\cos^4+2\sin^2.\cos^2}{\cos.\sin}\)
= \(\dfrac{\left(\sin^2+\cos^2\right)^2}{\cos.\sin}\)
= \(\dfrac{1}{\sin.\cos}\)(1)
VP = \(\dfrac{\sin}{\cos}+\dfrac{\cos}{\sin}\)
= \(\dfrac{\sin^2+\cos^2}{\cos.\sin}\)
= \(\dfrac{1}{\cos.\sin}\)(2)
từ (1) và (2) => VT=VP (đpcm)
Chúc bạn học tốt!
Đúng 0
Bình luận (1)
chứng minh rằng
a) tanx(cot\(^2\)x - 1) = cotx(1 - tan\(^2\)x)
b) tan\(^2\)x - sin\(^2\)x = tan\(^2\)x.sin\(^2\)x
c) \(\dfrac{cos^2x-sin^2x}{cot^2x-tan^2x}\) - cos\(^2\)x = - cos\(^4\)x
a: tan x(cot^2x-1)
\(=\dfrac{1}{cotx}\left(cot^2x-cotx\cdot tanx\right)\)
=cotx-tanx/cotx=cotx(1-tan^2x)
b: \(tan^2x-sin^2x=\dfrac{sin^2x}{cos^2x}-sin^2x\)
\(=sin^2x\left(\dfrac{1}{cos^2x}-1\right)=sin^2x\cdot\dfrac{sin^2x}{cos^2x}=sin^2x\cdot tan^2x\)
c: \(\dfrac{cos^2x-sin^2x}{cot^2x-tan^2x}=\dfrac{cos^2x-sin^2x}{\dfrac{cos^2x}{sin^2x}-\dfrac{sin^2x}{cos^2x}}\)
\(=\left(cos^2x-sin^2x\right):\dfrac{cos^4x-sin^4x}{sin^2x\cdot cos^2x}\)
\(=\dfrac{sin^2x\cdot cos^2x}{1}=sin^2x\cdot cos^2x\)
=>sin^2x*cos^2x-cos^2x=cos^2x(sin^2x-1)
=-cos^2x*cos^2x=-cos^4x
=>ĐPCM
Đúng 1
Bình luận (0)
Chứng minh các đẳng thức:
a) \({\cos ^4}\alpha - {\sin ^4}\alpha = 2{\cos ^2}\alpha - 1\);
b) \(\frac{{{{\cos }^2}\alpha + {{\tan }^2}\alpha - 1}}{{{{\sin }^2}\alpha }} = {\tan ^2}\alpha \).
a)
Ta có:
\({\cos ^4}\alpha {\sin ^4}\alpha = \left( {{{\cos }^2}\alpha - {{\sin }^2}\alpha } \right)\left( {{{\cos }^2}\alpha + {{\sin }^2}\alpha } \right) \\= {\cos ^2}\alpha - {\sin ^2}\alpha = {\cos ^2}\alpha - (1 - {\cos ^2}\alpha ) \\= {\cos ^2}\alpha - 1 + {\cos ^2}\alpha = 2{\cos ^2}\alpha - 1\)
(đpcm)
b)
Ta có:
\(\frac{{{{\cos }^2}\alpha + {{\tan }^2}\alpha - 1}}{{{{\sin }^2}\alpha }} = \frac{{{{\cos }^2}\alpha \; + {{\tan }^2}\alpha - {{\sin }^2}\alpha - {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} \\= \frac{{{{\tan }^2}\alpha - {{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{\frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} - {{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} \\= \frac{1}{{{{\cos }^2}\alpha }} - 1 = {\tan ^2}\alpha \)
(đpcm)
Đúng 0
Bình luận (0)
Câu2: Trong ∆ vuông với góc alpha tùy ý. Chứng minh : tan alpha × cos alpha = 1.!! ( mọi người giúp em với )
Chứng minh rằng:
1) tga= sin a/ cos a 2) cotg a=cos a/ sin a
mong mn giúp mình
1) Vì \(\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{\dfrac{đối}{huyền}}{\dfrac{kề}{huyền}}=\dfrac{đối}{kề}\)
nên \(\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}\)
2) Vì \(\dfrac{\cos\alpha}{\sin\alpha}=\dfrac{\dfrac{kề}{huyền}}{\dfrac{đối}{huyền}}=\dfrac{kề}{đối}\)
nên \(\cot\alpha=\dfrac{\cos\alpha}{\sin\alpha}\)
Đúng 2
Bình luận (0)
\(\int tan\left(x\right)-ln^{15}\left(cos\left(x\right)\right)dx\)
\(\int\dfrac{x^4+x^2+1}{2x^3+5x^2-7}dx\)
tính nguyên hàm , ai giúp mình 2 bài này với hoặc 1 bài thôi cũng đc ạ , xin cảm ơn nhiều.
Chứng minh rằng: \(\frac{sin^2\alpha-cos^2\alpha}{1+2sin\alpha cos\alpha}=\frac{tan\alpha-1}{tan\alpha+1}\)
\(\frac{sin^2a-cos^2a}{sin^2a+cos^2a+2sina.cosa}=\frac{\left(sina+cosa\right)\left(sina-cosa\right)}{\left(sina+cosa\right)^2}=\frac{sina-cosa}{sina+cosa}\)
\(=\frac{\frac{sina}{cosa}-\frac{cosa}{cosa}}{\frac{sina}{cosa}+\frac{cosa}{cosa}}=\frac{tana-1}{tana+1}\)
Đúng 0
Bình luận (0)
(tan^2 a)/(1 + tan^2 a) * (1 + cot^2 a)/(cot^2 a) = (1 + tan^4 a)/(tan^2 a + tan^2 a)
Đúng 0
Bình luận (0)

















