Luyện tập – Vận dụng 3
Cho hai ví dụ về hàm số lôgarit
Luyện tập – Vận dụng 1
Cho hai ví dụ về hàm số mũ
Luyện tập – Vận dụng 7
Cho hai ví dụ về bất phương trình logarit cơ bản
Luyện tập – Vận dụng 5
Cho hai ví dụ về bất phương trình mũ cơ bản
Vận dụng mối quan hệ giữa lượng và chất hãy nêu một số ví dụ như quá trình học tập và rèn luyện của bản thân : Nhớ là ví dụ gần gũi trong học tập nha
Cho hai ví dụ về hàm số bậc hai.
Ví dụ 1: \(y = 2{x^2} - x - 1\)
Ví dụ 2: \(y = - 3{x^2} + 1\)
Hãy cho một ví dụ về hàm số được cho bằng bảng hoặc biểu đồ. Hãy chỉ ra tập xác định và tập giá trị của hàm số đó.
Ví dụ hàm số $y=\frac{-1}{2}x$
Ta có bảng sau:

Với mỗi giá trị của x ta có 1 giá trị của y, vậy bảng trên biểu thị cho 1 hàm số
Tập xác định của hàm số \(D = \left\{ { - 2; - 1; - \frac{1}{2};0;\frac{1}{2};1;2} \right\}\)
Tập giá trị của hàm số \(\left\{ {1;\frac{1}{2};\frac{1}{4};0; - \frac{1}{4}; - \frac{1}{2}; - 1} \right\}\)
Luyện tập – Vận dụng 4
Lập bảng biến thiên và vẽ đồ thị hàm số \(y = {\log _{\frac{1}{3}}}x\)
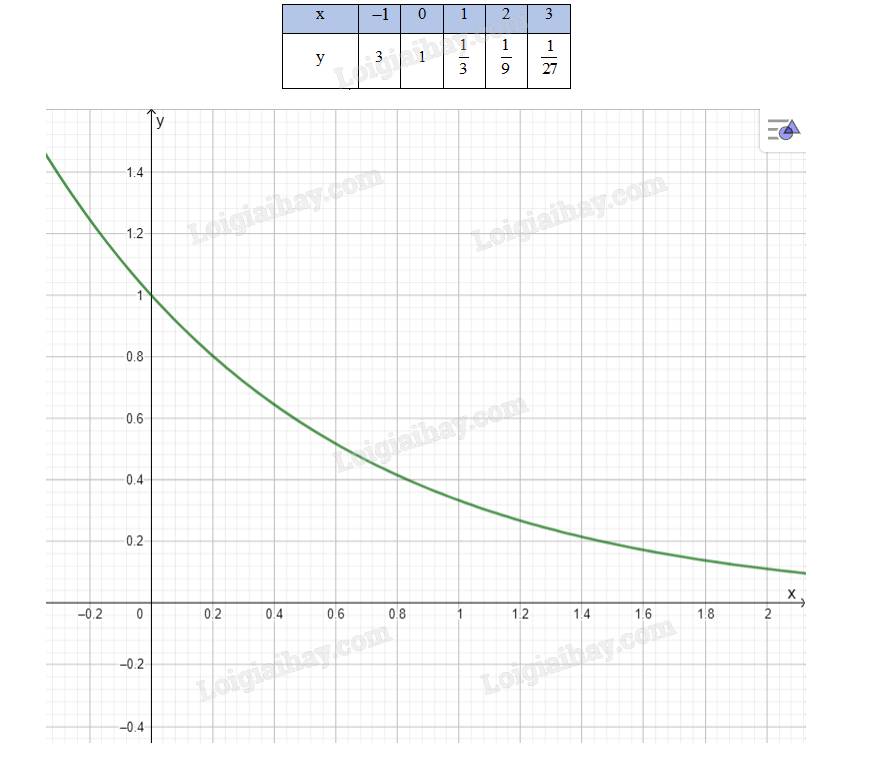
Luyện tập – Vận dụng 2
Lập bảng biến thiên và vẽ đồ thị hàm số \(y = {\left( {\frac{1}{3}} \right)^x}\)
\(\mathop {\lim }\limits_{x \to + \infty } {\left( {\frac{1}{3}} \right)^x} = 0;\,\,\mathop {\lim }\limits_{x \to - \infty } {\left( {\frac{1}{3}} \right)^x} = + \infty \)
Hàm số \(y = {\left( {\frac{1}{3}} \right)^x}\) nghịch biến trên toàn R
Bảng biến thiên của hàm số:

Đồ thị hàm số:
Hãy lấy thêm một số ví dụ về ứng dụng tập tính trong đời sống.
- Vẹt có thể nhại lại giọng người nên có thể huấn luyện chúng làm cảnh.