\(B=x^2-2x+y^2+4y+6=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1>0\forall x,y\)

\(B=x^2-2x+y^2+4y+6\)

\(=x^2-2x+1+y^2+4y+4+1\)

\(=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1>0\forall x,y\)

cho hình thang cân , đáy nhỏ AB đáy lớn CD . Góc nhọn hợp từ hai đường chéo AC và BD bằng \(60^o\)gọi M,N là hình chiếu của B và C lên AC và BD , p là trung điểm cạnh BC . Cm tam giác MNP là tam giác đều

`A=x^2 -4x+18`

`=x^2 -4x+4+14`

`=(x-2)^2 +14`

Có `(x-2)^2 >=0 AAx`

`=> (x-2)^2 +14>= 14>0 AAx`

Vậy ....

`B=x^2 -x+2`

`=x^2 -x+1/4+7/4`

`=(x-1/2)^2 +7/4`

có `(x-1/2)^2 >=0 AAx`

`=> (x-1/2)^2 +7/4>=7/4>0 AAx`

Vậy ...........

`C=x^2 +2y^2 -2xy-2y+15`

`=x^2 -2xy+y^2 +y^2 -2y+1+14`

`=(x-y)^2 +(y-1)^2 +14`

Có `(x-y)^2 >=0 AAx,y` ;   `(y-1)^2 >=0 AAy`

`=>(x-y)^2 +(y-1)^2 +14 >=14>0 AAx;y`

Vậy

B = \(x^2\) - 2\(xy\) + 2y\(^2\) + 2\(x\) - 10y + 17

B = (\(x^2\) - 2\(xy\) + y²) + 2(\(x-y\)) + 1 + (y² - 8y + 16)

B = (\(x-y\))² + 2(\(x-y\)) + 1 + (y - 4)²

B = (\(x-y\) + 1)² + (y - 4)²

(\(x-y+1\))² ≥ 0 ∀ \(x;y\); (y - 4)² ≥ 0 

B ≥ 0

Kết luận biểu thức không âm. Chứ không phải là biểu thức luôn dương em nhé. Vì dương thì biểu thức phải > 0 ∀ \(x;y\). Mà số 0 không phải là số dương. 

Giải giúp mik với mik cần gấp

Không biê

ko biết

(C₁) tâm I₁(0;2) và R₁= 3;

(C₂) tâm I₂( 3;-4) và R₂= 3

- Nhận xét : 

 không cắt C₂

- Gọi d: ax+ by+ c= 0  là tiếp tuyến chung , thế thì : d(I₁; d) = R₁ và d (I₂; d) = R₂

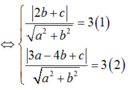
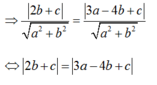
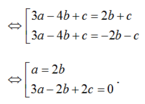
- Trường hợp: a= 2b thay vào (1):

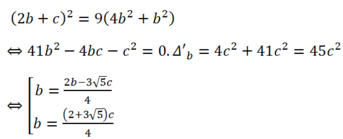
- Do đó ta có hai đường thẳng cần tìm :

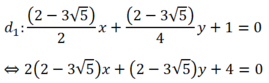
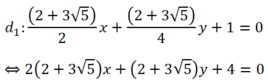
- Trường hợp : 

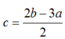
 thay vào  : 

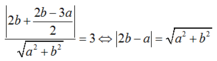
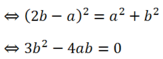
-Có 2 đường thẳng : d₃: 2x- 1 = 0 và d₄: 6x + 8y -1= 0.

Có tất cả 4 tiếp tuyến chung.

`B = x^2- 2xy + y^2 + 2x - 10y + 17

`2B = 2x^2 - 4xy + 2y^2 + 4x - 20y + 34`

`= (x-y)^2 + (x+2)^2 + (y-5)^2 + 5 >= 5`.