giải gấp giúp mình câu 3 bài 2 với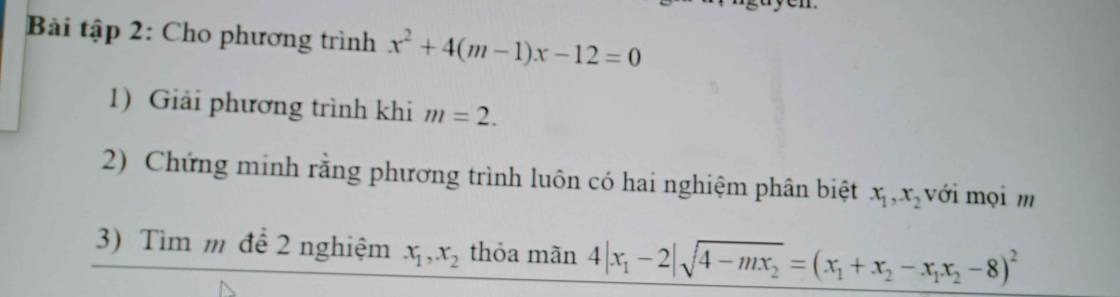

Những câu hỏi liên quan
giải giúp mình bài 4 câu 3 với cần gấp lắm ạ
a, M(x)= 3x^3 - 2x^2 + 1 (đã rút gọn ) , ý b bạn chỉ cần thay M(-1) và M(2) vào x lần lượt từng con là đc vd : M(-1)= 3* (-1^3) - 2* (- 1)^2 + 1 rồi tính ra kết quả là được
Đúng 0
Bình luận (0)
Giúp mình giải câu b,c bài hình các bài tìm GTLN , GTNN với ạ mik đang cần gấp
a) \(A=\sqrt{1-x}+\sqrt{1+x}\)
\(\Rightarrow A^2=1-x+1+x+2\sqrt{\left(1-x\right)\left(1+x\right)}=2+2\sqrt{1-x^2}\)
Do \(-x^2\le0\Rightarrow1-x^2\le1\Rightarrow A^2=2+2\sqrt{1-x^2}\le2+2=4\)
\(\Rightarrow A\le2\)
\(maxA=2\Leftrightarrow x=0\)
Áp dụng bất đẳng thức: \(\sqrt{x}+\sqrt{y}\ge\sqrt{x+y}\)(với \(x,y\ge0\))
\(\Leftrightarrow\left(\sqrt{x}+\sqrt{y}\right)^2\ge x+y\)
\(\Leftrightarrow x+y+2\sqrt{xy}\ge x+y\Leftrightarrow2\sqrt{xy}\ge0\left(đúng\right)\)
\(A=\sqrt{1-x}+\sqrt{1+x}\ge\sqrt{1-x+1+x}=\sqrt{2}\)
\(maxA=\sqrt{2}\Leftrightarrow\)\(\left[{}\begin{matrix}1-x=0\\1+x=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Đúng 0
Bình luận (1)
b: Xét ΔABE vuông tại A có AH là đường cao ứng với cạnh huyền BE
nên \(BH\cdot BE=AB^2\left(1\right)\)
Xét ΔABC vuông tại B có BH là đường cao ứng với cạnh huyền AC
nên \(AH\cdot AC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BE=AH\cdot AC\)
Đúng 0
Bình luận (0)
Đề bài mấy câu đầu là thực hiện phép tính (giải nhanh giúp mình với ạ mình đang gấp)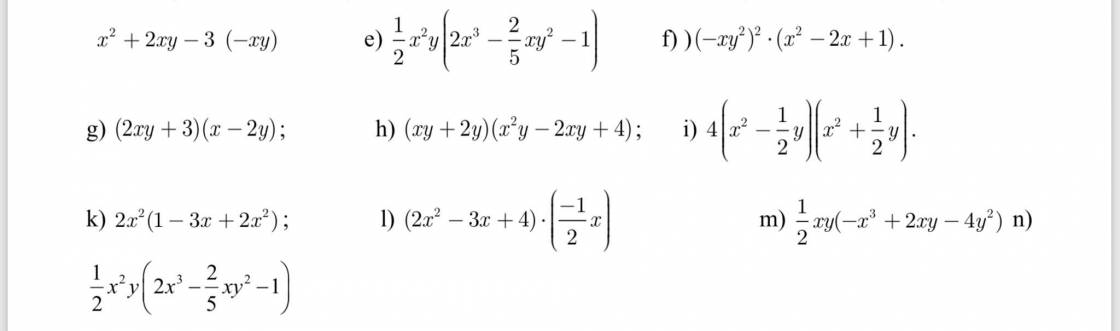
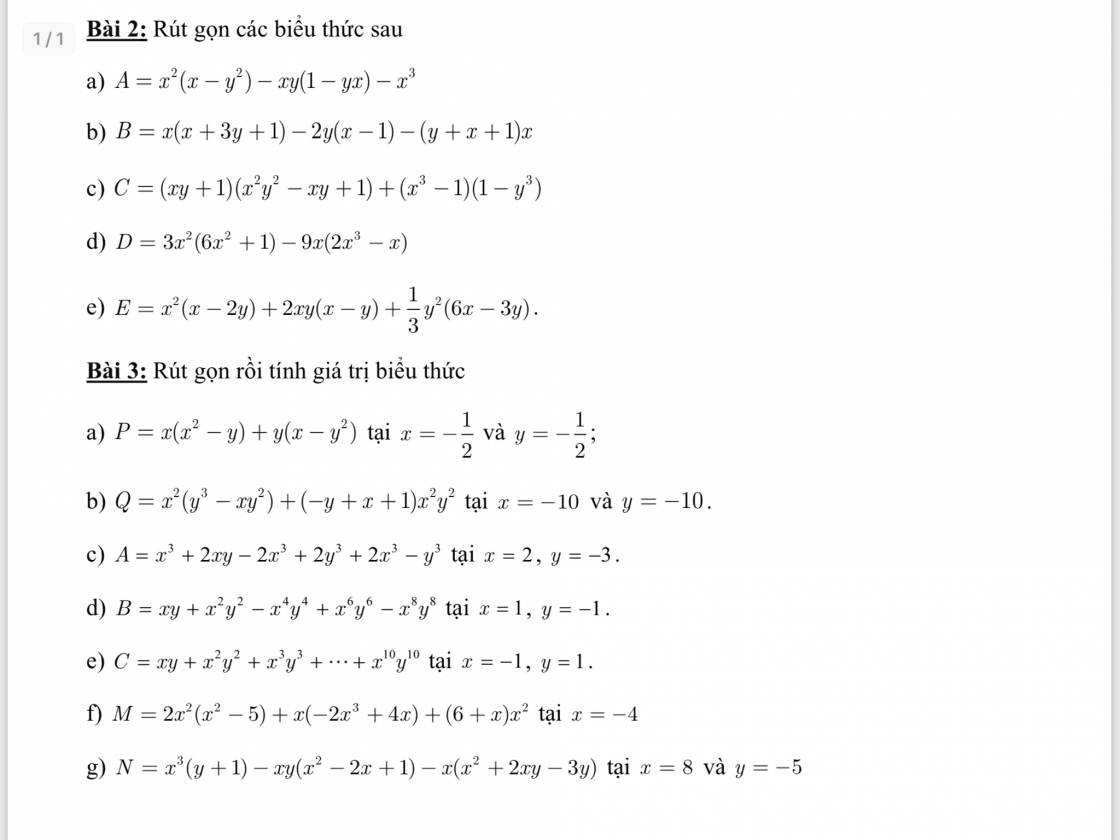
Bài 3:
a: \(P=x\left(x^2-y\right)+y\left(x-y^2\right)\)
\(=x^3-xy+xy-y^3\)
\(=x^3-y^3\)
Thay \(x=-\frac12;y=-\frac12\) vào P, ta được:
\(P=\left(-\frac12\right)^3-\left(-\frac12\right)^3=\left(-\frac18\right)-\left(-\frac18\right)=-\frac18+\frac18=0\)
b: \(Q=x^2\left(y^3-xy^2\right)+x^2y^2\left(x-y+1\right)\)
\(=x^2y^3-x^3y^2+x^3y^2-x^2y^3+x^2y^2=x^2y^2\)
Thay x=-10; y=-10 vào Q, ta được:
\(Q=\left(-10\right)^2\cdot\left(-10\right)^2=100\cdot100=10000\)
c: \(A=x^3+2xy-2x^3+2y^3+2x^3-y^3\)
\(=\left(x^3-2x^3+2x^3\right)+2xy+\left(2y^3-y^3\right)\)
\(=x^3+2xy+y^3\)
Thay x=2; y=-3 vào A, ta được:
\(A=2^3+2\cdot2\cdot\left(-3\right)+\left(-3\right)^3\)
=8-12-27
=-4-27
=-31
d:
x=1; y=-1
=>\(xy=1\cdot\left(-1\right)=-1\)
\(B=xy+x^2y^2-x^4y^4+x^6y^6-x^8y^8\)
\(=\left(xy\right)+\left(xy\right)^2-\left(xy\right)^4+\left(xy\right)^6-\left(xy\right)^8\)
\(=\left(-1\right)+\left(-1\right)^2-\left(-1\right)^4+\left(-1\right)^6-\left(-1\right)^8\)
=-1+1-1+1-1
=-1
e: x=-1; y=1
=>xy=-1
\(C=xy+x^2y^2+x^3y^3+\cdots+x^{10}y^{10}\)
\(=xy+\left(xy\right)^2+\left(xy\right)^3+\cdots+\left(xy\right)^{10}\)
\(=\left(-1\right)+\left(-1\right)^2+\left(-1\right)^3+\cdots+\left(-1\right)^{10}\)
=-1+1+(-1)+1+...+(-1)+1
=0
f: \(M=2x^2\left(x^2-5\right)+x\left(-2x^3+4x\right)+x^2\left(x+6\right)\)
\(=2x^4-10x^2-2x^4+4x^2+x^3+6x^2\)
\(=x^3\)
Khi x=-4 thì \(M=\left(-4\right)^3=-64\)
g: \(N=x^3\left(y+1\right)-xy\left(x^2-2x+1\right)-x\left(x^2+2xy-3y\right)\)
\(=x^3y+x^3-x^3y+2x^2y-xy-x^3-2x^2y+3xy\)
=2xy
Thay x=8; y=-5 vào N, ta được:
\(N=2\cdot8\cdot\left(-5\right)=-80\)
Bài 1:
d: \(x^2+2xy-3\cdot\left(-xy\right)\)
\(=x^2+2xy+3xy=x^2+5xy\)
e: \(\frac12x^2y\left(2x^3-\frac25xy^2-1\right)\)
\(=\frac12x^2y\cdot2x^3-\frac12x^2y\cdot\frac25xy^2-\frac12x^2y\)
\(=x^5y-\frac15x^3y^3-\frac12x^2y\)
f: \(\left(-xy^2\right)^2\left(x^2-2x+1\right)\)
\(=x^2y^4\left(x^2-2x+1\right)\)
\(=x^2y^4\cdot x^2-x^2y^4\cdot2x+x^2y^4\)
\(=x^4y^4-2x^3y^4+x^2y^4\)
g: (2xy+3)(x-2y)
\(=2xy\cdot x-2xy\cdot2y+3\cdot x-3\cdot2y\)
\(=2x^2y-4xy^2+3x-6y\)
h: \(\left(xy+2y\right)\left(x^2y-2xy+4\right)\)
\(=x^3y^2-2x^2y^2+4xy+2x^2y^2-4xy^2+8y\)
\(=x^3y^2+4xy-4xy^2+8y\)
i: \(4\left(x^2-\frac12y\right)\left(x^2+\frac12y\right)\)
\(=4\left(x^4-\frac14y^2\right)\)
\(=4\cdot x^4-4\cdot\frac14y^2=4x^4-y^2\)
k: \(2x^2\left(1-3x+2x^2\right)\)
\(=2x^2\cdot1-2x^2\cdot3x+2x^2\cdot2x^2\)
\(=2x^2-6x^3+4x^4\)
l: \(\left(2x^2-3x+4\right)\left(-\frac12x\right)\)
\(=-\frac12x\cdot2x^2+3x\cdot\frac12x-4\cdot\frac12x=-x^3+\frac32x^2-2x\)
m: \(\frac12xy\left(-x^3+2xy-4y^2\right)\)
\(=-\frac12xy\cdot x^3+\frac12xy\cdot2xy-\frac12xy\cdot4y^2\)
\(=-\frac12x^4y+x^2y^2-2xy^3\)
n: \(\frac12x^2y\left(2x^3-\frac25xy^2-1\right)\)
\(=\frac12x^2y\cdot2x^3-\frac12x^2y\cdot\frac25xy^2-\frac12x^2y\)
\(=x^5y-\frac15x^3y^3-\frac12x^2y\)
Đúng 0
Bình luận (0)
Giúp mình giải câu b bài 2 đc ko ạ, mình cần gấp lắm rồi
b: \(\dfrac{2x^3-3x^2+6x-9}{2x-3}=x^2+3\)
Đúng 1
Bình luận (0)

Giúp mình câu 3 bài 3 với, mình đang cần gấp ạ
3:
c: Xét ΔCAM có KI//AM
nên KI/AM=CI/CM
Xét ΔCMB có HI//MB
nên HI/MB=CI/CM
=>KI/AM=HI/MB
=>KI=HI
=>I là trung điểm của HK
Đúng 0
Bình luận (0)
Giải gấp giúp mình 2 bài này với ạ, sáng mai mình nộp rồi. Giúp mình với ạ
Bài 5:
a: BC=10cm
b: HA=4,8cm
HB=3,6(cm)
HC=6,4(cm)
Đúng 0
Bình luận (1)
Bài 6:
\(x^3=6+3\sqrt[3]{\left(3+2\sqrt{2}\right)\left(3-2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\\ \Leftrightarrow x^3=6+3x\sqrt[3]{1}\\ \Leftrightarrow x^3-3x=6\\ y^3=34+3\sqrt[3]{\left(17+12\sqrt{2}\right)\left(17-12\sqrt{2}\right)}\left(\sqrt[3]{17+12\sqrt{2}}+\sqrt[3]{17-12\sqrt{2}}\right)\\ \Leftrightarrow y^3=34+3y\sqrt[3]{1}\\ \Leftrightarrow y^3-3y=34\\ \Leftrightarrow P=x^3-3x+y^3-3y+1980=6+34+1980=2020\)
Đúng 0
Bình luận (0)

Giúp mình 3 câu cuối cùng của bài 1 và bài 2 với ạ mình đng cần khá gấp hạn cuối là 15h chiều Hnay ạ
`@` `\text {Ans}`
`\downarrow`

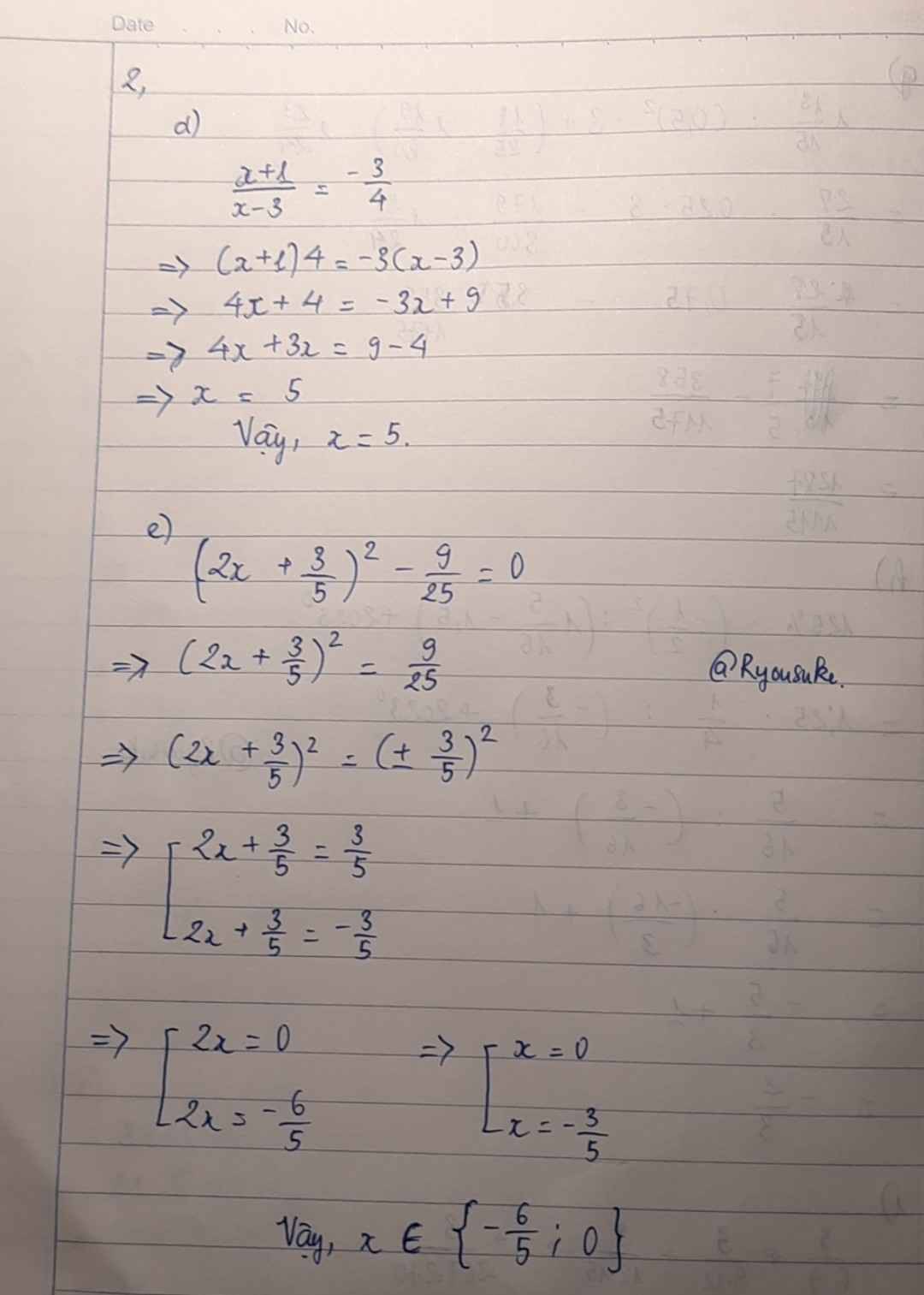
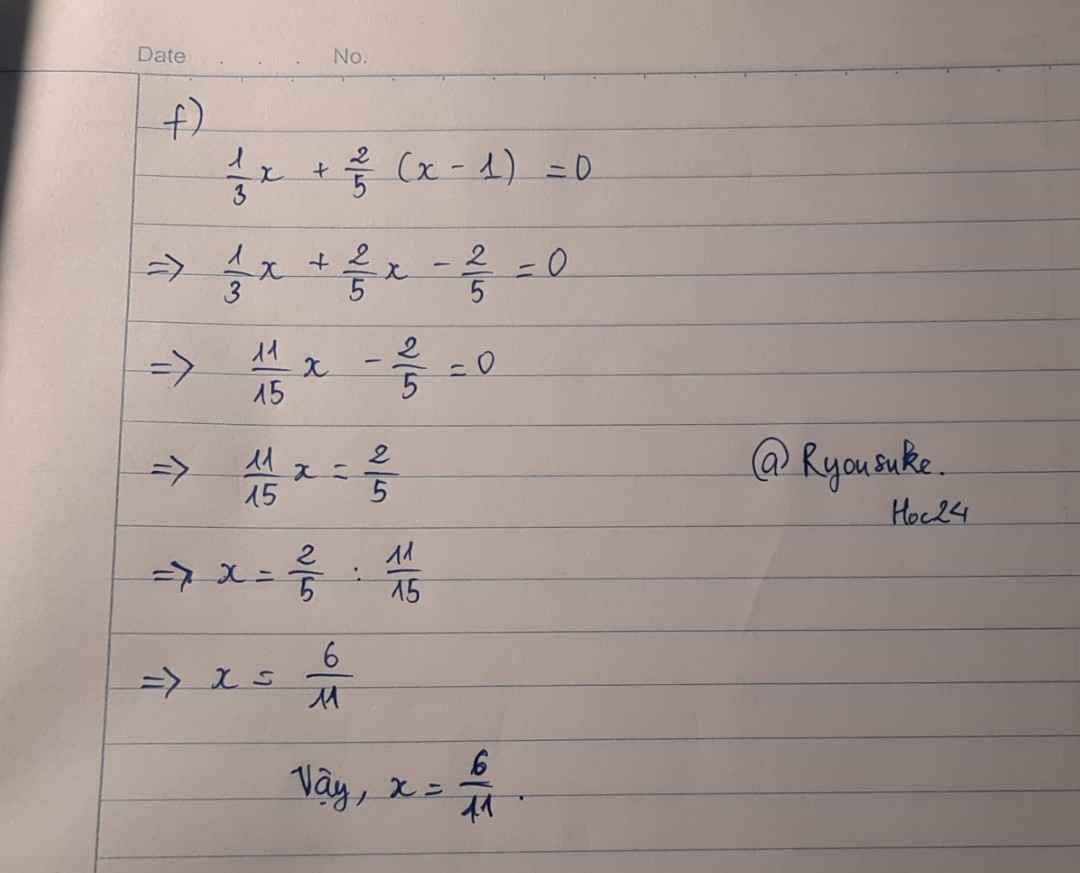
Đúng 2
Bình luận (0)
giúp mình bài 1 và 2 với mình đang cần gấp. giải ra giúp mình nha

1:
a: =12/10-7/10=5/10=1/2
b: \(=\dfrac{4}{13}-\dfrac{4}{13}+\dfrac{-5}{11}-\dfrac{6}{11}=-\dfrac{11}{11}=-1\)
2:
a: x+2/7=-11/7
=>x=-11/7-2/7=-13/7
b: (x+3)/4=-7/2
=>x+3=-14
=>x=-17
Đúng 0
Bình luận (0)
Giúp mình 1 trong 2 bài này với ạ. Nếu được thì giải 2 bài này giúp mk với. Mình đang cần gấp lắm ạ 😢
jimmmmmmmmmmmmmmmmmmmmmmmmmmm
he he he he he he
bài 1:
bn lấy giá trị của √(4^2-3,9^2) là dc
bài 2
AB+BC=2√(3^2+4^2)=??
Xem thêm câu trả lời























