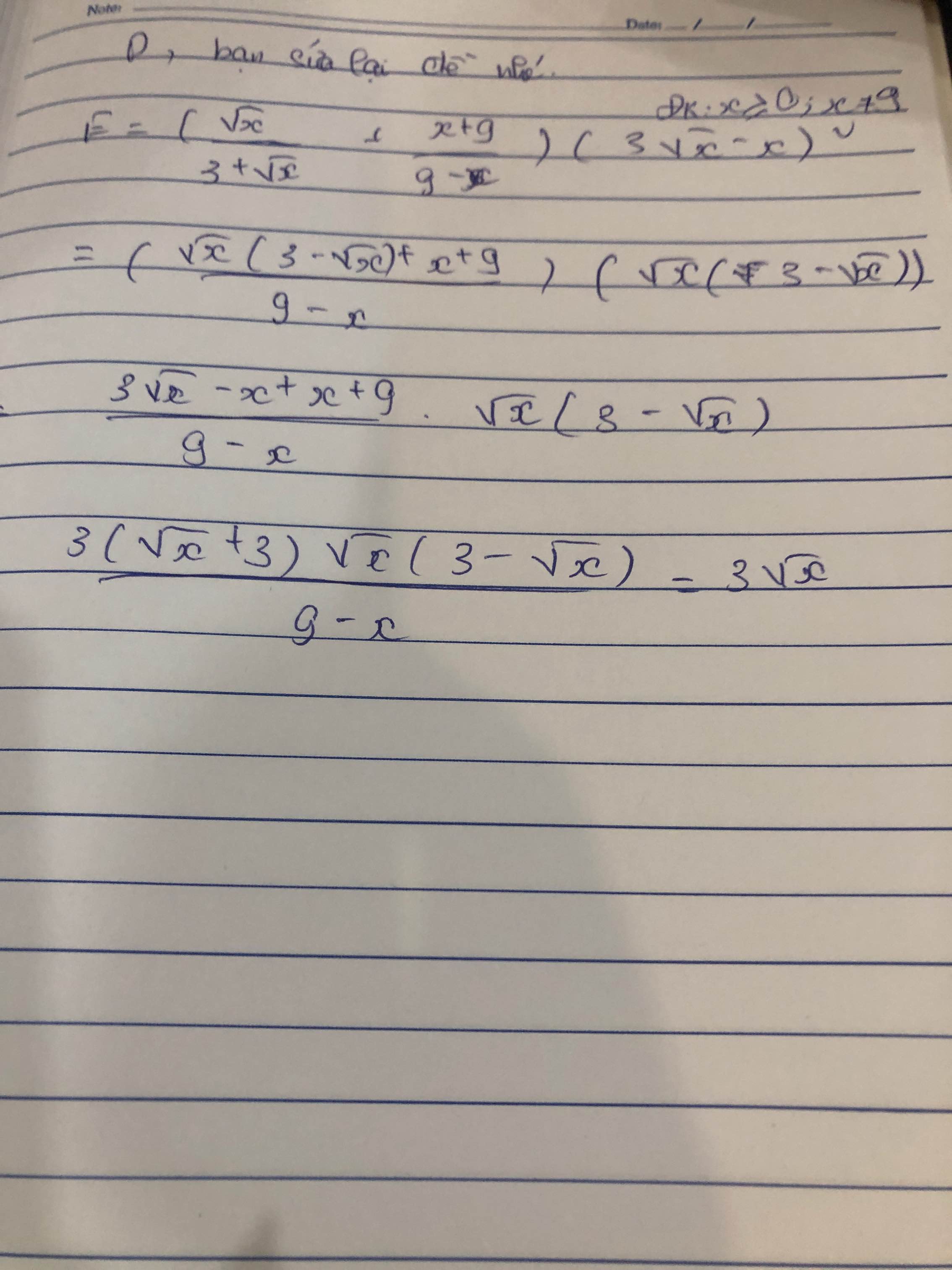\(=9\sqrt{x}-9.\dfrac{1}{3}.\sqrt{x}+x.\dfrac{1}{\sqrt{x}}.\sqrt{9}-3x\)

\(=9\sqrt{x}-3\sqrt{x}+3\sqrt{x}-3x\)

\(=-3x+9\sqrt{x}\)

\(=9\sqrt{x}-9\cdot\dfrac{1}{3}\sqrt{x}+3\sqrt{\dfrac{x^2}{x}}-x\sqrt{9}\\ =9\sqrt{x}-3\sqrt{x}+3\sqrt{x}-3x\\ =9\sqrt{x}-3x=3\sqrt{x}\left(3\sqrt{x}-1\right)\)

a: Ta có: \(A=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}-\dfrac{3}{\sqrt{x}+2}+\dfrac{12}{x-4}\)

\(=\dfrac{x+4\sqrt{x}+4-3\sqrt{x}+6+12}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)

\(=\dfrac{x+\sqrt{x}+22}{x-4}\)

d: Ta có: \(D=\dfrac{1}{\sqrt{x}+3}-\dfrac{\sqrt{x}}{3-\sqrt{x}}+\dfrac{2\sqrt{x}-12}{x-9}\)

\(=\dfrac{\sqrt{x}-3+x+3\sqrt{x}+2\sqrt{x}-12}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{x+6\sqrt{x}-15}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)

A=\(A=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}-\dfrac{3}{\sqrt{x}+2}+\dfrac{12}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}A=\dfrac{\sqrt{x}+2.\left(\sqrt{x}+2\right)-3.\left(\sqrt{x}-2\right)+12}{\left(\sqrt{x}-2\right).\left(\sqrt{x}+2\right)}A=\dfrac{\sqrt{x}+2\sqrt{x}+4-3\sqrt{x}+6+12}{\left(\sqrt{x}-2\right).\left(\sqrt{x}+2\right)}A=\dfrac{22}{\left(\sqrt{x}-2\right).\left(\sqrt{x}+2\right)}\)

1.

\(A=\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{x+9\sqrt{x}}{9-x}\)

\(=\dfrac{2\sqrt{x}}{\sqrt{x}+3}-\dfrac{x+9\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}-\dfrac{x+9\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{2x-6\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}-\dfrac{x+9\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{x-15\sqrt{x}}{x-9}\)

2.

\(B=\dfrac{3}{\sqrt{x}-3}+\dfrac{2}{\sqrt{x}+3}+\dfrac{x-5\sqrt{x}-3}{x-9}\)

\(=\dfrac{3\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+\dfrac{2\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+\dfrac{x-5\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{3\sqrt{x}+9+2\sqrt{x}-6+x-5\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{x}{x-9}\)

3.

\(C=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{x+\sqrt{x}}{x-1}\)

\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)

\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}}{\sqrt{x}-1}\)

\(=\dfrac{1}{\sqrt{x}-1}\)

\(=\left(\dfrac{x+9}{x-9}-\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{x-9}\right).\dfrac{x-3\sqrt{x}}{\sqrt{x}}\\ =\left(\dfrac{x+9-x+3\sqrt{x}}{x-9}\right).\dfrac{x-3\sqrt{x}}{\sqrt{x}}\\ =\dfrac{3\left(3+\sqrt{x}\right)}{\left(\sqrt{x}-3\right)\left(3+\sqrt{x}\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\sqrt{x}}\\ =3\)

d) \(\sqrt{x^2-6x+9}=2\Leftrightarrow\sqrt{\left(x-3\right)^2}=2\Leftrightarrow x-3=2\Leftrightarrow x=5\)

e) đk: \(x\ge2\)\(\sqrt{x^2-3x+2}=\sqrt{x-1}\Leftrightarrow\sqrt{\left(x-2\right)\left(x-1\right)}=\sqrt{x-1}\Leftrightarrow\sqrt{x-2}=1\Leftrightarrow x-2=1\Leftrightarrow x=3\)f) \(\sqrt{4x^2-4x+1}=\sqrt{x^2-6x+9}\Leftrightarrow\sqrt{\left(2x-1\right)^2}=\sqrt{\left(x-3\right)^2}\Leftrightarrow2x-1=x-3\Leftrightarrow x=-2\)

c: Ta có: \(\sqrt{x+4\sqrt{x-4}}=2\)

\(\Leftrightarrow\left|\sqrt{x-4}+2\right|=2\)

\(\Leftrightarrow x-4=0\)

hay x=4

a) \(\sqrt{x-1+2\sqrt{x-1}.1+1^2}=2;đk:x\)≥1
⇔\(\sqrt{\left(\sqrt{x-1}\right)^2+2\sqrt{x-1}.1+1^2}=2\left(hđt-1\right)\)
⇔\(\sqrt{\left(\sqrt{x-1}+1\right)^2=2}\)
⇔|\(\sqrt{x-1}+1\)|=2
⇔\(\left[{}\begin{matrix}\sqrt{x+1}-1=2\\\sqrt{x+1-1}=-2\end{matrix}\right.\)⇔\(\left[{}\begin{matrix}\sqrt{x+1}=3\\\sqrt{x+1}=-1\left(L\right)\end{matrix}\right.\)⇔x+1=9⇔x=10(TM)
→S={10}

\(\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{x+6\sqrt{x}+9}{9-x}-\dfrac{\sqrt{x}}{\sqrt{x}+3}\left(dkxd:x\ge0,x\ne9\right)\)

\(=\dfrac{2\sqrt{x}}{\sqrt{x}+3}-\dfrac{\left(\sqrt{x}+3\right)^2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{\sqrt{x}}{\sqrt{x}+3}\)

\(=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)-\left(x+6\sqrt{x}+9\right)-\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{2x-6\sqrt{x}-x-6\sqrt{x}-9-x+3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{-9\sqrt{x}-9}{x-9}\) với \(x\ge0,x\ne9\)

\(\left(\dfrac{1}{\sqrt{x}-3}-\dfrac{\sqrt{x}}{x-9}\right)\cdot\left(\sqrt{x}+\dfrac{\sqrt{x}-9}{\sqrt{x}-1}\right)\left(đk:x\ge0;x\ne9;x\ne1\right)\)

\(=\left[\dfrac{\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\right]\cdot\left[\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}+\dfrac{\sqrt{x}-9}{\sqrt{x}-1}\right]\)

\(=\dfrac{\sqrt{x}+3-\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{x-\sqrt{x}+\sqrt{x}-9}{\sqrt{x}-1}\)

\(=\dfrac{3}{x-9}\cdot\dfrac{x-9}{\sqrt{x}-1}\)

\(=\dfrac{3}{\sqrt{x}-1}\)