Cho 3 đường thẳng a,b,c biết a song song b song song c. Gọi A thuộc a, D thuộc a và đi qua a. Hỏi D có cắt b,c không? Vì sao?

Những câu hỏi liên quan
vẽ hình theo cách diễn đạt sau :
a, vẽ hai đường thẳng phân biệt ko song song a và b
b,lấy 2 điểm A và B sao cho A thuộc a ,B thuộc b
c, vẽ đường thẳng C đi qua B sao cho c vuông góc với a
d,Vẽ đường thẳng d đi qua A sao cho d song song với b
Cho hàm số bậc nhất y = (2 - a)x + a (d). Biết đồ thị (d) của hàm số đi qua điểm M(3;1).
a) Hàm số đồng biến hay nghịch biến trên R? Vì sao?
b) Điểm A(-1;3) có thuộc (d) không?
c) Viết phương trình đường thẳng (d') biết (d') song song với (d) và đi qua trung điểm đoạn MN, biết N(-1;5).
Lời giải:
a. Vì $(d)$ đi qua $M(3;1)$ nên:
$y_M=(2-a)x_M+a$
$\Leftrightarrow 1=(2-a).3+a\Rightarrow a=2,5$
Khi đó: $y=(2-2,5)x+2,5=-0,5x+2,5$
Vì $-0,5<0$ nên hàm nghịch biến trên R.
b.
$y_A=3$
$-0,5x_A+2,5=-0,5.(-1)+2,5=3$
$\Rightarrow y_A=-0,5x_A+2,5$ nên điểm $A\in (d)$
c. Gọi PTĐT $(d')$ là: $y=mx+n$ với $m,n$ là số thực
$(d')\parallel (d)$ nên $m=-0,5$
$M(3;1), N(-1,5)\Rightarrow$ tọa độ trung điểm $I$ của $MN$ là:
$(\frac{3-1}{2}; \frac{1+5}{2})=(1,3)$
$(d')$ đi qua $(1,3)$ nên:
$3=m.1+n\Rightarrow m+n=3\Rightarrow n=3-m=3-(-0,5)=3,5$
Vậy PTĐT $(d')$ là: $y=-0,5x+3,5$
Đúng 3
Bình luận (0)
Cho tam giác ABC đều, M là một điểm thuộc miền của tam giác. Qua M kẻ đường thẳng song song với BC cắt AB ở D, đường thẳng song song với AC cắt BC ở E, đường thẳng song song với AB cắt AC ở F.
a) Có bao nhiêu hình thang cân tất cả? Vì sao?
b) Cho biết MA = a, MB = b, MC = c. Chứng minh 3 đoạn thẳng MA, MB, MC thỏa mãn bất đẳng thức tam giác và tính chu vi tam giác DEF theo a, b, c.
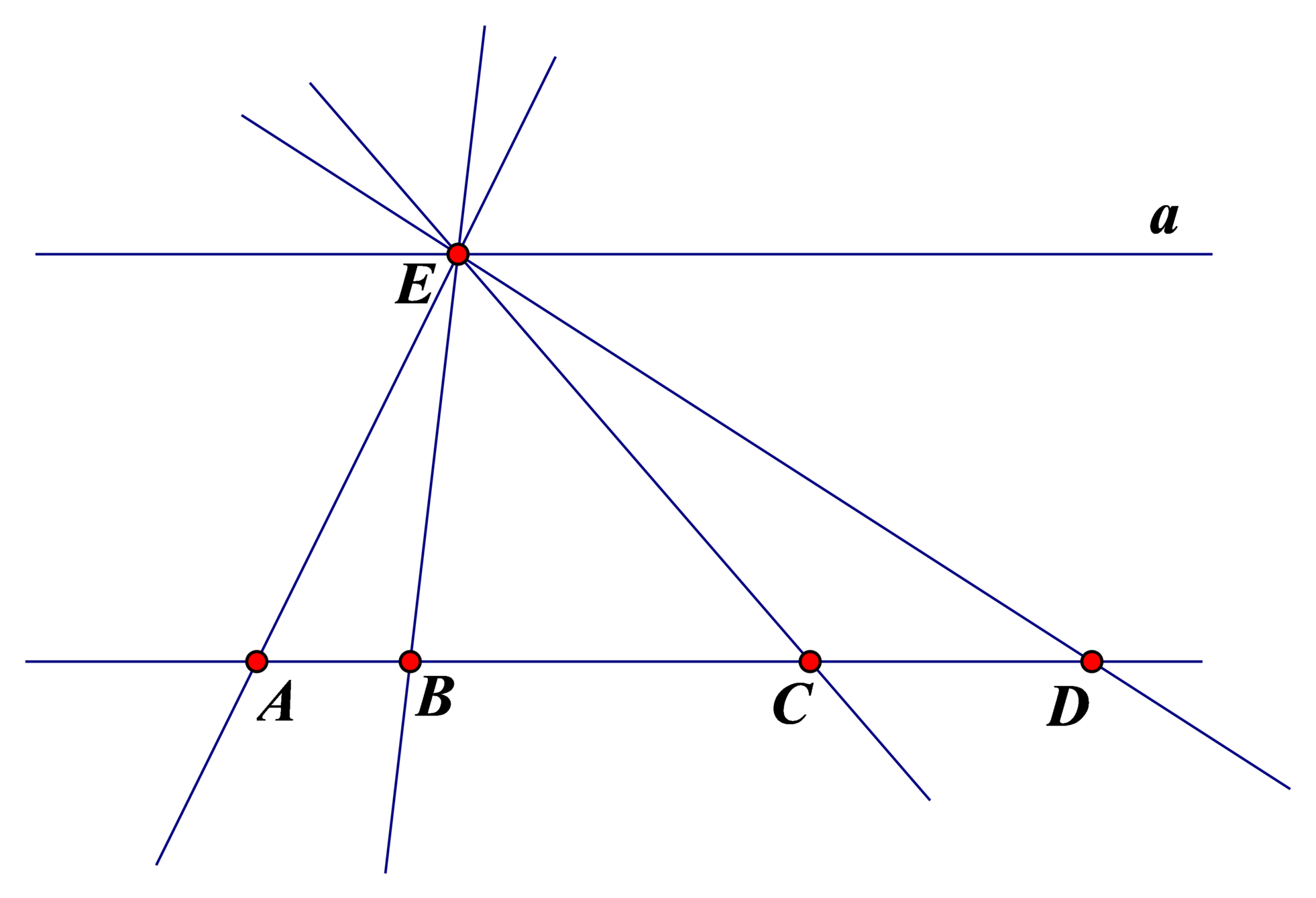
Vẽ hình theo các bước diễn đạt sau:- Vẽ năm điểm phân biệt A, B, C, D, E sao cho ba điểm A, B, C thẳng hàng; ba điểm B, C, D thẳng hàng; ba điểm B, C, E không thẳng hàng;- Vẽ các đường thẳng đi qua các cặp điểm. Có bao nhiêu đường thảng phân biệt trong hình vẽ?- Vẽ đường thẳng a đi qua điểm e và song song với đường thẳng AB. Hỏi đường thẳng a có cắt đường thẳng CD không? Vì sao?
Đọc tiếp
Vẽ hình theo các bước diễn đạt sau:
- Vẽ năm điểm phân biệt A, B, C, D, E sao cho ba điểm A, B, C thẳng hàng; ba điểm B, C, D thẳng hàng; ba điểm B, C, E không thẳng hàng;
- Vẽ các đường thẳng đi qua các cặp điểm. Có bao nhiêu đường thảng phân biệt trong hình vẽ?
- Vẽ đường thẳng a đi qua điểm e và song song với đường thẳng AB. Hỏi đường thẳng a có cắt đường thẳng CD không? Vì sao?
- Có năm đường thảng phân biệt trong hình vẽ, đó là: EA , EB , EC , ED , AB .
- Hai đường thẳng AB và CD trùng nhau; đường thẳng a song song với đường thẳng AB nên cũng song song với đường thẳng CD. Do đó, đường thẳng a không cắt đường thẳng CD.
Đúng 0
Bình luận (0)
Cho đường tròn (O) tâm O đường kính AB. Gọi tia Aa là tiếp truyến của đường tròn (O) tại tiếp điểm A. Lấy điểm C thuộc tia Aa sao cho C không trùng A. Đường thẳng qua B song song với đường thẳng OC cắt đường tròn (O) tại D, với D không trùng B. Gọi I là giao điểm của hai đường thẳng OC và AD. 1) Chứng minh I là trung điểm của đoạn AD. Chứng minh OC vuông góc với đường thẳng AD. 2) Chứng minh CD là tiếp tuyến của đường tròn (O) Giúp mình với!!
Đọc tiếp
Cho đường tròn (O) tâm O đường kính AB. Gọi tia Aa là tiếp truyến của đường tròn (O) tại tiếp điểm A. Lấy điểm C thuộc tia Aa sao cho C không trùng A. Đường thẳng qua B song song với đường thẳng OC cắt đường tròn (O) tại D, với D không trùng B. Gọi I là giao điểm của hai đường thẳng OC và AD.
1) Chứng minh I là trung điểm của đoạn AD. Chứng minh OC vuông góc với đường thẳng AD.
2) Chứng minh CD là tiếp tuyến của đường tròn (O)
Giúp mình với!!
cho đường tròn tâm O đường kính AB. gọi tia Aa là tiếp tuyến của đường tròn O tại tiếp điểm A. lấy điểm C thuộc tia Aa sao cho C không trùng A. Đường thẳng qua B song song với đường thẳng OC cắt đường tròn O tại điểm D, với D không trùng B. gọi I là giao điểm của hai đường thẳng OCvà AD1) chứng minh I là trung điểm của đoạn AD. chứng minh đường thẳng OC vuông góc với đường thẳng AD.2)chứng minh CD là tiếp tuyến của đường tròn Ovẽ hình giúp mình giùm nha cảm ơn :v
Đọc tiếp
cho đường tròn tâm O đường kính AB. gọi tia Aa là tiếp tuyến của đường tròn O tại tiếp điểm A. lấy điểm C thuộc tia Aa sao cho C không trùng A. Đường thẳng qua B song song với đường thẳng OC cắt đường tròn O tại điểm D, với D không trùng B. gọi I là giao điểm của hai đường thẳng OCvà AD
1) chứng minh I là trung điểm của đoạn AD. chứng minh đường thẳng OC vuông góc với đường thẳng AD.
2)chứng minh CD là tiếp tuyến của đường tròn O
vẽ hình giúp mình giùm nha cảm ơn :v
1: Xét ΔBDA có
O là trung điẻm của AB
OI//BD
=>I là trung điểm của AD
ΔOAD cân tại O
mà OI là trung tuyến
nên OI vuông góc AD và OI là phân giác của góc AOD
2: Xét ΔOAC và ΔODC có
OA=OD
góc AOC=góc DOC
OC chung
Do đó: ΔOAC=ΔODC
=>góc ODC=90 độ
=>CD là tiếp tuyến của (O)
Đúng 0
Bình luận (0)
Cho 3 đường thẳng phân biệt a, b, c biết rằng a song song với c và b song song với c. Gọi A là một điểm nào đó trên đường thẳng a. d là một đường thẳng khác đường thẳng a và đi qua điểm A. Đường thẳng d có cắt hai đường thẳng b và c không? Vì sao?
Ba đường thẳng a, b, c phân biệt mà a // b và b // c nên a // b.
Theo tiên đề Euclid, qua điểm A chỉ có một đường thẳng song song với đường thẳng b. Mà đó chính là đường thẳng a. Do đó nếu đường thẳng d khác đường thẳng a thì đường thẳng d không song song với đường thẳng b, tức là đường thẳng d cắt đường thẳng b. Tương tự, đường thẳng d cắt đường thẳng c.
Đúng 0
Bình luận (0)
Sửa lại chút bài làm của mình:
Ba đường thẳng a, b, c phân biệt mà a // c và b // c nên a // b.
Phần còn lại không cần sửa, mình nghĩ thế.
Đúng 0
Bình luận (1)
Có. vì a song song với c và b song song với c suy ra a song song với b.
Mà đường thẳng d đi qua điểm A nằm trên dt a suy ra đường thẳng d có cắt hai đường thẳng b và c.
Đúng 0
Bình luận (0)
Cho ba đường thẳng song song a,b,c. Gọi d là đường thẳng cắt a nhưng không cắt b và c. Xét đường thẳng D cắt d và song song với b. Khẳng định nào sau đây đúng? A.
∆
⊂
m
p
a
,
d
B.
∆
⊂
m
p
a
,
b
C.
∆
⊂
m
p
a...
Đọc tiếp
Cho ba đường thẳng song song a,b,c. Gọi d là đường thẳng cắt a nhưng không cắt b và c. Xét đường thẳng D cắt d và song song với b. Khẳng định nào sau đây đúng?
A. ∆ ⊂ m p a , d
B. ∆ ⊂ m p a , b
C. ∆ ⊂ m p a , c
D. ∆ ⊂ m p b , c
cho tam giác ABc không cân . Gọi E là trung điểm của AB, F thuộc AC sao cho EF song song với BC và EF=3cm
a, Tính BC
b, Qua A kẻ đường thẳng d song song với BC. Lấy điểm D thuộc d sao cho AD=10cm và D thuộc nửa mặt phẳng có bờ AB chưa điểm C. Đường thẳng EF cắt CD tại I. Tính EI
c, Kẻ AH vuông góc với BC tại H. Gọi M là trung điểm của BC. Chứng minh HMFE là hình thang cân
















