Đề sai nha bn, mk sửa lại chút xíu ở số cuối của A là 1²

A = 100² - 99² + 98² - 97² + ... + 2² - 1²

A = (100 - 99).(100 + 99) + (98 - 97).(98 + 97) + ... + (2 - 1).(2 + 1)

A = 1.(100 + 99) + 1.(98 + 97) + ... + 1.(2 + 1)

A = 100 + 99 + 98 + 97 + ... + 2 + 1

A = (100 + 1).100:2

A = 101.50

A = 5050

a) Ta có: \(P=\dfrac{15\sqrt{x}-11}{x+2\sqrt{x}-3}+\dfrac{3\sqrt{x}-2}{1-\sqrt{x}}-\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}\)

\(=\dfrac{15\sqrt{x}-11-\left(3\sqrt{x}-2\right)\left(\sqrt{x}+3\right)-\left(2\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)

\(=\dfrac{15\sqrt{x}-11-3x-9\sqrt{x}+2\sqrt{x}+6-2x+2\sqrt{x}-3\sqrt{x}+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)

\(=\dfrac{-5x+7\sqrt{x}-2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)

\(=\dfrac{-\left(5\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)

\(=\dfrac{-5\sqrt{x}+2}{\sqrt{x}+3}\)

b) Để P nguyên thì \(-5\sqrt{x}+2⋮\sqrt{x}+3\)

\(\Leftrightarrow17⋮\sqrt{x}+3\)

\(\Leftrightarrow\sqrt{x}+3=17\)

\(\Leftrightarrow\sqrt{x}=14\)

hay x=196

Đkxđ : \(x\ne3;-3\)

Ta có :

\(\frac{4x^2-24x+36}{x^2-9}\)

\(=\frac{4\left(x^2-6x+9\right)}{x^2-3^2}\)

\(=\frac{4\left(x^2-2.3.x+3^2\right)}{\left(x-3\right)\left(x+3\right)}\)

\(=\frac{4\left(x-3\right)^2}{\left(x-3\right)\left(x+3\right)}\)

\(=\frac{4\left(x-3\right)}{x+3}\)

4

\(A=\dfrac{\sqrt{2}.cosx-2cos\left(\dfrac{\pi}{4}+x\right)}{-\sqrt{2}.sinx+2sin\left(\dfrac{\pi}{4}+x\right)}\)

\(=\dfrac{\sqrt{2}.cosx-2\left(cos\dfrac{\pi}{4}.cosx-sin\dfrac{\pi}{4}.sinx\right)}{-\sqrt{2}.sinx+2\left(sin\dfrac{\pi}{4}.cosx+cos\dfrac{\pi}{4}.sinx\right)}\)

\(=\dfrac{\sqrt{2}.cosx-\sqrt{2}.cosx+\sqrt{2}.sinx}{-\sqrt{2}.sinx+\sqrt{2}.cosx+\sqrt{2}.sinx}\)

\(=\dfrac{\sqrt{2}.sinx}{\sqrt{2}.cosx}=tanx\)

a) \(=\left[\left(x+1\right)^2-2\left(x+1\right)\left(x-1\right)+\left(x-1\right)^2\right]-\left(x+1\right)\left(x-1\right)-2\left(x-1\right)^2=\left(x+1-x+1\right)^2-\left(x-1\right)\left(x+1+2x-2\right)\)\(=4-\left(x+1\right)\left(3x-1\right)\)

b) câu này xem lại đề đi. khó hiểu quá

ko biết

c/đễ A<0  <=>  -1/X-2 <0  <=> x-2<0  <=>x<2 

a)  \(A=\left(\frac{x}{x^2-4}+\frac{2}{2-x}+\frac{1}{x+2}\right):\left(x-2+\frac{10-x^2}{x+2}\right)\)

\(ĐKXĐ:x\ne\pm2\)

\(A=\left(\frac{x}{x^2-4}-\frac{2}{x-2}+\frac{1}{x+2}\right):\left(\frac{x^2-4}{x+2}+\frac{10-x^2}{x+2}\right)\)

\(A=\left(\frac{x}{x^2-4}-\frac{2\left(x+2\right)}{x^2-4}+\frac{x-2}{x^2-4}\right):\frac{6}{x+2}\)

\(A=\frac{x-2\left(x+2\right)+x-2}{x^2-4}:\frac{6}{x+2}\)

\(A=\frac{-6}{x^2-4}:\frac{6}{x+2}\)

\(A=\frac{-6}{\left(x-2\right)\left(x+2\right)}\times\frac{x+2}{6}\)

\(A=\frac{-1}{x-2}\)

b) Ta có \(\left|x\right|=\frac{1}{2}\Leftrightarrow x=\pm\frac{1}{2}\)

TH1: Nếu \(x=\frac{1}{2}\)thì:

\(A=\frac{-1}{\frac{1}{2}-2}=\frac{-1}{\frac{-3}{2}}=-1\times\frac{2}{-3}=\frac{2}{3}\)

TH2: nếu \(x=\frac{-1}{2}\)thì:

\(A=\frac{-1}{\frac{-1}{2}-2}=\frac{-1}{\frac{-5}{2}}=-1\times\frac{2}{-5}=\frac{2}{5}\)

Vậy tại \(\left|x\right|=\frac{1}{2}\)thì \(A=\left\{\frac{2}{3};\frac{2}{5}\right\}\)

c) Để \(A< 0\)thì \(\frac{-1}{x-2}< 0\)

\(\Leftrightarrow x-2>0\)

\(\Leftrightarrow x>2\)

Vậy để \(A< 0\)thì \(x>2\)

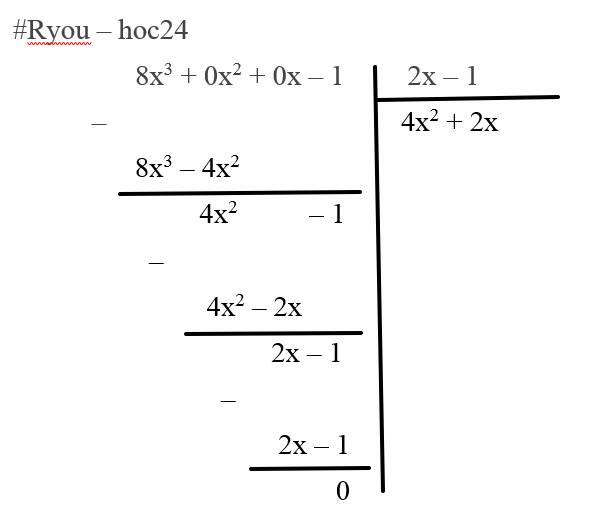
=(2x-1)(4x^2+2x+1):(2x-1)

=4x^2+2x+1

`@` `\text {Ans}`

`\downarrow`