c) \(\sqrt{\left(x-2\right)^2}+\dfrac{x-2}{\sqrt{\left(x-2\right)^2}}\)
\(=\left|x-2\right|+\dfrac{x-2}{\left|x-2\right|}\)
TH1: \(\left|x-2\right|=-\left(x-2\right)\) với \(x< 2\)
\(\Rightarrow-\left(x-2\right)+\dfrac{x-2}{-\left(x-2\right)}=-x+2-1=-x+1\)
TH2: \(\left|x-2\right|=x-2\) với \(x\ge2\)
\(\Rightarrow x-2+\dfrac{x-2}{x-2}=x-2+1=x-1\)
d) \(\sqrt{a}-\sqrt{a-2\sqrt{a}+1}\)
\(=\sqrt{a}-\sqrt{\left(\sqrt{a}\right)^2-2\cdot\sqrt{a}\cdot1-1^2}\)
\(=\sqrt{a}-\sqrt{\left(\sqrt{a}-1\right)^2}\)
\(=\sqrt{a}-\left|\sqrt{a}-1\right|\)
TH1: \(\left|\sqrt{a}-1\right|=-\left(\sqrt{a}-1\right)\) với \(a< 1\)
\(\Rightarrow\sqrt{a}-\left[-\left(\sqrt{a}-1\right)\right]=\sqrt{a}+\sqrt{a}-1=2\sqrt{a}-1\)
TH2: \(\left|\sqrt{a}-1\right|=\sqrt{a}-1\) với \(a\ge1\)
\(\Rightarrow\sqrt{a}-\left(\sqrt{a}-1\right)=\sqrt{a}-\sqrt{a}+1=1\)

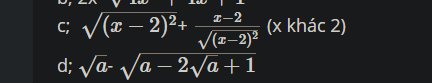






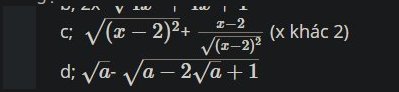




![[MINT HANOUE]](https://hoc24.vn/images/avt/avt83544866_256by256.jpg)