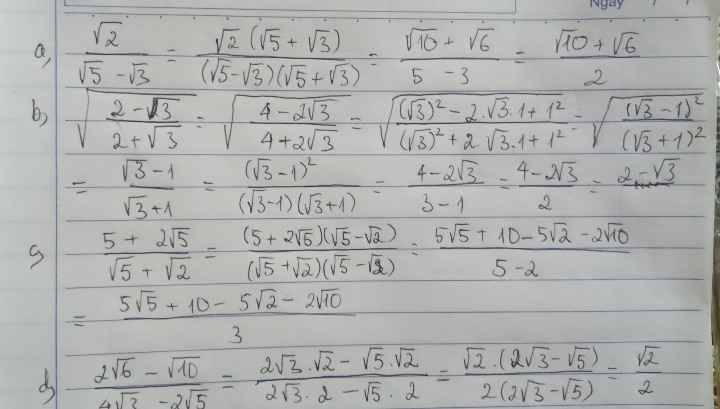Trước hết, ta cần tính giá trị của a và b trong G và H:
$$G^2 = \frac{1}{a+b} \Rightarrow a+b = \frac{1}{G^2}$$
$$H^2 = 4a - 4\sqrt{ab} + 4b = 4(\sqrt{a} - \sqrt{b})^2 \Rightarrow \sqrt{a} - \sqrt{b} = \frac{H}{2}$$
Từ đó, suy ra được:
$$\sqrt{a} + \sqrt{b} = \frac{1}{G}\sqrt{\frac{1}{G^2} + 4}$$
$$\Rightarrow 2\sqrt{a} = \frac{1}{G}\sqrt{\frac{1}{G^2} + 4} + H$$
$$\Rightarrow a = \left(\frac{1}{G}\sqrt{\frac{1}{G^2} + 4} + H\right)^2/4$$
$$\Rightarrow b = \left(\frac{1}{G}\sqrt{\frac{1}{G^2} + 4} - H\right)^2/4$$

Tiếp theo, ta tính giá trị của F:
$$F = 6\sqrt{3} + \sqrt{2} = 6\sqrt{3} + \sqrt{2}\frac{\sqrt{6}+\sqrt{2}}{2} = 6\sqrt{3} + 3\sqrt{2} + 3\sqrt{6}$$

Cuối cùng, ta tính giá trị của K:
$$K = 2xy\left(2\sqrt{x} + 3\sqrt{y}\right) = 2\sqrt{xy}(4\sqrt{x} + 6\sqrt{y})$$

Vậy, ta đã tính được giá trị của F, G, H và K.

a, căn a trừ b/ a-b^2

b, 2 căn a + 2 căn b /a-b

c, 6 căn a trừ 6 / 4a-1

a) căn a-b/a-b^2

b) 2(căn a+căn b)/a-b

c) 3(2 căn a-1)/4a-1

d)2xy(2 căn x-3 căn y)/4x-9y

a) √a -b /a-b²

b) 2√a+2b / a-b²

c) 6√a -3 / 4a-1

d) 4xy√x -6xy√y / 4x-9y

ý a liên hợp ms...ý b nhân mẫu số với \(\sqrt{2}\)

1) Ta có: \(3\sqrt{12}+\dfrac{1}{2}\sqrt{48}-\sqrt{27}\)

\(=3\cdot2\sqrt{3}+\dfrac{1}{2}\cdot4\sqrt{3}-3\sqrt{3}\)

\(=6\sqrt{3}+2\sqrt{3}-3\sqrt{3}\)

\(=5\sqrt{3}\)

2) Ta có: \(\dfrac{2}{\sqrt{3}-5}\)

\(=\dfrac{2\left(\sqrt{3}+5\right)}{\left(\sqrt{3}-5\right)\left(\sqrt{3}+5\right)}\)

\(=\dfrac{2\left(\sqrt{3}+5\right)}{3-25}\)

\(=\dfrac{-2\left(\sqrt{3}+5\right)}{22}\)

\(=\dfrac{-\sqrt{3}-5}{11}\)

3) Ta có: \(\sqrt{\dfrac{2}{5}}\)

\(=\dfrac{\sqrt{2}}{\sqrt{5}}\)

\(=\dfrac{\sqrt{2}\cdot\sqrt{5}}{5}\)

\(=\dfrac{\sqrt{10}}{5}\)

Bài 1:
a.

\(\frac{1}{2\sqrt{2}-3\sqrt{3}}=\frac{2\sqrt{2}+3\sqrt{3}}{(2\sqrt{2}-3\sqrt{3})(2\sqrt{2}+3\sqrt{3})}=\frac{2\sqrt{2}+3\sqrt{3}}{(2\sqrt{2})^2-(3\sqrt{3})^2}=\frac{2\sqrt{2}+3\sqrt{3}}{-19}\)

b.

\(=\sqrt{\frac{(3-\sqrt{5})^2}{(3-\sqrt{5})(3+\sqrt{5})}}=\sqrt{\frac{(3-\sqrt{5})^2}{3^2-5}}=\sqrt{\frac{(3-\sqrt{5})^2}{4}}=\sqrt{(\frac{3-\sqrt{5}}{2})^2}=|\frac{3-\sqrt{5}}{2}|=\frac{3-\sqrt{5}}{2}\)

Bài 2.

a. 

\(=\frac{\sqrt{8}(\sqrt{5}+\sqrt{3})}{(\sqrt{5}-\sqrt{3})(\sqrt{5}+\sqrt{3})}=\frac{2\sqrt{2}(\sqrt{5}+\sqrt{3})}{5-3}=\sqrt{2}(\sqrt{5}+\sqrt{3})=\sqrt{10}+\sqrt{6}\)

b.

\(=\sqrt{\frac{(2-\sqrt{3})^2}{(2-\sqrt{3})(2+\sqrt{3})}}=\sqrt{\frac{(2-\sqrt{3})^2}{2^2-3}}=\sqrt{(2-\sqrt{3})^2}=|2-\sqrt{3}|=2-\sqrt{3}\)

Bài 3:

a.

\(M=\left[\frac{15(\sqrt{6}-1)}{(\sqrt{6}+1)(\sqrt{6}-1)}+\frac{4(\sqrt{6}+2)}{(\sqrt{6}-2)(\sqrt{6}+2)}-\frac{12(3+\sqrt{6})}{(3-\sqrt{6})(3+\sqrt{6})}\right](\sqrt{6}+11)\)

\(=\left[\frac{15(\sqrt{6}-1)}{6-1}+\frac{4(\sqrt{6}+2)}{6-2^2}-\frac{12(3+\sqrt{6})}{3^2-6}\right](\sqrt{6}+11)\)

\(=[3(\sqrt{6}-1)+2(\sqrt{6}+2)-4(3+\sqrt{6})](\sqrt{6}+11)=(\sqrt{6}-11)(\sqrt{6}+11)=6-11^2=-115\)

b.

\(N=\left[1-\frac{\sqrt{5}(\sqrt{5}+1)}{\sqrt{5}+1}\right].\left[\frac{\sqrt{5}(\sqrt{5}-1)}{1-\sqrt{5}}-1\right]\)

\(=(1-\sqrt{5})(-\sqrt{5}-1)=(\sqrt{5}-1)(\sqrt{5}+1)=5-1=4\)

\(\dfrac{2ab}{\sqrt{a}-\sqrt{b}}=\dfrac{2ab\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}=\dfrac{2ab\left(\sqrt{a}+\sqrt{b}\right)}{a-b}\)

\(\dfrac{1}{\sqrt{x}-\sqrt{y}}=\dfrac{\sqrt{x}+\sqrt{y}}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}=\dfrac{\sqrt{x}+\sqrt{y}}{x-y}\)

\(\dfrac{3}{\sqrt{10}+\sqrt{7}}=\dfrac{3\left(\sqrt{10}-\sqrt{7}\right)}{\left(\sqrt{10}+\sqrt{7}\right)\left(\sqrt{10}-\sqrt{7}\right)}=\dfrac{3\left(\sqrt{10}-\sqrt{7}\right)}{10-7}=\dfrac{3\left(\sqrt{10}-\sqrt{7}\right)}{3}=\sqrt{10}-\sqrt{7}\)

\(\dfrac{2}{\sqrt{6}-\sqrt{5}}=\dfrac{2\left(\sqrt{6}+\sqrt{5}\right)}{\left(\sqrt{6}-\sqrt{5}\right)\left(\sqrt{6}+\sqrt{5}\right)}=\dfrac{2\left(\sqrt{6}+\sqrt{5}\right)}{6-5}=2\left(\sqrt{6}+\sqrt{5}\right)\)

ĐS:

a) \(\dfrac{\sqrt{2}}{1+\sqrt{2}-\sqrt{3}}=\dfrac{\sqrt{2}\left(1+\sqrt{2}+\sqrt{3}\right)}{\left(1+\sqrt{2}-\sqrt{3}\right)\left(1+\sqrt{2}+\sqrt{3}\right)}\dfrac{\sqrt{2}+2+\sqrt{6}}{\left(1+\sqrt{2}\right)^2-3}=\dfrac{\sqrt{2}+2+\sqrt{6}}{2\sqrt{2}+3-3}=\dfrac{\sqrt{2}+2+\sqrt{6}}{2\sqrt{2}}=\dfrac{1+\sqrt{2}+\sqrt{3}}{2}\)

b) \(\dfrac{1}{\sqrt{3}+\sqrt{2}-\sqrt{5}}=\dfrac{\sqrt{3}+\sqrt{2}+\sqrt{5}}{\left(\sqrt{3}+\sqrt{2}-\sqrt{5}\right)\left(\sqrt{3}+\sqrt{2}+\sqrt{5}\right)}=\dfrac{\sqrt{3}+\sqrt{2}+\sqrt{5}}{\left(\sqrt{3}+\sqrt{2}\right)^2-5}=\dfrac{\sqrt{3}+\sqrt{2}+\sqrt{5}}{2\sqrt{6}+5-5}=\dfrac{\sqrt{3}+\sqrt{2}+\sqrt{5}}{2\sqrt{6}}=\dfrac{3\sqrt{2}+2\sqrt{3}+\sqrt{30}}{2\sqrt{6}\cdot\sqrt{6}}=\dfrac{3\sqrt{2}+2\sqrt{3}+\sqrt{30}}{12}\)

\(\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)

\(\dfrac{2+\sqrt{3}}{2-\sqrt{3}}=\left(2+\sqrt{3}\right)^2=7+4\sqrt{3}\)