Cho một hình thang ABCD với hai đáy AB và CD gọi M,N là trung điểm của hai đáy
Chứng minh nếu MN vuông góc với hai đáy thì ABCD là hình thang cân ?
Những câu hỏi liên quan
Cho hình thang cân ABCD (AB//CD) có E và F lần lượt là trung điểm của hai đáy AB và CD. Chứng minh EF vuông góc với AB
Xét ΔADF và ΔBCF có
AD=BC
\(\widehat{D}=\widehat{C}\)
FD=FC
Do đó: ΔADF=ΔBCF
Suy ra: FA=FB
Xét ΔFAB có FA=FB
nên ΔFAB cân tại F
mà FE là đường trung tuyến ứng với cạnh đáy AB
nên FE là đường cao ứng với cạnh AB
hay FE\(\perp\)AB
Đúng 1
Bình luận (0)
Cho hình thang cân ABCD (AB//CD) có E và F lần lượt là trung điểm hai đáy AB và CD. Chứng minh EF vuông góc với AB
Gọi O là giao điểm của AC và BD.
Chứng minh: OE ^ AB.
Tương tự, có OF ^ CD.
Suy ra OF ^ AB. Vậy EF ^ AB
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AB BC CD a, AD 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy. Gọi M, N lần lượt là trung điểm của SB và CD. Tính cosin góc giữa MN và (SAC), biết thể tích khối chóp S.ABCD bằng
a
3
3
4
A
.
5
10
B...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AB = BC = CD = a, AD = 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy. Gọi M, N lần lượt là trung điểm của SB và CD. Tính cosin góc giữa MN và (SAC), biết thể tích khối chóp S.ABCD bằng a 3 3 4
A . 5 10
B . 3 310 20
C . 310 20
D . 3 5 10
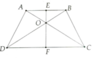
Cho hình thang ABCD, có đáy lớn là AB và đáy nhỏ là CD. Hai đường chéo AC
và BD vuông góc với nhau tại O. Trên các tia OA và OB tương ứng lấy hai điểm M và N sao
cho góc ANC =góc BMD = 90 độ. Gọi P là trung điểm của AB. Chứng minh rằng:
1. OA.OM =OB.ON.
2. Hai tam giác OMN,OBA đồng dạng và OP vuông góc MN.
Bài 1. Cho hình thang ABCD có đáy AB đáy CD và hai đường chéo AC và BD vuông góc. Trên đáy AB lấy M sao cho AM có độ dài bằng đường trung bình của hình thang ABCD. Chứng minh : CA là đường phân giác góc MCD .Bài 2: Cho tam giác ABC gọi M là trung điểm của của cạnh AB, kẻ đường phân giác trong BE của góc ABC. Dựng AI vuông góc với BE, cắt BC tại D a)Tam giác ABD là tam giác gì? c/m b)C/m: MI // BC c)Gọi N là giao điểm của MI và AC. C/m: AN NC Giúp em với ạ,em cảm ơn ạ
Đọc tiếp
Bài 1. Cho hình thang ABCD có đáy AB > đáy CD và hai đường chéo AC và BD vuông góc. Trên đáy AB lấy M sao cho AM có độ dài bằng đường trung bình của hình thang ABCD. Chứng minh : CA là đường phân giác góc MCD .
Bài 2: Cho tam giác ABC gọi M là trung điểm của của cạnh AB, kẻ đường phân giác trong BE của góc ABC. Dựng AI vuông góc với BE, cắt BC tại D
a)Tam giác ABD là tam giác gì? c/m
b)C/m: MI // BC
c)Gọi N là giao điểm của MI và AC. C/m: AN = NC
Giúp em với ạ,em cảm ơn ạ
Cho hình thang cân ABCD, hai đáy AB,CD. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh :
a) Tam giác ANB cân.
b) MN là trung trực của đoạn thẳng AB.
a)Xét ΔADN và ΔBCN có: AD=BC; góc D= góc C (ABCD là hình thang cân); DN=CN( N là trung điểm của CD). Vậy ΔADN= ΔBCN (c.g.c)→AN=BN→Tam giác ANB cân
b) Vì ΔANB cân, có NM là đường trung tuyến nên đồng thời cũng là đường trung trực của đoạn thẳng AB
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD đáy ABCD là hình thang cân,
A
D
a
,
A
B
a
,
B
C
a
,
C
D
2
a
.
Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Gọi M, N lần lượt là trung điểm của SB và SD. Tính cosin góc giữa MN và (SAC) biết thể tích khối chóp S.ABCD bằng
a...
Đọc tiếp
Cho hình chóp S.ABCD đáy ABCD là hình thang cân, A D = a , A B = a , B C = a , C D = 2 a . Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Gọi M, N lần lượt là trung điểm của SB và SD. Tính cosin góc giữa MN và (SAC) biết thể tích khối chóp S.ABCD bằng a 3 3 4
A. 310 20
B. 3 5 10
C. 3 310 20
D. 5 10
Cho hình thang cân ABCD có hai đáy AB// CD. Gọi I là giao điểm của 2 đường chéo AC và BD . Đường trung trực của AD và DI cắt nhau tại O. Chứng minh rằng OI vuông góc với BC.
#hinh_thang_can_ABCD
Cho hình thang ABCD, có đáy AB//CD, AB>CD và hai đường chéo AC và BD vuông góc với nhau. Trên cạnh đáy AB lấy điểm M sao cho AM có độ dài bằng độ dài đường trung bình của hình thang. Chứng minh CA là đường phân giác của góc MCD.