tính tích đơn thức sau rồi tìm bậc, hệ số của tích vừa tìm được:
1/4xy^3 và -2x^2yz^2 .
tính tích 2 đơn thức
\(-0,5x^2yz\) và \(-3xy^3z\)
Tìm hệ số và bậc của tích vừa tìm được
`@` `\text {Ans}`
`\downarrow`
`-0,5x^2yz*(-3xy^3z)`
`= [(-0,5)*(-3)]*(x^2*x)*(y*y^3)*(z*z)`
`= 1,5x^3y^4z^2`
Hệ số: `1,5`
Bậc: `3+4+2 = 9`
`@` `\text {Kaizuu lv u}`
Tính tích các đơn thức sau rồi tìm hệ số và bậc của tích tìm được
a) \(\dfrac{1}{4}xy^3\) và \(-2x^2yz^2\)
b) \(-2x^2yz\) và \(-3xy^3z\)
a) Tích của và là:
Đơn thức tích có hệ số là ; có bậc 9.
b) Tích của và là:
Đơn thức có hệ số là 6; có bậc 9.
a) \(\dfrac{1}{4}xy^3.\left(-2\right)x^2yz^2\)
= \(\left[\dfrac{1}{4}.\left(-2\right)\right].\left(x.x^2\right).\left(y^3.y\right).z^2\)
= \(\dfrac{-1}{2}x^3y^4z^2\).
Đơn thức trên có hệ số là \(\dfrac{-1}{2}\) và bậc là 9.
b) \(-2x^2yz.\left(-3\right)xy^3z\)
= \(\left[\left(-2\right).\left(-3\right)\right].\left(x^2.x\right).\left(y.y^3\right).\left(z.z\right)\)
= 6x\(^3y^4z^2\).
Đơn thức trên có hệ số là 6 và bậc là 9.
a) Ta có: 1/4xy³.(-2x²yz²) = 1/2(-2)xy³.x²yz² = -1/2x³y4z²
– Hệ số của tích là -1/2 và tích có bậc là 9.
b)Ta có: 2x²yz.(-3xy³z) = -(2).(-3)x²yz.xy³z = 6x³y4z²
Hệ số của tích là 6 và tích có bậc là 9.
a) 6xy.2x3yz2=(6.2).(x.x3).(y.y).z2=12x4.y2.z2
=> Hệ số: 12; Phần biến: x4y2z2; Bậc đơn thức: 8
b) 12x3y2.(-3/4 xy2)= [12.(-3/4)]. (x3.x).(y2.y2)= -9.x4.y4
=> Hệ số: -9; Phần biến: x4.y4; Bậc đơn thức: 8
c)
\(\dfrac{1}{5}x^3y.\left(-5x^4yz^3\right)=\left[\dfrac{1}{5}.\left(-5\right)\right].\left(x^3.x^4\right).\left(y.y\right).z^3\\ =-x^7y^2z^3\)
=> Hệ số: -1; Phần biến: x7y2z3; Bậc đơn thức: 12
d) \(-\dfrac{3}{8}x^3y^2z.\left(4x^2yz\right)^3=\left[-\dfrac{3}{8}.4^2\right].\left(x^3.x^{2.3}\right).\left(y^2.y\right).\left(z.z^3\right)=-6.x^9y^3z^4\)
=> Hệ số: -6; Phần biến: x9y3z4; Bậc đơn thức: 16
a) Ta có: \(6xy\cdot2x^3yz^2\)
\(=\left(6\cdot2\right)\cdot\left(x\cdot x^3\right)\cdot\left(y\cdot y\right)\cdot z^2\)
\(=12x^4y^2z^2\)
Hệ số là 12
Phần biến là \(x^4;y^2;z^2\)
Bậc là 8
b) Ta có: \(12x^3y^2\cdot\left(-\dfrac{3}{4}xy^2\right)\)
\(=\left[12\cdot\left(-\dfrac{3}{4}\right)\right]\cdot\left(x^3\cdot x\right)\cdot\left(y^2\cdot y^2\right)\)
\(=-9x^4y^4\)
Hệ số là 9
Phần biến là \(x^4;y^4\)
Bậc là 8
tính tích rồi tìm bậc cúa chúng
1/4xy^3 và -2x^2yz^2
\(=-\dfrac{1}{4}\cdot2\cdot xy^3\cdot xyz^2=-\dfrac{1}{2}x^2y^4z^2\)
Bậc là 8
tính tích hai đơn thức 1/4 xy3 và -2x2yz2
tìm hệ số và bậc của tích vừa tìm được ?
1 Tìm tích của các đơn thức sau rồi tìm bậc của đơn thức thu được
a,2x^2y^3 và -5x^3y^4
b,1/4x^3yz và -2x^3y^5
c,4xy^2 và -3/4x^3y^2
\(2x^2y^3\)và \(-5x^3y^4\)
-10x5x7
b, \(\frac{1}{2}x^6y^6z\)
c,Tự lm tương tự
k nhá
Tính giá trị biểu thức: \(2x^2-5x+2\) tại x=-1 và tại x=\(\dfrac{1}{2}\)
Tính tích của các đơn thức sau rồi xác định hệ số và bậc của tích tìm được
\(\dfrac{1}{2}xy^2\) ; -3xyz ; 2x2z
1.
Tại x = -1, có :
2.(-1)2 - 5.(-1) + 2
= 2.1 + 5 + 2
= 9
Tại x = \(\dfrac{1}{2}\), có :
\(2.\left(\dfrac{1}{2}\right)^2-5.\dfrac{1}{2}+2\)
= \(2.\dfrac{1}{4}-2,5+2\)
= 0,5 - 2,5 + 2
= 0
2.
\(\dfrac{1}{2}xy^2.\left(-3xyz\right).2x^2z\)
= -3x4y3z2
- Hệ số : -3
- Bậc : 9
thay x =-1 vào bt ta được
\(2\left(-1\right)^2-5\left(-1\right)+2=2+5+2=9\)
thay x=1/2 vào bt ta được
\(2.\left(\dfrac{1}{2}\right)^2-5.\dfrac{1}{2}+2=\dfrac{1}{2}-\dfrac{5}{2}+\dfrac{4}{2}=0\)
\(\dfrac{1}{2}xy^2.-3xyz.2x^2z=-3x^4y^3z\)2
hệ số là -3 bậc 9
Tính tích của các đơn thức sau rồi tìm hệ số và bậc của tích tìm được.
1 4 x y 3 v à 2 x 2 y z 2
Ta có
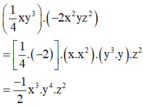
Đơn thức trên có hệ số bằng -1/2.
Bậc của tích trên là tổng bậc của các biến :
Biến x có bậc 3
Biến y có bậc 4
Biến z có bậc 2
⇒ Tích có bậc : 3 + 4 + 2 = 9.
Tính tích của các đơn thức sau rồi tìm hệ số và bậc của tích tìm được.
- 2 x 2 y z v à - 3 x y 3 z
(-2x2yz).(-3xy3z) = [(-2).(-3)].(x2.x)(y.y3).(z.z) = 6.x3.y4.z2
Đơn thức trên có hệ số bằng 6.
Bậc của tích trên là tổng bậc của các biến :
Biến x có bậc 3
Biến y có bậc 4
Biến z có bậc 2
⇒ Tích có bậc : 3 + 4 + 2 = 9