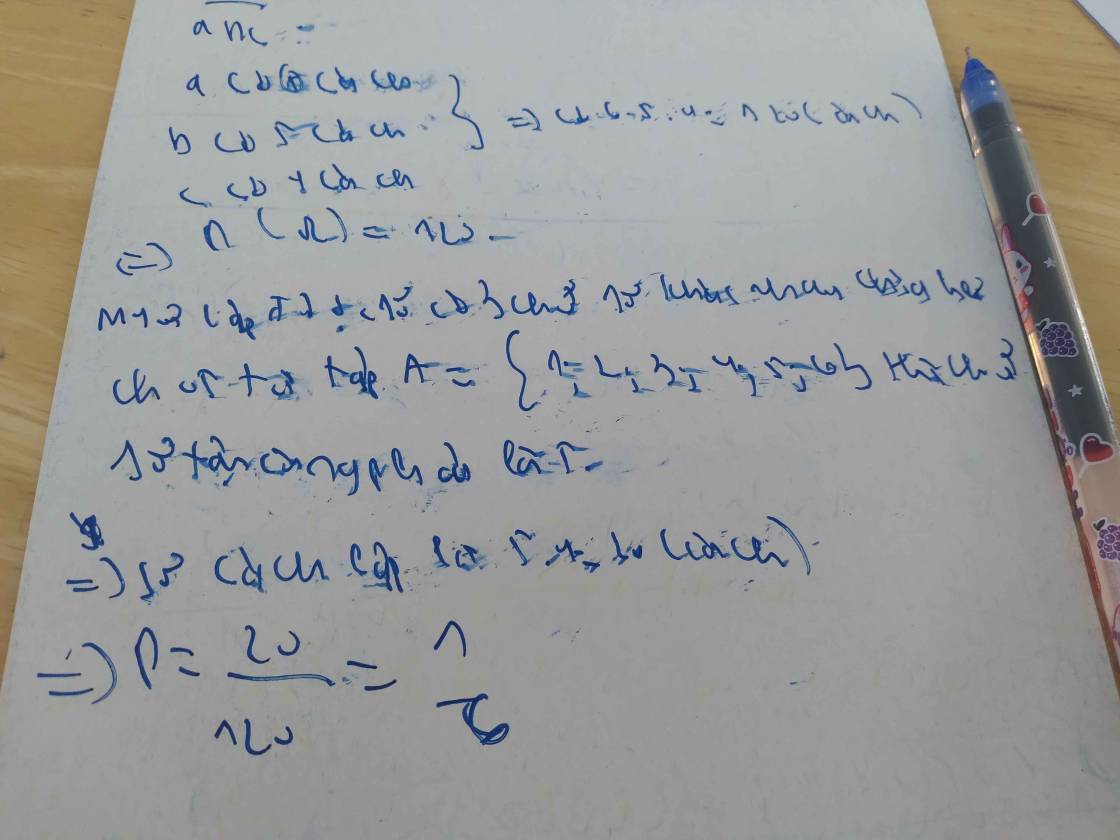Chọn ngẫu nhiên một số có 3 chữ số được lập từ các chữ số 0;1;2;3;4;5. Tính xác suất để số chọn được chia hết cho 3

Những câu hỏi liên quan
Tập S gồm các số tự nhiên có 6 chữ số khác nhau được thành lập từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8. Chọn ngẫu nhiên một số từ tập S. Xác suất để số được chọn không có hai chữ số chẵn đứng cạnh nhau là: A.
11
70
B.
29
140
C.
13
80
D.
97
560
Đọc tiếp
Tập S gồm các số tự nhiên có 6 chữ số khác nhau được thành lập từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8. Chọn ngẫu nhiên một số từ tập S. Xác suất để số được chọn không có hai chữ số chẵn đứng cạnh nhau là:
A. 11 70
B. 29 140
C. 13 80
D. 97 560
Gọi S là tập hợp các số tự nhiên có ba chữ số (không nhất thiết khác nhau) được lập từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9. Chọn ngẫu nhiên một số từ S. Tính xác suất để số được chọn thỏa mãn a≤b≤c A.
1
6
B.
11
60
C.
13
60
D.
9
11
Đọc tiếp
Gọi S là tập hợp các số tự nhiên có ba chữ số (không nhất thiết khác nhau) được lập từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9. Chọn ngẫu nhiên một số từ S. Tính xác suất để số được chọn thỏa mãn a≤b≤c
A. 1 6
B. 11 60
C. 13 60
D. 9 11
Chọn đáp án B
Phương pháp
Chia các TH sau:
TH1: a<b<c.
TH2: a=b<c.
TH3: a<b=c.
TH4: a=b=c.
Cách giải
Gọi số tự nhiên có 3 chữ số là a b c ¯ (0≤a,b,c≤9, a≠0).
=> S có 9.10.10=900 phần tử. Chọn ngẫu nhiên một số từ S => n(Ω)=900
Gọi A là biến cố: “Số được chọn thỏa mãn a≤b≤c”.
TH1: a<b<c. Chọn 3 số trong 9 số từ 1 đến 9, có duy nhất một cách xếp chúng theo thứ tự tăng dần từ trái qua phải nên TH này có C 9 3 số thỏa mãn.
TH2: a=b<c, có C 9 2 số thỏa mãn.
TH3: a<b=c có C 9 2 số thỏa mãn.
TH4: a=b=c có 9 số thỏa mãn.
⇒ n ( A ) = C 9 3 + 2 C 9 2 + 9 = 165
Vậy P ( A ) = 11 60 .
Đúng 0
Bình luận (0)
Gọi S là tập hợp các số tự nhiên có ba chữ số (không nhất thiết khác nhau) được lập từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9. Chọn ngẫu nhiên một số
a
b
c
¯
từ S. Tính xác suất để số được chọn thỏa mãn
a
≤
b
≤
c
.
Đọc tiếp
Gọi S là tập hợp các số tự nhiên có ba chữ số (không nhất thiết khác nhau) được lập từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9. Chọn ngẫu nhiên một số a b c ¯ từ S. Tính xác suất để số được chọn thỏa mãn a ≤ b ≤ c .
![]()
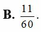
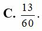
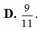
gọi s là tập hợp tất cả các số tự nhiên có 3 chữ số đôi một khác nhau được lập từ các chữ số 1,2,3,4,5,6. Chọn ngẫu nhiên một số từ S, tính xác suất để số được chọn là 1 số chia hết cho 5
Không gian mẫu: \(A_6^3=120\)
Gọi số cần lập có dạng \(\overline{abc}\)
Số chia hết cho 5 \(\Rightarrow c=5\) (1 cách chọn)
Chọn và hoán vị cặp ab: \(A_5^2=20\) cách
\(\Rightarrow1.20=20\) số chia hết cho 5
Xác suất: \(P=\dfrac{20}{120}=\dfrac{1}{6}\)
Đúng 1
Bình luận (1)
Gọi S là tập hợp tất cả các số tự nhiên có 3 chữ số đôi một khác nhau được lập từ các chữ số 0,1,2,3,4,5,6. Chọn ngẫu nhiên một số từ tập S. Tính xác suất để số được chọn là một số chia hết cho 6
Gọi S là tập hợp các số tự nhiên có 5 chữ số đôi một khác nhau được lập từ các chữ số 0,1,2,3,4,5,6,7. Chọn ngẫu nhiên một số thuộc S. Tính xác suất sao cho số được chọn có đúng 3 chữ số chẵn và 2 chữ số lẻ, đồng thời 2 chữ số lẻ đứng liền nhau.
Không gian mẫu: \(n_{\Omega}=A_8^5-A_7^4=5880\)
Chọn 3 chữ số chẵn: \(C_4^3=4\) cách
Chọn 2 chữ số lẻ: \(C_4^2=6\) cách
Xếp 2 số lẻ liền nhau, sau đó hoán vị với 3 chữ số chẵn: \(2!.4!=48\) cách
Chọn 3 chữ số chẵn sao cho có mặt chữ số 0: \(C_3^2=3\) cách
Hoán vị 5 chữ số sao cho 2 số lẻ liền nhau và số 0 đứng đầu: \(2!.3!=12\) cách
\(\Rightarrow6.\left(4.48-3.12\right)=936\)
Xác suất: \(P=\dfrac{936}{5880}=\dfrac{39}{245}\)
Đúng 0
Bình luận (2)
Gọi A là tập các số tự nhiên có 6 chữ số đôi một khác nhau được tạo ra từ các chữ số 0, 1, 2, 3, 4, 5. Từ A chọn ngẫu nhiên một số. Tính xác suất để số được chọn có chữ số 3 và chữ số 4 đứng cạnh nhau A.
4
25
.
B.
4
15
.
C.
8
25
.
D.
2
15
.
Đọc tiếp
Gọi A là tập các số tự nhiên có 6 chữ số đôi một khác nhau được tạo ra từ các chữ số 0, 1, 2, 3, 4, 5. Từ A chọn ngẫu nhiên một số. Tính xác suất để số được chọn có chữ số 3 và chữ số 4 đứng cạnh nhau
A. 4 25 .
B. 4 15 .
C. 8 25 .
D. 2 15 .
Gọi A là tập các số tự nhiên có 6 chữ số đôi một khác nhau được tạo ra từ các chữ số 0, 1, 2, 3, 4, 5. Từ A chọn ngẫu nhiên một số. Tính xác suất để số được chọn có chữ số 3 và chữ số 4 đứng cạnh nhau.
Đọc tiếp
Gọi A là tập các số tự nhiên có 6 chữ số đôi một khác nhau được tạo ra từ các chữ số 0, 1, 2, 3, 4, 5. Từ A chọn ngẫu nhiên một số. Tính xác suất để số được chọn có chữ số 3 và chữ số 4 đứng cạnh nhau.
![]()
![]()
![]()
![]()
Đáp án C.
Số cách lập số có 5 chữ số có 3 và 4 đứng cạnh nhau là 2(4.4.3.2) = 192 cách.
Số cách lập số có 6 chứ số đôi một khác nhau từ A là 5.5.4.3.2=600 cách
Suy ra xác suất cần tìm là 192 600 = 8 25
Đúng 0
Bình luận (0)
Gọi E là tập hợp các số tự nhiên có 3 chữ số đôi một khác nhau lập được từ các chữ số 1, 2, 3, 4, 7. Chọn ngẫu nhiên một phần tử của E. Tính xác suất để số được chọn chia hết cho 3 A.
1
5
B.
2
5
C.
3
5
D.
4
5
Đọc tiếp
Gọi E là tập hợp các số tự nhiên có 3 chữ số đôi một khác nhau lập được từ các chữ số 1, 2, 3, 4, 7. Chọn ngẫu nhiên một phần tử của E. Tính xác suất để số được chọn chia hết cho 3
A. 1 5
B. 2 5
C. 3 5
D. 4 5