Bài 5: Cho ΔABC cân tại A có AB = AC = 6cm; BC = 4cm. Các đường phân giác BD và CE cắt nhau tại I (E trên AB và D trên AC)
a. Tính độ dài AD, ED.
b. Cm ΔADB đồng dạng với ΔAEC
c. Cm IE.CD = ID.BE
d. Cho SABC = 60 cm². Tính SAED.
Cho ΔABC cân tại A có AB=AC=6cm, BC=4cm. Tính bán kính đường tròn tìm ngoại tiếp ΔABC
Gọi O là tâm đường tròn ngoại tiếp ΔABC
Gọi H là giao của AO với BC
AB=AC
OB=OC
Do đó: AO là trung trực của BC
=>AH là trung trực của BC
=>H là trung điểm của BC
HB=HC=4/2=2cm
Kẻ giao của AO với (O) là D
=>AD là đường kính của (O)
Xét (O) có
ΔABD nội tiếp
ADlà đường kính
Do đó: ΔBAD vuông tại B
ΔAHB vuông tại H
=>AH^2+HB^2=AB^2
=>\(AH^2=6^2-2^2=32\)
=>\(AH=4\sqrt{2}\left(cm\right)\)
Xét ΔBAD vuông tại B có BH là đường cao
nên AB^2=AH*AD
=>\(AD=\dfrac{6^2}{4\sqrt{2}}=\dfrac{9}{\sqrt{2}}\left(cm\right)\)
=>\(R=\dfrac{AD}{2}=\dfrac{9}{2\sqrt{2}}\left(cm\right)\)
Bài 5. Cho ΔABC vuông tại A (AB < AC), tia phân giác của ![]() cắt AC tại D. Vẽ
cắt AC tại D. Vẽ ![]() tại E.
tại E.
a) Cho AB = 6cm, AC = 8cm. Tính BC.
b) Chứng minh ΔABD = ΔEBD.
c) So sánh AD và DC.
d) Gọi I là giao điểm của tia ED và BA. Chứng minh ΔDIC cân.
a: BC=căn 6^2+8^2=10cm
b: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
c: DA=DE
DE<DC
=>DA<DC
d: Xét ΔDAI vuông tại A và ΔDEC vuông tại E có
DA=DE
góc ADI=góc EDC
=>ΔDAI=ΔDEC
=>DI=DC
=>ΔDIC cân tại D
Bài 2: Cho ΔABC ⊥ tại A, đường cao AH, đường phân giác AD, kẻ DA⊥AC (K∈AC)
a) Cm ΔABC đồng dạng ΔHAC
b) Cho AB= 6cm, AC= 8cm. Tính BD
c) Cm AC.AD=√2AB.CK
Giúp mk vs ;-;
a) Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{C}\) chung
Do đó: ΔABC\(\sim\)ΔHAC(g-g)
b) Áp dụng định lí Pytago vào ΔACB vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{BD}{6}=\dfrac{CD}{8}\)
mà BD+CD=BC=10cm(D nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{6}=\dfrac{CD}{8}=\dfrac{BD+CD}{6+8}=\dfrac{10}{14}=\dfrac{5}{7}\)
Do đó: \(\dfrac{BD}{6}=\dfrac{5}{7}\)
hay \(BD=\dfrac{30}{7}cm\)
Vậy: \(BD=\dfrac{30}{7}cm\)
bài 11 ΔABC có góc BAC = ,AB=6cm,AC=12 cm ,phân giác góc BAC cắt BC tại D.Tính AD?
bài 12 cho tam giác ABC có góc A =, AB=3cm,AC=6cm.Tính độ dài đường phân giác AD?
11:
\(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos60=\dfrac{2\cdot6\cdot12}{6+12}\cdot\dfrac{1}{2}=4\left(cm\right)\)
12:
\(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos60=\dfrac{2\cdot3\cdot6}{3+6}\cdot\dfrac{1}{2}=\dfrac{3\cdot6}{3+6}=\dfrac{18}{9}=2\left(cm\right)\)
Cho ΔABC cân tại A. Vẽ phân giác BD,CE.
a) Chứng minh: BD=CE
b) Chứng minh DE=BC
c) Biết AB=AC=6cm, BC=4cm. Tính AD, DC
Cho tam giác ΔABC vuông tại A có AB=6cm,AC=10cm . Đường cao AH a)Chứng minh ΔABC / ΔABH b)Chứng minh AB²=BH.BC c)Tính BC,AH,BH
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: ta có: ΔABC\(\sim\)ΔHBA
nên BA/BH=BC/BA
hay \(BA^2=BH\cdot BC\)
a.Xét tam giác ABC và tam giác HBA, có:
^B: chung
^BAC = ^BHA = 90 độ
Vậy tam giác ABC đồng dạng tam giác HBA (g.g)
b.\(\rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\)
\(\Leftrightarrow AB^2=BH.BC\left(đfcm\right)\) (1)
c.Áp dụng định lý pitago \(\Rightarrow BC=\sqrt{6^2+10^2}=2\sqrt{34}\left(cm\right)\)
(1) \(\Leftrightarrow6^2=2\sqrt{34}BH\)
\(\Leftrightarrow BH=\dfrac{9\sqrt{34}}{17}\left(cm\right)\)
Áp dụng định lý pitago trong tam giác ABH \(\Rightarrow AH=\sqrt{6^2-\left(\dfrac{9\sqrt{34}}{17}\right)^2}=\dfrac{15\sqrt{34}}{17}\left(cm\right)\)
cho ΔABC cân tại A , có AB = 5cm , BC= 6cm . Từ A kẻ AH⊥BC (HϵBC).
a . Tính AH
B. Gọi G là trọng tâm của ΔABC . Trên tia AG lấy điểm D sao cho AG = GD . Tia CG cắt AB tại F . CM BD = \(\dfrac{2}{3}\)CF
C. CM DB+DG>AB
Cho ΔABC vuông tại A, có AH vuông góc BC. Tính AB biết HB = 2cm; HC=8cm, AC=6cm
\(BC=BH+HC=2+8=10\left(cm\right)\)
△ABC vuông tại A có \(BC^2=AB^2+AC^2\\ \Rightarrow AB^2=BC^2-AC^2=10^2-6^2=64\\ \Rightarrow AB=8\left(cm\right)\)
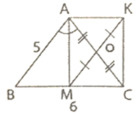
Bài 4: (3 điểm) Cho ΔABC cân tại A có AB = 5cm; BC = 6cm. Kẻ phân giác trong AM (M ∈ BC) . Gọi O là trung điểm của AC và K là điểm đối xứng của M qua O.
a) Tính diện tích tam giác ABC.
b) Tứ giác ABMO là hình gì? Vì sao?
c) Để tứ giác AMCK là hình vuông thì tam giác ABC phải có thêm điều kiện gì?
a) Vì \(\widehat{M}\) là trung điểm của \(\widehat{BC}\) nên:
\(\widehat{BM}=\dfrac{BC}{2}=\dfrac{6}{2}=3\left(cm\right)\)
\(\Delta ABC\) cân tại \(A\), lại có \(\widehat{AM}\) là đường phân giác nên \(\widehat{AM}\) cũng là đường cao. Do đó \(\Delta AMB\) vuông tại \(\widehat{M}\)
\(\Rightarrow AM^2=AB^2-BM^2\) ( theo định lí Pytago )
\(\Rightarrow\widehat{AM}=4cm\)
\(S_{ABC}=\dfrac{AM.BC}{2}=\dfrac{4.6}{2}=12\left(cm^2\right)\)
b) \(\Delta AMC\) vuông tại\(M\) có \(\widehat{MO}\) là đường trung tuyến nên \(\widehat{OM}=\widehat{OA}\)
\(\Rightarrow\text{∠}OAM=\text{∠}OMA\)( \(\Delta AMO\) cân tại \(O\))
Lại có \(\text{∠}OAM=\text{∠}MAB\) ( \(AM\) là tia phân giác của \(BAC\) )
\(\Rightarrow\text{∠}OMA=\text{∠}MAB\)
Mà đây là 2 góc ở vị trí so le trong
\(\Rightarrow OM\text{ // }AB\)
Vậy tứ giác \(ABMO\) là hình thang.
c) Tứ giác \(AMCK\) có \(\widehat{OA}=\widehat{OC};\widehat{OM}=\widehat{OK}\) nên tứ giác \(AMCK\) là hình bình hành . Lại có \(\text{∠}AMC=90^o\)(chứng minh trên) nên tứ giác \(ACMK\) là hình chữ nhật
Hình chữ nhật \(ACMK\) là hình vuông
\(\Leftrightarrow\widehat{AM}=\widehat{MC}=\widehat{BM}\)
\(\Leftrightarrow\widehat{AM}=\dfrac{BC}{2}\)
\(\Leftrightarrow\Delta ABC\) vuông tại \(\widehat{A}\)
TK
a) Vì M là trung điểm của BC nên:
BM = BC/2 = 6/2 = 3(cm)
Tam giác ABC cân tại A, lại có AM là đường phân giác nên AM cũng là đường cao. Do đó tam giác AMB vuông tại M.
Suy ra: AM2 = AB2 - BM2 (Định lí Pytago)
= 52 - 32 = 16(cm)
Suy ra AM = 4cm
b) ΔAMC vuông tại M có MO là đường trung tuyến nên OM = OA.
Suy ra ∠OAM = ∠OMA ( ΔAMO cân tại O)
Lại có ∠OAM = ∠MAB (AM là tia phân giác góc BAC)
Suy ra ∠OMA = ∠MAB
Mà đây là 2 góc ở vị trí so le trong
Suy ra OM // AB
Vậy tứ giác ABMO là hình thang.
c) Tứ giác AMCK có OA = OC; OM = OK nên tứ giác AMCK là hình bình hành . Lại có ∠AMC = 90o (chứng minh trên) nên tứ giác AMCK là hình chữ nhật.
Hình chữ nhật AMCK là hình vuông
⇔ AM = MC = BM
⇔ AM = BC/2
⇔ ΔABC vuông cân tại A.