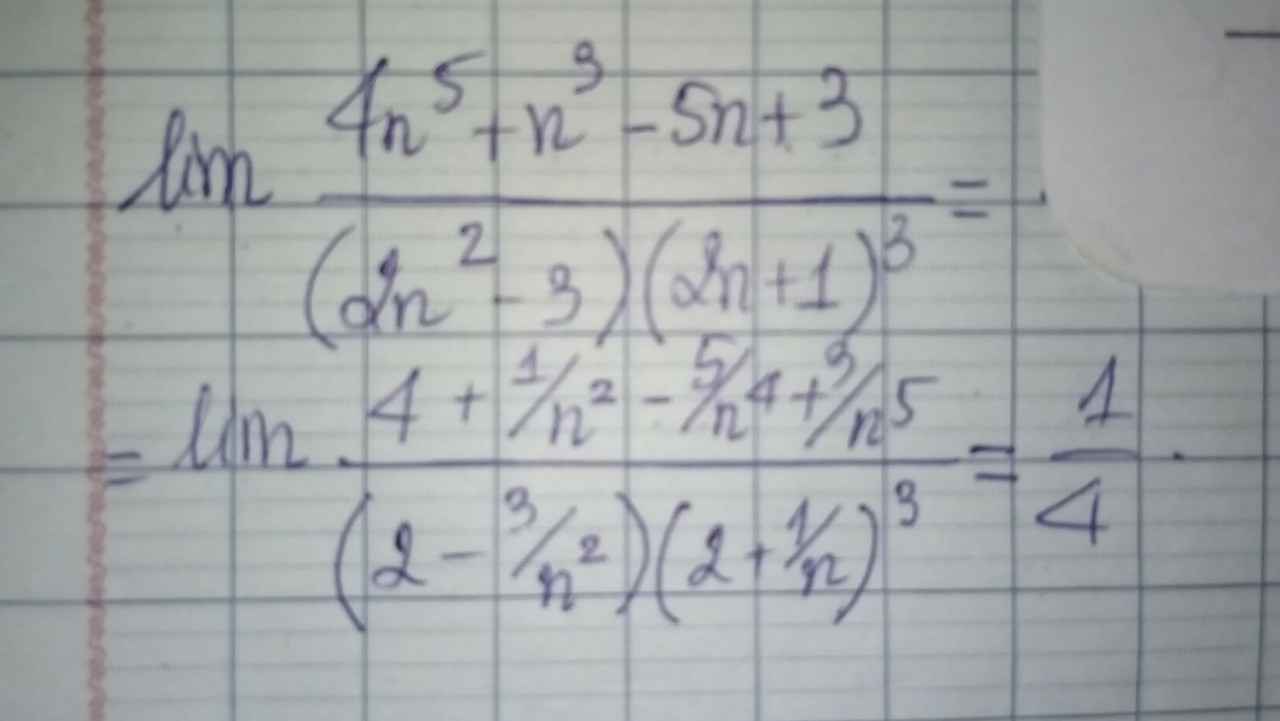giai phuong trinh \(\left(16x^{4n}+1\right)\left(y^{4n}+1\right)\left(z^{4n}+1\right)=32x^{2n}.y^{2n}.z^{2n}\)

Những câu hỏi liên quan
Cho \(f\left(n\right)=\dfrac{4n+\sqrt{4n^2-1}}{\sqrt{2n+1}+\sqrt[]{2n-1}}\) với n nguyên dương. Tính \(f\left(1\right)+f\left(2\right)+...+f\left(40\right)\).
\(f\left(n\right)=\dfrac{2n-1+2n+1+\sqrt{\left(2n+1\right)\left(2n+1\right)}}{\sqrt{2n+1}+\sqrt{2n-1}}\\ f\left(n\right)=\dfrac{\left(\sqrt{2n+1}-\sqrt{2n-1}\right)\left(2n-1+2n+1+\sqrt{\left(2n+1\right)\left(2n+1\right)}\right)}{2n+1-2n+1}\\ f\left(n\right)=\dfrac{\left(\sqrt{2n+1}\right)^3-\left(\sqrt{2n+1}\right)^3}{2}=\dfrac{\left(2n+1\right)\sqrt{2n+1}-\left(2n-1\right)\sqrt{2n+1}}{2}\)
\(\Leftrightarrow f\left(1\right)+f\left(2\right)+...+f\left(40\right)=\dfrac{3\sqrt{3}-1\sqrt{1}+5\sqrt{5}-3\sqrt{3}+...+81\sqrt{81}-79\sqrt{79}}{2}\\ =\dfrac{81\sqrt{81}-1\sqrt{1}}{2}=\dfrac{9^3-1}{2}=364\)
Đúng 1
Bình luận (0)
1, x,y,z∈N*. CMR x+3z-y là hợp số biết `x^2+y^2=z^2`
2,Tìm n∈N* để \(\left(4n^3+n+3\right)⋮\left(2n^2+n+1\right)\)
3, CMR:\(\dfrac{1}{\left(x-y\right)^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2}\ge\dfrac{4}{xy}\forall x\ne y,xy\ne0\)
2.
\(4n^3+n+3=4n^3+2n^2+2n-2n^2-n-1+4=2n\left(2n^2+n+1\right)-\left(2n^2+n+1\right)+4\)-Để \(\left(4n^3+n+3\right)⋮\left(2n^2+n+1\right)\) thì \(4⋮\left(2n^2+n+1\right)\)
\(\Leftrightarrow2n^2+n+1\in\left\{1;-1;2;-2;4;-4\right\}\) (do n là số nguyên)
*\(2n^2+n+1=1\Leftrightarrow n\left(2n+1\right)=0\Leftrightarrow n=0\) (loại) hay \(n=\dfrac{-1}{2}\) (loại)
*\(2n^2+n+1=-1\Leftrightarrow2n^2+n+2=0\) (phương trình vô nghiệm)
\(2n^2+n+1=2\Leftrightarrow2n^2+n-1=0\Leftrightarrow n^2+n+n^2-1=0\Leftrightarrow n\left(n+1\right)+\left(n+1\right)\left(n-1\right)=0\Leftrightarrow\left(n+1\right)\left(2n-1\right)=0\)
\(\Leftrightarrow n=-1\) (loại) hay \(n=\dfrac{1}{2}\) (loại)
\(2n^2+n+1=-2\Leftrightarrow2n^2+n+3=0\) (phương trình vô nghiệm)
\(2n^2+n+1=4\Leftrightarrow2n^2+n-3=0\Leftrightarrow2n^2-2n+3n-3=0\Leftrightarrow2n\left(n-1\right)+3\left(n-1\right)=0\Leftrightarrow\left(n-1\right)\left(2n+3\right)=0\)\(\Leftrightarrow n=1\left(nhận\right)\) hay \(n=\dfrac{-3}{2}\left(loại\right)\)
-Vậy \(n=1\)
Đúng 2
Bình luận (2)
1. \(x^2+y^2=z^2\)
\(\Rightarrow x^2+y^2-z^2=0\)
\(\Rightarrow\left(x-z\right)\left(x+z\right)+y^2=0\)
-TH1: y lẻ \(\Rightarrow x-z;x+z\) đều lẻ.
\(x+3z-y=x+z-y+2x\) chia hết cho 2. \(\Rightarrow\)Hợp số.
-TH2: y chẵn \(\Rightarrow\)1 trong hai biểu thức \(x-z;x+z\) chia hết cho 2.
*Xét \(\left(x-z\right)⋮2\):
\(x+3z-y=x-z+4z-y\) chia hết cho 2. \(\Rightarrow\)Hợp số.
*Xét \(\left(x+z\right)⋮2\):
\(x+3z-y=x+z+2z-y\) chia hết cho 2 \(\Rightarrow\)Hợp số.
Đúng 2
Bình luận (0)
Tính giới hạn :
L = lim \(\dfrac{\left(n^2+2n\right)\left(2n^3+1\right)\left(4n+5\right)}{\left(n^4-3n-1\right)\left(3n^2-7\right)}\)
Dang này thì cứ chọn số hạng có mũ cao nhất trên tử và mẫu là được. Nó là ngắt vô cùng lớn hay bé gì đấy
\(=lim\dfrac{8n^6}{3n^6}=\dfrac{8}{3}\)
Đúng 1
Bình luận (0)
Đề:Cho m,n là các số nguyên dương với n1.Đặt Pm^2n^2-4m+4nChứng minh rằng nếu P là số chính phương thì mnGiả sử mn1 Xét left(mn^2-2right)^2-n^2left(m^2n^2-4m+4nright)m^2n^4-4mn^2+4-mn^4+4mn^2-4n^3-4n^3+4 0 với forall n1Rightarrowleft(mn^2-2right)^2 n^2left(m^2n^2-4n+4nright)left(1right)Xét n^2left(m^2n^2-4m+4nright)-m^2n^4m^2n^4-4mn^2+4n^3-m^2n^4-4mn^2+4n^3-4n^2left(m-nright) 0 với forall mn1Rightarrow n^2left(m^2n^2-4m+4nright) m^2n^4left(2right)Từ left(1right);left(2right)Rightarrowleft(mn^2-...
Đọc tiếp
Đề:Cho m,n là các số nguyên dương với \(n>1\).Đặt \(P=m^2n^2-4m+4n\)
Chứng minh rằng nếu P là số chính phương thì m=n
Giả sử \(m>n>1\)
Xét \(\left(mn^2-2\right)^2-n^2\left(m^2n^2-4m+4n\right)\)
\(=m^2n^4-4mn^2+4-mn^4+4mn^2-4n^3\)
\(=-4n^3+4< 0\) với \(\forall n>1\)
\(\Rightarrow\left(mn^2-2\right)^2< n^2\left(m^2n^2-4n+4n\right)\left(1\right)\)
Xét \(n^2\left(m^2n^2-4m+4n\right)-m^2n^4\)
\(=m^2n^4-4mn^2+4n^3-m^2n^4\)
\(=-4mn^2+4n^3\)
\(=-4n^2\left(m-n\right)< 0\) với \(\forall m>n>1\)
\(\Rightarrow n^2\left(m^2n^2-4m+4n\right)< m^2n^4\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\left(mn^2-2\right)^2< n^2\left(m^2n^2-4m+4n\right)< m^2n^4\)
\(\Rightarrow\left(\frac{mn^2-2}{n}\right)^2< P< \left(mn\right)^2\)
Xét \(\frac{mn^2-2}{n}-\left(mn-1\right)=\frac{n-2}{n}\ge0\) với \(\forall n\ge2\)
\(\Rightarrow\frac{mn^2-2}{n}\ge mn-1\)
\(\Rightarrow\left(mn-1\right)^2< P< \left(mn\right)^2\left(VL\right)\)
Kẹp giữa 2 số chính phương liên tiếp thì không tồn tại số chính phương nào.OK?
Giả sử \(m< n\)
\(\Rightarrow P>m^2n^2\left(3\right)\)
Xét \(m^2n^2-4m+4n-\left(mn+2\right)^2\)
\(=m^2n^2-4m+4n-m^2n^2-4mn-4\)
\(=n-m-mn-1=n\left(1-m\right)-m-1< 0\)
\(\Rightarrow P< \left(mn+2\right)^2\left(4\right)\)
Từ \(\left(3\right);\left(4\right)\Rightarrow\left(mn\right)^2< P< \left(mn+2\right)^2\)
Để P là số chính phương thì \(P=\left(mn+1\right)^2\)
\(\Rightarrow m^2n^2-4m+4n=m^2n^2+2mn+1\)
\(\Rightarrow-4m+4n-2mn=1\) quá VL
Với \(m=n\Rightarrow P=m^2n^2=\left(mn\right)^2\left(Lscp\right)\) cực kỳ HL:v
P/S:Ko chắc đâu nha.m thử làm bài 1 cấy.t cụng ra rồi nhưng coi cách m cho nó chắc:v Định dùng cách kẹp khác mà đề cho chặt quá:((
\(A\left(x\right)=Q\left(x\right)\left(x-1\right)+4\)(1)
\(A\left(x\right)=P\left(x\right)\left(x-3\right)+14\)(2)
\(A\left(x\right)=\left(x-1\right)\left(x-3\right)T\left(x\right)+F\left(x\right)\)(3)
Đặt : \(F\left(x\right)=ax+b\)
Với x=1 từ (1) và (3)
\(\hept{\begin{cases}A\left(1\right)=4\\A\left(1\right)=a+b\end{cases}}\)
\(\Rightarrow a+b=4\)(*)
Với x=3 từ (3) và (2)
\(\hept{\begin{cases}A\left(3\right)=14\\A\left(3\right)=3a+b\end{cases}}\)
\(\Rightarrow3a+b=14\)(**)
Từ (*) và (**)
\(\Rightarrow2a=10\Rightarrow a=5\Rightarrow b=-1\)
\(\Rightarrow F\left(x\right)=ax+b=5x-1\)
T lm r, ko bt có đúng ko:))
\(lim\dfrac{4n^5+n^3-5n+3}{\left(2n^2-3\right)\left(2n+1\right)^3}\)
\(lim\dfrac{4n^5+n^3-5n+3}{\left(2n^2-3\right)\left(2n+1\right)^3}\)
Lời giải:
\(\lim \frac{4n^5+n^3-5n+3}{(2n^2-3)(2n+1)^3}=\lim \frac{4+\frac{1}{n^2}-\frac{5}{n^4}+\frac{3}{n^5}}{(2-\frac{3}{n^2})(2+\frac{1}{n})^3}=\frac{4}{2.2^3}=\frac{1}{4}\)
Đúng 1
Bình luận (0)
Cho \(x=\frac{9m^2-4n^2-p^2}{8np}\)
\(y=\frac{\left(2n-p+3m\right)\left(2n-p-3m\right)}{3\left(4n^2+p^2-9m^2+4np\right)}\)
Tính \(Q=\left(6xy+1-2x-3y\right)^5\)
CMR: với mọi số tự nhiên n :
a) \(\left(x+1\right)^{2n}-x^{2n}-2x-1\) chia hết cho \(x\left(x+1\right)\left(2x+1\right)\)
b) \(x^{4n+2}+2x^{2n+1}+1\) chia hết cho \(\left(x+1\right)^2\)
c) \(\left(x+1\right)^{4n+2}+\left(x-1\right)^{4n+2}\) chia hết cho \(x^2+1\)
Tìm giới hạn dãy số sau
\(lim\dfrac{\left(2n-1\right)\left(3n^2+2\right)^3}{-2n^5+4n^3-1}\)
\(lim\left(3.2^{n+1}-5.3^n+7n\right)\)
\(\lim\dfrac{\left(2n-1\right)\left(3n^2+2\right)^3}{-2n^5+4n^3-1}=\lim\dfrac{\left(\dfrac{2n-1}{n}\right)\left(\dfrac{3n^2+2}{n^2}\right)^3}{\dfrac{-2n^5+4n^3-1}{n^7}}\)
\(=\lim\dfrac{\left(2-\dfrac{1}{n}\right)\left(3+\dfrac{2}{n^2}\right)^3}{-\dfrac{2}{n^2}+\dfrac{4}{n^4}-\dfrac{1}{n^7}}=-\infty\)
\(\lim3^n\left(6.\left(\dfrac{2}{3}\right)^n-5+\dfrac{7n}{3^n}\right)=+\infty.\left(-5\right)=-\infty\)
Đúng 2
Bình luận (0)