 mn trình bày rõ ra giúp e vs e cảm ơn
mn trình bày rõ ra giúp e vs e cảm ơn

Những câu hỏi liên quan
Trình bày cách giải rõ ràng, ct, đơn vị đầy đủ cho e vs ạ tại cô bắt có đầy đủ😅e cảm ơn mn
3.
\(F=\dfrac{k.\left|q_1.q_2\right|}{r^2}=\dfrac{9.10^9.\left|9.10^{-18}\right|}{0,1^2}=8,1.10^{-6}N\)
Đúng 1
Bình luận (0)
1.
\(F=\dfrac{k.\left|q_1.q_2\right|}{r^2}=\dfrac{9.10^9.\left|5.10^8.\left(-1,6.10^{-19}\right).5.10^8.\left(-1,6.10^{-19}\right)\right|}{0,02^2}=1,44.10^{-7}N\)
Đúng 0
Bình luận (0)
Vì sao ĐCSVN ra đời được coi là sự chuẩn bị đầu tiên có tính quyết định cho bước phát triển nhảy vọt mới của cách mạng Việt Nam?
(Trình bày tự luận giúp e với ạ. E cảm ơn mn nhìu)
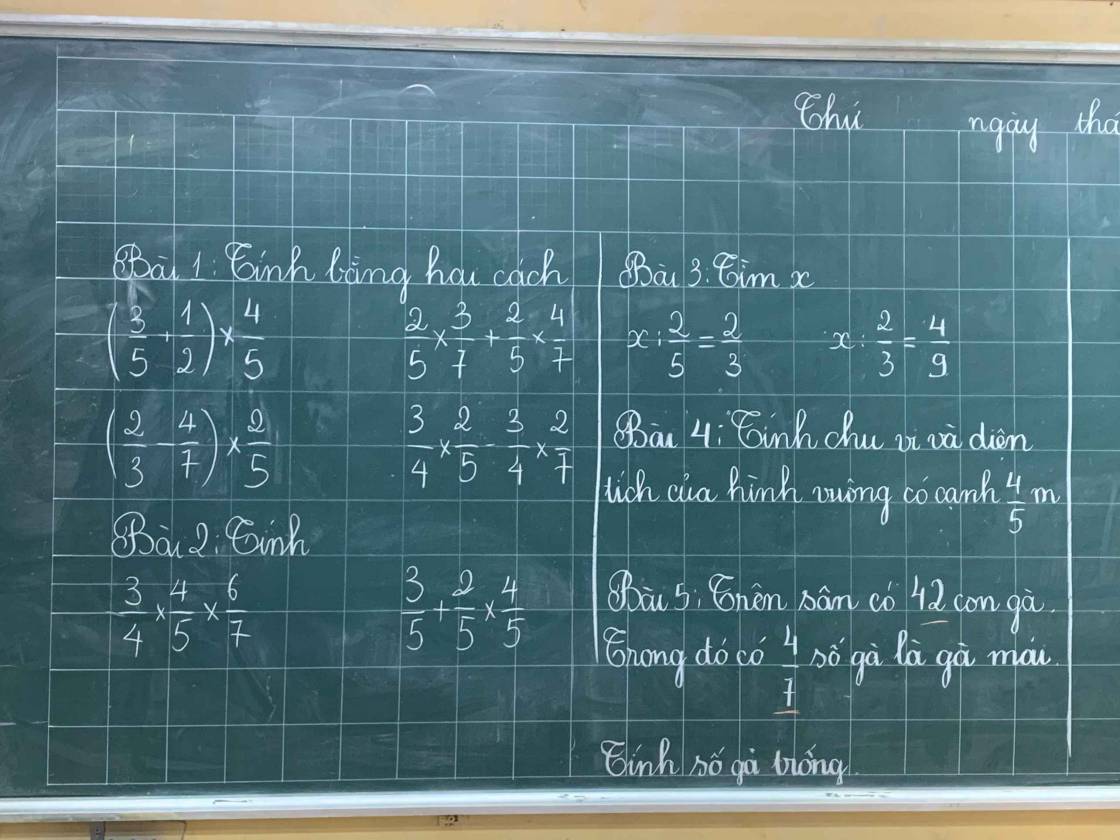 mn giúp e lm mấy bài này nha phải trình bày rõ ràng
mn giúp e lm mấy bài này nha phải trình bày rõ ràng
Bài 2:
a: \(=\dfrac{3}{5}\cdot\dfrac{6}{7}=\dfrac{18}{35}\)
b: =3/5+8/25
=15/25+8/25
=23/25
Bài 3:
a: =>x=2/3*2/5=4/25
b: =>x=4/9*2/3=8/27
Đúng 1
Bình luận (0)
Ôn tập
1.Tính
130050:452 19183:78 204 \(\times\) 1942
2.Tính
\(\dfrac{4}{9}+\dfrac{3}{7}\) \(\dfrac{7}{15}-\dfrac{11}{30}\)
2 bạn đầu tiên xong .Mn trình bày rõ ràng cho e ạ cảm ơn!
Bài 1:
\(130050:452=287\)(dư 326)
\(19183:78=245\)(dư 73)
\(204\times1942=396168\)
Bài 2:
\(\dfrac{4}{9}+\dfrac{3}{7}=\dfrac{28}{63}+\dfrac{27}{63}=\dfrac{55}{63}\)
\(\dfrac{7}{15}-\dfrac{11}{30}=\dfrac{14}{30}-\dfrac{11}{30}=\dfrac{3}{30}=\dfrac{1}{10}\)
Đúng 2
Bình luận (0)

mn giúp e vs e cảm ơn
Q=m.c.(t2-t1)
<=>13,68.1000=0,3.380.(t2-t1)
<=>t2-t1=120
=>t2=120+t1=120+20=140(độ C)
Nhiệt độ cuối của miếng đồng là 140 độ C
Đúng 0
Bình luận (0)

mn giúp e vs ,e cảm ơn
Độ tăng nhiệt độ của miếng chì :
\(\Delta t=\dfrac{Q}{m\cdot c}=\dfrac{4680}{0.3\cdot130}=120^0C\)
Đúng 1
Bình luận (0)
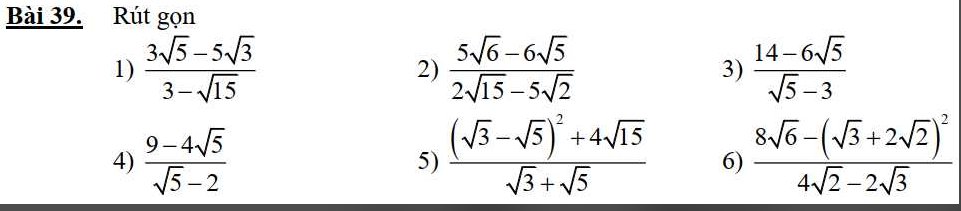 làm rõ ra giúp e ạ, e cảm ơn
làm rõ ra giúp e ạ, e cảm ơn
3: \(=\dfrac{\left(3-\sqrt{5}\right)^2}{\sqrt{5}-3}=\sqrt{5}-3\)
4: \(=\dfrac{\left(\sqrt{5}-2\right)^2}{\sqrt{5}-2}=\sqrt{5}-2\)
5: \(=\dfrac{8-2\sqrt{15}+4\sqrt{15}}{\sqrt{5}+\sqrt{3}}\)
\(=\dfrac{8+2\sqrt{15}}{\sqrt{5}+\sqrt{3}}=\dfrac{\left(\sqrt{5}+\sqrt{3}\right)^2}{\sqrt{5}+\sqrt{3}}=\sqrt{5}+\sqrt{3}\)
6:
\(=\dfrac{8\sqrt{6}-11-4\sqrt{6}}{4\sqrt{2}-2\sqrt{3}}\)
\(=\dfrac{4\sqrt{6}-11}{4\sqrt{2}-2\sqrt{3}}=\dfrac{\sqrt{3}-2\sqrt{2}}{2}\)
Đúng 1
Bình luận (0)
1) \(\dfrac{3\sqrt{5}-5\sqrt{3}}{3-\sqrt{15}}=\dfrac{\sqrt{15}\left(\sqrt{3}-\sqrt{5}\right)}{\sqrt{3}\left(\sqrt{3}-\sqrt{5}\right)}=\sqrt{15}\)
2) \(\dfrac{5\sqrt{6}-6\sqrt{5}}{2\sqrt{15}-5\sqrt{2}}=\dfrac{\sqrt{30}\left(\sqrt{5}-\sqrt{6}\right)}{\sqrt{10}\left(\sqrt{6}-\sqrt{5}\right)}=-\sqrt{3}\)
3) \(\dfrac{14-6\sqrt{5}}{\sqrt{5}-3}=\dfrac{\left(3-\sqrt{5}\right)^2}{\sqrt{5}-3}=\sqrt{5}-3\)
4) \(\dfrac{9-4\sqrt{5}}{\sqrt{5}-2}=\dfrac{\left(2-\sqrt{5}\right)^2}{\sqrt{5}-2}=\sqrt{5}-2\)
5) \(\dfrac{\left(\sqrt{3}-\sqrt{5}\right)^2+4\sqrt{15}}{\sqrt{3}+\sqrt{5}}=\dfrac{\sqrt{3}+\sqrt{5}}{\sqrt{3}+\sqrt{5}}=1\)
6) \(\dfrac{8\sqrt{6}-\left(\sqrt{3}+2\sqrt{2}\right)^2}{4\sqrt{2}-2\sqrt{3}}=\dfrac{8\sqrt{6}-11-4\sqrt{6}}{4\sqrt{2}-2\sqrt{3}}\)
\(=\dfrac{4\sqrt{6}-11}{2\left(2\sqrt{2}-\sqrt{3}\right)}=\dfrac{(\sqrt{3}-2\sqrt{2})^2}{2\left(\sqrt{3}-2\sqrt{2}\right)}=\dfrac{\sqrt{3}-2\sqrt{2}}{2}\)
Đúng 1
Bình luận (0)
Giúp e vs ạ e cảm ơn mn
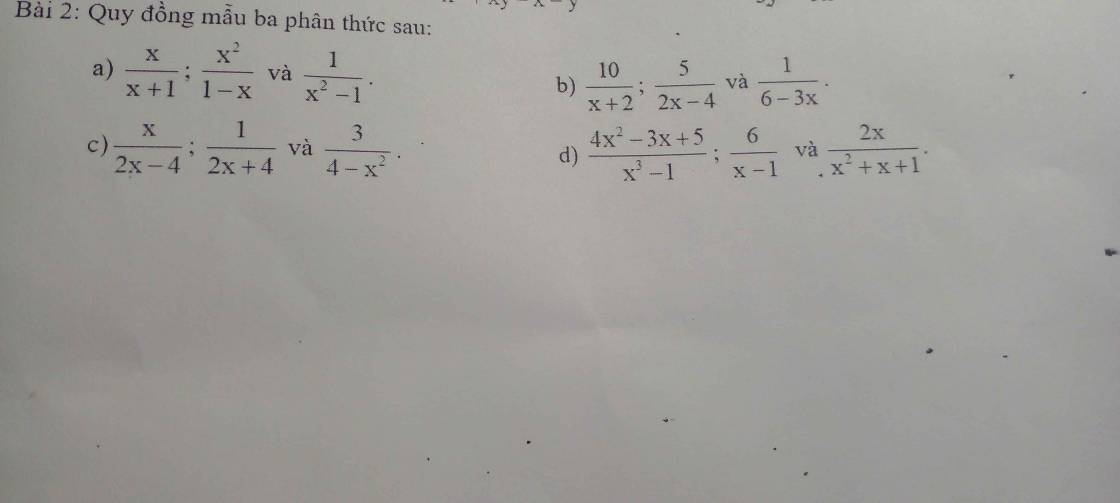 giúp e vs mn ơi . E xin "trịnh trọng" cảm ơn mn ạ
giúp e vs mn ơi . E xin "trịnh trọng" cảm ơn mn ạ
câu a, \(\dfrac{x}{x+1}\); \(\dfrac{x^2}{1-x}\); \(\dfrac{1}{x^2-1}\) (đk \(x\)≠ -1; 1)
\(x^2\) - 1 = ( \(x\) - 1).(\(x\) + 1)
\(\dfrac{x}{x+1}\) = \(\dfrac{x.\left(x-1\right)}{\left(x+1\right).\left(x-1\right)}\);
\(\dfrac{x^2}{1-x}\) = \(\dfrac{-x^2}{x-1}\)= \(\dfrac{-x^2.\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)
\(\dfrac{1}{x^2-1}\) = \(\dfrac{1}{\left(x-1\right)\left(x+1\right)}\)
b, \(\dfrac{10}{x+2}\); \(\dfrac{5}{2x-4}\); \(\dfrac{1}{6-3x}\) (đk \(x\) ≠ -2; 2)
2\(x-4\) = 2.(\(x\) - 2); 6 - 3\(x\) = - 3.(\(x\) - 2)
\(\dfrac{10}{x+2}\) = \(\dfrac{10.2.3\left(x-2\right)}{2.3\left(x+2\right)\left(x-2\right)}\) = \(\dfrac{60\left(x-2\right)}{6\left(x-2\right)\left(x+2\right)}\)
\(\dfrac{5}{2x-4}\) = \(\dfrac{5.3\left(x+2\right)}{2.3\left(x-2\right).\left(x+2\right)}\) = \(\dfrac{15.\left(x+2\right)}{6.\left(x-2\right)\left(x+2\right)}\)
\(\dfrac{1}{6-3x}\) = \(\dfrac{-1}{3.\left(x-2\right)}\) = \(\dfrac{-1.\left(x+2\right)}{3.2.\left(x-2\right)\left(x+2\right)}\) = \(\dfrac{-2.\left(x+2\right)}{6.\left(x-2\right).\left(x+2\right)}\)
Đúng 1
Bình luận (0)
c, \(\dfrac{x}{2x-4}\); \(\dfrac{1}{2x+4}\) và \(\dfrac{3}{4-x^2}\) đk \(x\) ≠ 2; -2
\(\dfrac{x}{2x-4}\) = \(\dfrac{x}{2.\left(x-2\right)}\) = \(\dfrac{x.\left(x+2\right)}{2.\left(x-2\right).\left(x+2\right)}\)
\(\dfrac{1}{2x+4}\) = \(\dfrac{1}{2.\left(x+2\right)}\) = \(\dfrac{\left(x-2\right)}{2.\left(x+2\right).\left(x-2\right)}\)
\(\dfrac{3}{4-x^2}\) = \(\dfrac{-3}{\left(x-2\right)\left(x+2\right)}\) = \(\dfrac{-6}{2.\left(x-2\right)\left(x+2\right)}\)
Đúng 1
Bình luận (0)
\(\dfrac{4x^2-3x+5}{x^3-1}\) = \(\dfrac{4x^2-3x+5}{\left(x-1\right)\left(x^2+x+1\right)}\) Đk \(x\) ≠ 1
\(\dfrac{6}{x-1}\) = \(\dfrac{6.\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(\dfrac{2x}{x^2+x+1}\) = \(\dfrac{2x.\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
Đúng 1
Bình luận (0)



















