3: \(=\dfrac{\left(3-\sqrt{5}\right)^2}{\sqrt{5}-3}=\sqrt{5}-3\)
4: \(=\dfrac{\left(\sqrt{5}-2\right)^2}{\sqrt{5}-2}=\sqrt{5}-2\)
5: \(=\dfrac{8-2\sqrt{15}+4\sqrt{15}}{\sqrt{5}+\sqrt{3}}\)
\(=\dfrac{8+2\sqrt{15}}{\sqrt{5}+\sqrt{3}}=\dfrac{\left(\sqrt{5}+\sqrt{3}\right)^2}{\sqrt{5}+\sqrt{3}}=\sqrt{5}+\sqrt{3}\)
6:
\(=\dfrac{8\sqrt{6}-11-4\sqrt{6}}{4\sqrt{2}-2\sqrt{3}}\)
\(=\dfrac{4\sqrt{6}-11}{4\sqrt{2}-2\sqrt{3}}=\dfrac{\sqrt{3}-2\sqrt{2}}{2}\)
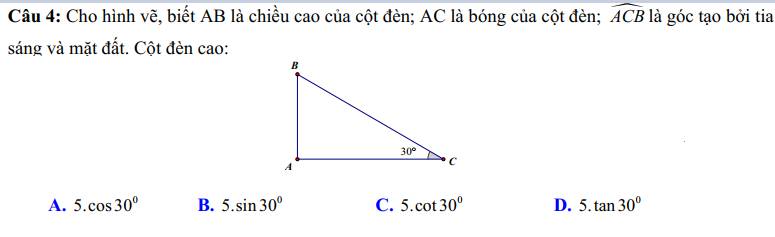
1) \(\dfrac{3\sqrt{5}-5\sqrt{3}}{3-\sqrt{15}}=\dfrac{\sqrt{15}\left(\sqrt{3}-\sqrt{5}\right)}{\sqrt{3}\left(\sqrt{3}-\sqrt{5}\right)}=\sqrt{15}\)
2) \(\dfrac{5\sqrt{6}-6\sqrt{5}}{2\sqrt{15}-5\sqrt{2}}=\dfrac{\sqrt{30}\left(\sqrt{5}-\sqrt{6}\right)}{\sqrt{10}\left(\sqrt{6}-\sqrt{5}\right)}=-\sqrt{3}\)
3) \(\dfrac{14-6\sqrt{5}}{\sqrt{5}-3}=\dfrac{\left(3-\sqrt{5}\right)^2}{\sqrt{5}-3}=\sqrt{5}-3\)
4) \(\dfrac{9-4\sqrt{5}}{\sqrt{5}-2}=\dfrac{\left(2-\sqrt{5}\right)^2}{\sqrt{5}-2}=\sqrt{5}-2\)
5) \(\dfrac{\left(\sqrt{3}-\sqrt{5}\right)^2+4\sqrt{15}}{\sqrt{3}+\sqrt{5}}=\dfrac{\sqrt{3}+\sqrt{5}}{\sqrt{3}+\sqrt{5}}=1\)
6) \(\dfrac{8\sqrt{6}-\left(\sqrt{3}+2\sqrt{2}\right)^2}{4\sqrt{2}-2\sqrt{3}}=\dfrac{8\sqrt{6}-11-4\sqrt{6}}{4\sqrt{2}-2\sqrt{3}}\)
\(=\dfrac{4\sqrt{6}-11}{2\left(2\sqrt{2}-\sqrt{3}\right)}=\dfrac{(\sqrt{3}-2\sqrt{2})^2}{2\left(\sqrt{3}-2\sqrt{2}\right)}=\dfrac{\sqrt{3}-2\sqrt{2}}{2}\)

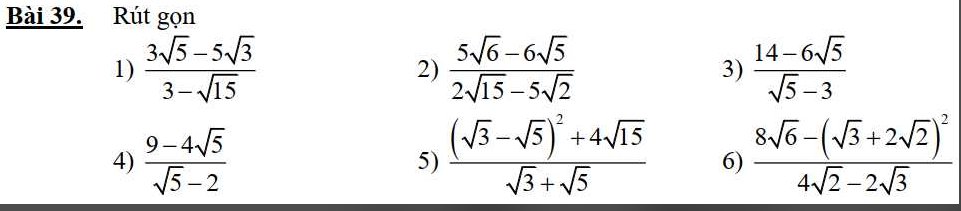 làm rõ ra giúp e ạ, e cảm ơn
làm rõ ra giúp e ạ, e cảm ơn




 làm rõ giúp e ạ, e cảm ơnn
làm rõ giúp e ạ, e cảm ơnn








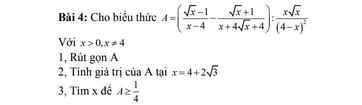 Mn giúp e với
Mn giúp e với