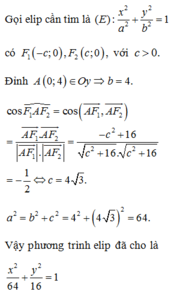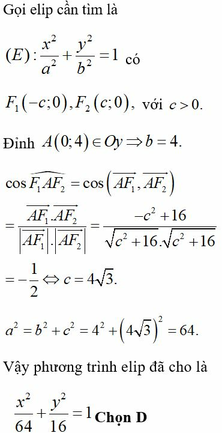Viết phương trình chính tắc của elip biết tiêu điểm F1 = (-√3;0) và đi qua M (√3 ; ½)?
Những câu hỏi liên quan
Lập phương trình chính tắc của elip trong trường hợp sau: Elip có một tiêu điểm là
F
1
-
3
;
0
và điểm
M
1
;
3
2
nằm trên elip...
Đọc tiếp
Lập phương trình chính tắc của elip trong trường hợp sau: Elip có một tiêu điểm là F 1 - 3 ; 0 và điểm M 1 ; 3 2 nằm trên elip.
Gọi Elip cần tìm có dạng : (E) :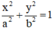 
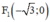là tiêu điểm của (E) ⇒ a2 – b2 = 3 ⇒ a2 = b2 + 3
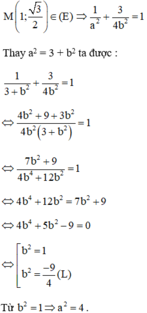
Phương trình chính tắc của Elip là :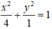 
Đúng 1
Bình luận (0)
Trong mặt phẳng Oxy , viết phương trình chính tắc của Elip có một tiêu điểm là F1(-2;0) và đi qua điểm M(2;3)
F1(-2;0) nên c=-2
=>c^2=4
=>c^2=a^2-b^2=4
=>a^2=b^2+4
(E): x^2/a^2+y^2/b^2=1
Thay x=2 và y=3 vào (E), ta được:
2^2/a^2+3^2/b^2=1
=>4/a^2+9/b^2=1
=>\(\dfrac{4}{b^2+4}+\dfrac{9}{b^2}=1\)
=>\(\dfrac{13b^2+36}{b^2\left(b^2+4\right)}=1\)
=>b^4+4b^2-13b^2-36=0
=>b^2=12
=>b=2căn 3
=>a=4
=>(E): x^2/16+y^2/12=1
Đúng 1
Bình luận (1)
Cho elip (E) có một đỉnh là A( 5; 0) và có 1 tiêu điểm F1(- 4; 0). Phương trình chính tắc của elip là: A.
x
2
25
+
y
2
16
1.
B.
x
2
5
+
y
2
4
1.
C. ...
Đọc tiếp
Cho elip (E) có một đỉnh là A( 5; 0) và có 1 tiêu điểm F1(- 4; 0). Phương trình chính tắc của elip là:
A. x 2 25 + y 2 16 = 1.
B. x 2 5 + y 2 4 = 1.
C. x 2 25 + y 2 9 = 1.
D. x 5 + y 4 = 1.
Trong mặt phẳng tọa độ Oxy, cho elip có đỉnh A(0;4) nhìn hai tiêu điểm
F
1
,
F
2
dưới một góc bằng
120
°
. Phương trình chính tắc của elip đã cho là
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho elip có đỉnh A(0;4) nhìn hai tiêu điểm F 1 , F 2 dưới một góc bằng 120 ° . Phương trình chính tắc của elip đã cho là
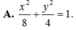
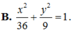
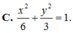
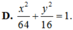
Trong mặt phẳng tọa độ Oxy, cho elip có đỉnh A(0;4) nhìn hai tiêu điểm
F
1
,
F
2
dưới một góc bằng
120
∘
. Phương trình chính tắc của elip đã cho là A.
x
2
8
+
y
2
4
1
B.
x...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho elip có đỉnh A(0;4) nhìn hai tiêu điểm F 1 , F 2 dưới một góc bằng 120 ∘ . Phương trình chính tắc của elip đã cho là
A. x 2 8 + y 2 4 = 1
B. x 2 36 + y 2 9 = 1
C. x 2 6 + y 2 3 = 1
D. x 2 64 + y 2 16 = 1
Viết phương trình chính tắc Elip khi biết 1 tiêu điểm F2(5;0) và đi qua 1 điểm M(0;3)
F2(5;0)
=>c=5
(E): x^2/a^2+y^2/b^2=1
Thay x=0 và y=3 vào (E), ta được:
9/b^2=1
=>b=3
c^2=a^2-b^2
=>a^2=5^2+3^2=34
=>(E): x^2/34+y^2/9=1
Đúng 0
Bình luận (0)
Cho elip (E) có các tiêu điểm
F
1
-
5
;
0
,
F
2
5
;
0
và một điểm M nằm trên (E) sao cho chu vi của tam giác
M
F
1
F
2
bằng 30. Khi đó phương trình chính tắc của elip là: A. ...
Đọc tiếp
Cho elip (E) có các tiêu điểm F 1 - 5 ; 0 , F 2 5 ; 0 và một điểm M nằm trên (E) sao cho chu vi của tam giác M F 1 F 2 bằng 30. Khi đó phương trình chính tắc của elip là:
A. x 2 75 + y 2 100 = 1
B. 100 x 2 + 75 y 2 = 1
C. 75 x 2 + 100 y 2 = 1
D. x 2 100 + y 2 75 = 1
viết phương trình chính tắc của elip các trường hợp sau 1. elip đi qua điểm M(0;3) và có tiêu điểm F2(5;0) 2. Elip đi qua hai điểm A(7;0), B(0;3) 3. Elip đi qua hai điểm A(0;1), N(1; căn 3 / 2)
1: (E): x^2/a^2+y^2/b^2=1
Thay x=0 và y=3 vào (E), ta được:
3^2/b^2=1
=>b^2=9
=>b=3
F2(5;0)
=>c=5
=>\(\sqrt{a^2-9}=5\)
=>a^2-9=25
=>a^2=34
=>\(a=\sqrt{34}\)
=>x^2/34+y^2/9=1
2: Thay x=7 và y=0 vào (E), ta được:
7^2/a^2+0^2/b^2=0
=>a^2=49
=>a=7
Thay x=0 và y=3 vào (E), ta được:
0^2/a^2+3^2/b^2=1
=>b^2=9
=>b=3
=>(E): x^2/49+y^2/9=1
3: Thay x=0 và y=1 vào (E), ta được:
1/y^2=1
=>y=1
=>(E): x^2/a^2+y^2/1=1
Thay x=1 và y=căn 3/2 vào (E), ta được:
1^2/a^2+3/4=1
=>1/a^2=1/4
=>a^2=4
=>a=2
=>(E); x^2/4+y^2/1=1
Đúng 2
Bình luận (0)
Viết phương trình chính tắc của elip đi qua điểm A(0;-4) và có 1 tiêu điểm F2(3;0)
Gọi ptr chính tắc của `(E)` có dạng: `[x^2]/[a^2]+[y^2]/[b^2]=1`
Thay `A(0;-4)` vào `(E)` có:
`16/[b^2]=1<=>b^2=16`
Vì `F_2 (3;0)=>c=3=>c^2=9`
Ta có: `a^2=b^2+c^2`
`<=>a^2=16+9`
`<=>a^2=25`
Vậy ptr chính tắc của `(E)` là: `[x^2]/25+[y^2]/16=1`
Đúng 2
Bình luận (0)