Các câu hỏi tương tự
Elip có một tiêu điểm F(-2; 0) và tích độ dài trục lớn với trục bé bằng
12
5
. Phương trình chính tắc của elip là: A.
x
2
9
+
y
2
5
1.
B.
x
2
36
+
y
2
20...
Đọc tiếp
Elip có một tiêu điểm F(-2; 0) và tích độ dài trục lớn với trục bé bằng 12 5 . Phương trình chính tắc của elip là:
A. x 2 9 + y 2 5 = 1.
B. x 2 36 + y 2 20 = 1.
C. x 2 144 + y 2 5 = 1.
D. x 2 45 + y 2 16 = 1.
Trong mặt phẳng tọa độ $Oxy$, cho elip $\left( E \right):\dfrac{{ x^2}}{4}+{{y}^2}=1.$ Gọi ${{F}_{1}};{{F}_2}$ là hai tiêu điểm của $\left( E \right)$ và điểm $M\in \left( E \right)$ sao cho $M{{F}_{1}}\bot M{{F}_2}$. Tính $M{{F}_{1}}^2+M{{F}_2}^2$ và diện tích $\Delta M{{F}_{1}}{{F}_2}.$
Cho elip (E) có một đỉnh là A( 5; 0) và có 1 tiêu điểm F1(- 4; 0). Phương trình chính tắc của elip là: A.
x
2
25
+
y
2
16
1.
B.
x
2
5
+
y
2
4
1.
C. ...
Đọc tiếp
Cho elip (E) có một đỉnh là A( 5; 0) và có 1 tiêu điểm F1(- 4; 0). Phương trình chính tắc của elip là:
A. x 2 25 + y 2 16 = 1.
B. x 2 5 + y 2 4 = 1.
C. x 2 25 + y 2 9 = 1.
D. x 5 + y 4 = 1.
Trong mặt phẳng với hệ trục tọa độ $Oxy$, cho elip $\left( E \right)$ có phương trình: $\dfrac{{ x^2}}{9}+\dfrac{{{y}^2}}{4}=1$. Gọi ${{F}_{1}}, \, {{F}_2}$ là hai tiêu điểm của $\left( E \right)$. Tìm điểm $M$thuộc $\left( E \right)$ sao cho góc $\widehat{{{F}_{1}}M{{F}_2}}$ bằng ${{90}^{\circ}}$.
Trên mặt phẳng Oxy cho tam giác MNP có diện tích bằng 2, đường thẳng đi qua M và P có phương trình x - y = 0. Tìm tọa độ trung điểm E của cạnh MN biết F(2;1) là trung điểm của cạnh NP.
Cho Elip có các tiêu điểm F1(-4;0) và F2(4;0) và một điểm M nằm trên (E) biết rằng chu vi của tam giác MF1F2 bằng 18. Lúc đó tâm sai của (E) là:
Đọc tiếp
Cho Elip có các tiêu điểm F1(-4;0) và F2(4;0) và một điểm M nằm trên (E) biết rằng chu vi của tam giác MF1F2 bằng 18. Lúc đó tâm sai của (E) là:
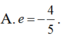
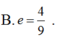
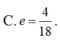
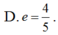
Cho Elip (E)
x
2
16
+
y
2
12
1
và điểm M nằm trên (E) . Nếu điểm M có hoành độ bằng 1 thì các khoảng cách từ M tới 2 tiêu điểm của (E) bằng A.
4
±
2
B. 3 và 5. C. 3,5 và 4,5 D....
Đọc tiếp
Cho Elip (E) x 2 16 + y 2 12 = 1 và điểm M nằm trên (E) . Nếu điểm M có hoành độ bằng 1 thì các khoảng cách từ M tới 2
tiêu điểm của (E) bằng
A. 4 ± 2
B. 3 và 5.
C. 3,5 và 4,5
D. 4 ± 2 2
Cho elip (E) có phương trình
x
2
m
2
+
y
2
6
m
1
. Giá trị của m để phương trình đó là phương trình chính tắc của một elip có tiêu cự bằng 8 là: A. m - 2 B. m 8 C. m - 2 hoặc m 8 D. không tồn tại m
Đọc tiếp
Cho elip (E) có phương trình x 2 m 2 + y 2 6 m = 1 . Giá trị của m để phương trình đó là phương trình chính tắc của một elip có tiêu cự bằng 8 là:
A. m = - 2
B. m = 8
C. m = - 2 hoặc m = 8
D. không tồn tại m
Cho f(x)=x^2 -2(m-2)x+m+10. Định m để:
a. Phương trình f(x)=0 có một nghiệm x= 1 và tính nghiệm kia
b. Phương trình f(x)=0 có nghiệm kép. Tính nghiệm kép đó.
c. Tìm m để phương trình f(x)=0 có 2 nghiệm âm phân biệt.
d. Tìm m để f(x)<0 có nghiệm đúng với mọi xϵR








