gieo đồng xu 4 lần liên tiếp.tính xác suất có ít nhất 2 lần liên tiếp xuất hiện mặt ngửa

Những câu hỏi liên quan
gieo ngẫu nhiên một đồng xu 3 lần liên tiếp. Tính xác suất của các biến cố sau: A:" Ba lần gieo xuất hiện như nhau" B:" mặt ngửa xuất hiện đúng một lần" C: "lần thứ hai xuất hiện mặt sấp" D:"mặt ngửa xuất hiện ít nhất một lần"
a: n(A)=2
n(omega)=2*2*2=8
=>P(A)=2/8=1/4
b: B={(NSS); (SNS); (SSN)}
=>n(B)=3
=>P(B)=3/8
c: C={NSS; NSN; SSN; SSS}
=>n(C)=4
=>P(C)=4/8=1/2
d: D={NSN; NNS; NNN; SNN; NSS; SNS; SSN}
=>n(D)=6
=>P(D)=6/8=3/4
Đúng 2
Bình luận (0)
Gieo một đồng xu cân đối liên tiếp bốn lần.
a) Vẽ sơ đồ hình cây mô tả không gian mẫu.
b) Tính xác suất để trong bốn lần gieo đó có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa.
a) Kí hiệu S là đồng xu ra mặt sấp và N là đồng xu ra mặt ngửa. Ta có sơ đồ cây
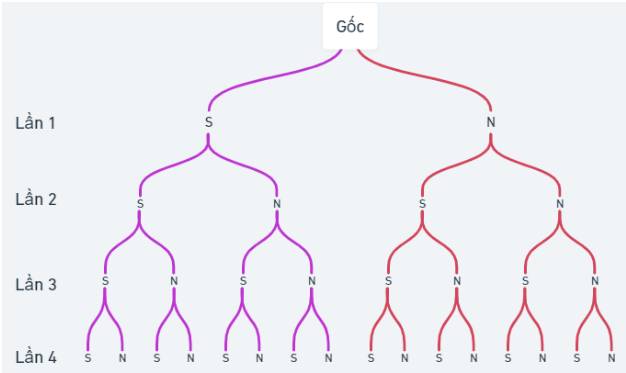
Dựa vào sơ đồ cây ta suy ra \(n\left( \Omega \right) = 16\).
b) Gọi A là biến cố: “gieo đồng xu 4 lần có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa”
Suy ra \(A = \left\{ {SSNN;SNSN;SNNS;NSSN;NSNS;NNSS} \right\}\). Suy ra \(n\left( A \right) = 6\). Vậy\(P\left( A \right) = \frac{6}{{16}} = \frac{3}{8}\).
Đúng 0
Bình luận (0)
Trong trò chơi gieo ngẫu nhiên đồng xu nhiều lần liên tiếp, hỏi phải gieo ít nhất bao nhiêu lần để xác suất được mặt ngửa nhỏ hơn 1 100 .
A. 7
B. 8
C. 9
D. 6
Trong trò chơi gieo ngẫu nhiên đồng xu nhiều lần liên tiếp, hỏi phải gieo ít nhất bao nhiêu lần để xác suất được mặt ngửa nhỏ hơn 1 100 .
A. 7
B. 8
C. 9
D. 6
Đáp án A
Xác suất để gieo n lần đều mặt ngửa là 1 2 n . Từ đo 1 2 n < 1 100 ⇔ n < log 1 2 1 100 ⇒ n ≥ 7 .
Ta cần gieo ít nhất 7 lần
Đúng 0
Bình luận (0)
Trong trò chơi gieo ngẫu nhiên đồng xu nhiều lần liên tiếp, hỏi phải gieo ít nhất bao nhiêu lần để xác suất được mặt ngửa nhỏ hơn
1
100
. A. 7 B. 8 C. 9 D. 6
Đọc tiếp
Trong trò chơi gieo ngẫu nhiên đồng xu nhiều lần liên tiếp, hỏi phải gieo ít nhất bao nhiêu lần để xác suất được mặt ngửa nhỏ hơn 1 100 .
A. 7
B. 8
C. 9
D. 6
Đáp án A
Xác suất để gieo n lần đều mặt ngửa là 1 2 n . Từ đó
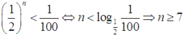
Ta cần gieo ít nhất 7 lần.
Đúng 0
Bình luận (0)
: Nếu tung một lúc 2 đồng xu 5 lần liên tiếp có 1 lần xuất hiện mặt SS; 1 lần xuất
hiện mặt NN; 2 lần xuất hiện mặt SN.
a. Các kết quả có thể xảy ra khi gieo 2 đồng xu 5 lần? b. Tính xác suất thực nghiệm xuất hiện mặt SS?
c. Tính xác suất thực nghiệm xuất hiện mặt NN? d. Tính xác suất thực nghiệm xuất hiện mặt SN? e. Tính xác suất thực nghiệm xuất hiện mặt NS?
gieo 2 đồng xu A và B một cách độc lập . đồng xu A chế tạo cân đối , đồng xu B chế tạo không cân đối nên xác suất xuất hiện mặt sấp gấp 3 lần xác suất xuất hiện mặt ngửa . tính xác suất để :
a) khi gieo 2 đồng xu 1 lần thì cả 2 đồng xu đều ngửa .
b) khi gieo 2 đồng xu 2 lần thì 2 lần cả 2 đồng xu đều ngửa .
xác suất mặt ngửa của đồng A là 1/2,của đồng B là 1/4
1.Gieo 2 đồng xu 1 lần,xác suất cả hai đều ngửa là 1/2*1/4 = 1/8
2.2 lần đều ngửa : 1/2*1/4*1/2*1/4 = 1/64
1.Gieo 2 đồng xu 1 lần,xác suất cả hai đều ngửa là 1/2*1/4 = 1/8
2.2 lần đều ngửa : 1/2*1/4*1/2*1/4 = 1/64
Đúng 0
Bình luận (0)
Nếu tung một lúc 2 đồng xu 5 lần liên tiếp có 1 lần xuất hiện mặt SS; 1 lần xuấthiện mặt NN; 2 lần xuất hiện mặt SN.a. Các kết quả có thể xảy ra khi gieo 2 đồng xu 5 lần? b. Tính xác suất thực nghiệm xuất hiện mặt SS?c. Tính xác suất thực nghiệm xuất hiện mặt NN? d. Tính xác suất thực nghiệm xuất hiện mặt SN? e. Tính xác suất thực nghiệm xuất hiện mặt NS? Nếu tung một lúc 2 đồng xu 5 lần liên tiếp có 1 lần xuất hiện mặt SS; 1 lần xuấthiện mặt NN; 2 lần xuất hiện mặt SN.a. Các kết quả có thể xảy...
Đọc tiếp
Nếu tung một lúc 2 đồng xu 5 lần liên tiếp có 1 lần xuất hiện mặt SS; 1 lần xuất
hiện mặt NN; 2 lần xuất hiện mặt SN.
a. Các kết quả có thể xảy ra khi gieo 2 đồng xu 5 lần? b. Tính xác suất thực nghiệm xuất hiện mặt SS?
c. Tính xác suất thực nghiệm xuất hiện mặt NN? d. Tính xác suất thực nghiệm xuất hiện mặt SN? e. Tính xác suất thực nghiệm xuất hiện mặt NS? Nếu tung một lúc 2 đồng xu 5 lần liên tiếp có 1 lần xuất hiện mặt SS; 1 lần xuất
hiện mặt NN; 2 lần xuất hiện mặt SN.
a. Các kết quả có thể xảy ra khi gieo 2 đồng xu 5 lần? b. Tính xác suất thực nghiệm xuất hiện mặt SS?
c. Tính xác suất thực nghiệm xuất hiện mặt NN? d. Tính xác suất thực nghiệm xuất hiện mặt SN? e. Tính xác suất thực nghiệm xuất hiện mặt NS?
Câu 8. Nếu gieo một con xúc xắc 11 lần liên tiếp, có 6 lần xuất hiện mặt 2 chấm thì xác suấtthực nghiệm xuất hiện mặt 2 chấm là:A.511. B.611 . C.211 . D.2 5.Câu 9. Nếu tung đồng xu 15 lần liên tiếp, có 7 lần xuất hiện mặt S thì xác suất thực nghiệmxuất hiện mặt N là:A.715 B.7 8C.8 7D.815Câu 10. Một hộp có 10 chiếc thẻ được đánh số từ 1 đến 10. Rút ngẫu nhiên một chiếc thẻ từtrong hộp, ghi lại số của thẻ rút được và bỏ lại thẻ đó vào hộp. Sau 20 lần rút thẻ liên tiếp,nhận thấy có 4 lần lấy được t...
Đọc tiếp
Câu 8. Nếu gieo một con xúc xắc 11 lần liên tiếp, có 6 lần xuất hiện mặt 2 chấm thì xác suất
thực nghiệm xuất hiện mặt 2 chấm là:
A.
5
11. B.
6
11 . C.
2
11 . D.
2 5
.
Câu 9. Nếu tung đồng xu 15 lần liên tiếp, có 7 lần xuất hiện mặt S thì xác suất thực nghiệm
xuất hiện mặt N là:
A.
7
15 B.
7 8
C.
8 7
D.
8
15
Câu 10. Một hộp có 10 chiếc thẻ được đánh số từ 1 đến 10. Rút ngẫu nhiên một chiếc thẻ từ
trong hộp, ghi lại số của thẻ rút được và bỏ lại thẻ đó vào hộp. Sau 20 lần rút thẻ liên tiếp,
nhận thấy có 4 lần lấy được thẻ đánh số 6. Xác suất thực nghiệm xuất hiện thẻ đánh số 6 là:
A.
1 5
B.
16
20 C.
1 2
D. Đáp án khác
Câu 11. Một hộp chứa 5 cái thẻ được đánh số 1, 2, 3, 4, 5. Lấy ngẫu nhiên một thẻ. Tập hợp
các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là:
A. 1; 2; 3; 4. B. {1; 2; 3; 4; 5}. C. 1; 2; 3; 4; 5. D. {1; 2; 3; 4}.
Câu 12. Một hộp có 4 chiếc bánh, trong đó có 1 chiếc bánh vị va ni, 1 chiếc bánh vị ca cao,
1 chiếc bánh vị chocolate, 1 chiếc bánh vị dừa. Lấy ngẫu nhiên một chiếc bánh trong hộp. Có
mấy kết quả có thể xảy ra đối với vị của chiếc bánh trong hộp được lấy ra.
A. 1 B. 2 . C. 3 . D. 4.
Câu 13. Các cặp phân số bằng nhau là:
A.
6 7
và
24
28
B.
3 4
và
6
8
C.
7
2
và
21
6 D.
0 7
và
14
2
Xem thêm câu trả lời