Đáp án A
Xác suất để gieo n lần đều mặt ngửa là 1 2 n . Từ đó
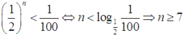
Ta cần gieo ít nhất 7 lần.
Đáp án A
Xác suất để gieo n lần đều mặt ngửa là 1 2 n . Từ đó
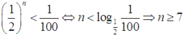
Ta cần gieo ít nhất 7 lần.
Gieo ngẫu nhiên một con súc sắc cân đối, đồng chất liên tiếp 3 lần. Xác suất để được mặt có 6 chấm chỉ xuất hiện trong lần gieo thứ 3 là bao nhiêu?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. Khác.
Gieo ngẫu nhiên ba đồng xu phân biệt một lần. Kí hiệu S, N lần lượt chỉ đồng xu lật sấp, lật ngửa
b) Xác định biến cố C:”có ít nhất hai đồng tiền xuất hiện mặt ngửa”
A. C={NNS,NSN,SNN}
B. C={NNS,NSN,SNN,NNN}
C. C={N,N,S}
D. C={N,N,N}
Gieo một con súc sắc cân đối và đồng chất hai lần liên tiếp. Tính xác suất để 1) lần thứ nhất được số chấm chẵn và lần thứ hai được số chấm lẻ. 2) hai lần gieo có số chấm như nhau. 3) mặt 6 chấm xuất hiện ít nhất một lần. 4) tổng số chấm xuất hiện trong hai lần gieo bé hơn 10.
Cho phép thử là “gieo 10 đồng xu phân biệt” và xét sự xuất hiện mặt sấp và mặt ngửa của các đồng xu. Xác suất để có đúng một lần suất hiện mặt ngửa là
A . 5 512
B . 1 1024
C . 11 512
D . 99 1024
gieo một đồng xu cân đối đồng chất liên tiếp 2 lần .xác xuất đề cả 2 lần xuất hiện măyj ngửa là
a 0,75
b. 1/3
c. 0,25
d .0,5
Gieo một đồng tiền liên tiếp 3 lần. Tính xác suất của biến cố A:”ít nhất một lần xuất hiện mặt sấp”
A. P(A)=1/2.
B. P(A)=3/8.
C. P(A)=7/8.
D. P(A)=1/4.
Gieo một đồng tiền liên tiếp cho đến khi xuất hiện mặt sấp hoặc cả 4 lần ngửa thì dừng lại.
a. Mô tả không gian mẫu.
b. Xác định các biến cố.
A: "Số lần gieo không vượt quá 3"
B: "Số lần gieo là 4"
Gieo ngẫu nhiên một con súc sắc 3 lần liên tiếp. Gọi a,b,c lần lượt là số chấm xuất hiện ở 3 lần gieo. Xác suất của biến cố “ số a b c ¯ chia hết cho 45” là
A . 1 216
B . 1 54
C . 1 72
D . 1 108
Gieo đồng xu 4 lần. Tính xác suất a/ Lần 3, 4 được mặt sấp b/ Có 1 lần được mặt sấp