Cho hình chóp SABCD có đáy là hình thang vuông tại A, AB=BC=a; AD= 2a; SA vuông với đáy; SA = a. M,N lần lượt là trung điểm của SB, CD. Tính:
a, (SC, đáy)
b, (SB, SAC)
c, (SD, SAB)
d, (SN, SAC)
e, (SA, SCD)
f, (SA, SBC)
h, (MN, SCA) (xác định góc)
Những câu hỏi liên quan
cho hình chóp SABCD có đáy là hình thang vuông tại A và D, SA vuông góc với đáy, SA=SD=a , AB=2a. Tính \(d_{\left(AB,BC\right)}\)
Cho hình chóp SABCD có đáy là hình thang vuông tại A, B, AD a, AB2a, BC3a,SA2a . H là trung điểm cạnh AB,SH là đường cao của hình chóp SABCD Tính khoảng cách từ điểm Ađến mp (SCD) A.
a
30
7
B.
a
30
7
C.
a
13
10
D....
Đọc tiếp
Cho hình chóp SABCD có đáy là hình thang vuông tại A, B, AD= a, AB=2a, BC=3a,SA=2a . H là trung điểm cạnh AB,SH là đường cao của hình chóp SABCD Tính khoảng cách từ điểm Ađến mp (SCD)
A. a 30 7
B. a 30 7
C. a 13 10
D. a 13 7
Đáp án B
Gọi H 1 là chân đường cao kẻ từ H đến DC. H 2 là chân đường cao kẻ từ H đến S H 1 . Khi đó ta có
H H 1 = a 2 , S H = a 3 ⇒ 1 H H 2 = 1 H H 1 2 + 1 S H 2 = 1 3 a 2 + 1 2 a 2 = 5 6 a ⇒ H H 2 = 6 5 a
⇒ d A , S C D = 30 10 a
Chọn phương án B.
Đúng 0
Bình luận (0)
9 tháng 6 2021 lúc 19:32
cho hình chóp SABCD đáy là hình thang vuông tại A,B. AB=BC=a,AD=2a. Tam giác SAD đều. (SAD) vuông góc với (ABCD). Tính thể tích SABCD
Cho hình chóp SABCD đáy là hình thang vuông tại A và B, AB = BC = a, AD = 2a, SA ⊥ (ABCD). Tìm thiết diện của hình chóp bởi mp(P) chứa AB và ⊥ (SCD)
Vì SA vuông góc (ABCD)
=>SA vuông góc CD
Gọi I là trung điểm của AD
=>AI=BC=a
mà AI//BC
nên AB=CI=a
=>AB=CI=ID
=>ΔACD vuông tại C
=>CD vuông góc AC
=>CD vuông góc (SAC)
=>(SCD) vuông góc (SAC)
Vẽ AE vuông góc SC tạiE
=>AE vuông góc (SCD)
mà \(A\in\left(P\right)\perp\left(SCD\right)\)
nên \(AE\in\left(P\right)\)
=>\(E=SC\cap\left(P\right)\)
\(E\in\left(P\right)\cap\left(SCI\right)\)
\(\left(P\right)\supset AB\)//CI thuộc (SCI)
=>(P) cắt (SCI)=Ex//AB//CI
Gọi F=Ex giao SI
=>(P) cắt (SAD) tại AJ
Gọi F=AJ giao SD
=>F=(P)giao (SD)
=>Tứ giác cần tìm là ABEF
Đúng 2
Bình luận (0)
9 tháng 6 2021 lúc 8:52
Cho hình chóp SABCD đáy là hình thang vuông tại A và B có AB=BC=a, AD=2a,(SAC) và (SAB) cùng vuông góc với đáy. Tính thể tích SABCD biết a)SB tạo với đáy là 60° b)SC tạo với đáy là 45° c)(SCD) tạo với (ABCD) là 30°
Ta có: \(S_{ABCD}=\dfrac{\left(BC+AD\right).AB}{2}=\dfrac{3}{2}a^2\)
a, \(h=SA=AB.tan60^o=a\sqrt{3}\)
\(\Rightarrow V=\dfrac{1}{3}.S_{ABCD}.h=\dfrac{1}{3}.\dfrac{3}{2}a^2.a\sqrt{3}=\dfrac{\sqrt{3}}{2}a^3\)
b, \(h=SA=AD.tan45^o=2a\)
\(\Rightarrow V=\dfrac{1}{3}.S_{ABCD}.h=\dfrac{1}{3}.\dfrac{3}{2}a^2.2a=a^3\)
c, Dễ chứng minh được SC vuông góc với CD tại C \(\Rightarrow\widehat{SCA}=30^o\)
\(\Rightarrow h=SA=AC.tan30^o=AD.sin45^o.tan30^o=\dfrac{\sqrt{6}}{3}a\)
\(\Rightarrow V=\dfrac{1}{3}.S_{ABCD}.h=\dfrac{1}{3}.\dfrac{3}{2}a^2.\dfrac{\sqrt{6}}{3}a=\dfrac{\sqrt{6}}{6}a^3\)
Đúng 1
Bình luận (0)
Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A,B Biết
A
B
a
;
B
C
a
,
A
D
3
a
,
S
A
a
2
. Khi
S
A
⊥
A
B
C
D
,
khoảng cách giữa hai đường...
Đọc tiếp
Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A,B Biết A B = a ; B C = a , A D = 3 a , S A = a 2 . Khi S A ⊥ A B C D , khoảng cách giữa hai đường thẳng S A , C D là:
A. a 5
B. a 5
C. 2 a 5
D. 3 a 5
Đáp án D
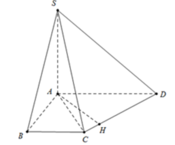
Dựng A H ⊥ C D suy ra AH là đường vuông góc cung của SA vad CD Ta có:
S A C D = 1 2 A D . d C ; A D = 1 2 .3 a . A B = 3 a 2 2 .
Lại có:
C D = A B 2 + A D − B C 2 = a 5 ⇒ A H = 2 S A C D C D = 3 a 5
Đúng 0
Bình luận (0)
1 tháng 6 2021 lúc 9:26
Cho hình chóp SABCD đáy là hình thang vuông tại A và B. AD=2a; AB=BC=a. SC tạo với đáy 1 góc 60°. Tính khoảng cách biết SA vuông góc với đáy a)SA đến BC b)SA đến CD c)AD đến SC
Cho hình chóp SABCD. có đáy ABCD là hình thang vuông tại A và D với AD = CD = a, AB = 3a . Cạnh bên SA vuông góc với mặt đáy và cạnh bên SC tạo với mặt đáy một góc 450. Tính thể tích khối chóp SABCD theo a.
anh có thể tham khảo những bài toán tương tự ở khối đa diện | Toán học phổ thông - SGK
Đúng 0
Bình luận (0)
12 tháng 5 2021 lúc 9:31
Cho hình chóp SABCD là hình thang vuông tại A và B. AD=2a, SA=a căn 3, AB=BC=a. SA vuông góc với đáy. Tính khoảng cách từ. a)A đến (SBC) b)A đến (SCD) c)BC đến (SAD)
Cho hình chóp SABCD có đáy là hình thang vuông tại A;B với BC là đáy nhỏ. Biết rằng tam giác SAB đều có cạnh là 2a và nằm trong mặt phẳng vuông góc với đáy,
S
C
a
5
và khoảng cách từ D tới mặt phẳng (SHC) là
2
a
2
(H là trung điểm của AB). Thể tích khối chóp S.ABCDlà: A.
a
3
3...
Đọc tiếp
Cho hình chóp SABCD có đáy là hình thang vuông tại A;B với BC là đáy nhỏ. Biết rằng tam giác SAB đều có cạnh là 2a và nằm trong mặt phẳng vuông góc với đáy, S C = a 5 và khoảng cách từ D tới mặt phẳng (SHC) là 2 a 2 (H là trung điểm của AB). Thể tích khối chóp S.ABCDlà:
A. a 3 3 3
B. a 3 3
C. 4 a 3 3 3
D. 4 a 3 3
Đáp án là C
ta có S A B ⊥ A B C D S A B ∩ A B C D = A B S H ⊥ A B ⇒ S H ⊥ A B C D
mà D I ⊥ C H D I ⊥ S H ⇒ D I ⊥ S H C ⇒ d D , S H C = D I = 2 a 2
ta có
Δ B H C = Δ A H E ⇒ S Δ B H C = S Δ A H E ; H E = H C
mà
S A B C D = S A H C D + S Δ B H C = S A H C D + S Δ A H E = S Δ D C E
Tam giác SAB đều nên . S H = a 3
Tam giác SHC có
H C = S C 2 − S H 2 = a 2 ⇒ E C = 2 H C = 2 a 2 .
Khi đó S A B C D = S Δ D C E = 1 2 D I . E C = 4 a 2 .
Vậy V A B C D = 1 3 S H . S A B C D = 1 3 a 3 .4 a 2 = 4 a 3 3 3 .
Đúng 0
Bình luận (0)