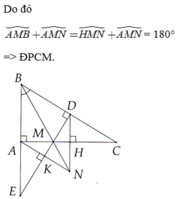
Chứng minh ba điểm B, M, K thẳng hàng

Những câu hỏi liên quan
\(Bài 3. (6đ) Cho tam giác ABC có ; AB < AC ; phân giác BE, . Lấy điểm H thuộc cạnh BC sao cho BH = BA. a) Chứng minh . b) Chứng minh BE là đường trung trực của AH. c) Đường thẳng EH cắt đường thẳng AB ở K. Chứng minh EK = EC. d) Chứng minh AH // KC. e) Gọi M là trung điểm của KC. Chứng minh ba điểm B, E, M thẳng hàng. \)
a) Bạn ghi câu a) không rõ ràng nên mình thay thế bằng ý kiến của mình nhé !
CMR : \(\Delta ABE=\Delta HBE\)
Xét \(\Delta ABE,\Delta HBE\) có :
\(BA=BH\left(gt\right)\)
\(\widehat{ABE}=\widehat{HBE}\) (BE là tia phân giác của \(\widehat{B}\) )
\(BE:chung\)
=> \(\Delta ABE=\Delta HBE\left(c.g.c\right)\)
b) Gọi \(AH\cap BE=\left\{O\right\};O\in BE\)
Xét \(\Delta ABO,\Delta HBO\) có :
\(AB=BH\left(gt\right)\)
\(\widehat{ABO}=\widehat{HBO}\) (BE là tia phân giác của \(\widehat{B}\) ; \(O\in BE\))
AO : Chung
=> \(\Delta ABO=\Delta HBO\left(c.g.c\right)\)
=> \(\widehat{BOA}=\widehat{BOH}\) (2 góc tương ứng)
Mà : \(\widehat{BOA}+\widehat{BOH}=180^o\left(Kềbù\right)\)
=> \(\widehat{BOA}=\widehat{BOH}=\dfrac{180^o}{2}=90^o\)
=> \(BO\perp AH\)
Hay : \(BE\perp AH\)
c) Ta chứng minh được : \(\Delta BKE=\Delta BCE\)
Suy ra : \(EK=EC\) (2 cạnh tương ứng)
d) Xét \(\Delta ABC\) có :
BE là tia phân giác của \(\widehat{ABC}\) (1)
Xét \(\Delta KEM,\Delta CEM\) có :
\(EK=EC\left(cmt\right)\)
\(EM:chung\)
\(KM=CM\) (M là trung điểm của KC)
=> \(\Delta KEM=\Delta CEM\left(c.c.c\right)\)
=> \(\widehat{MEK}=\widehat{MEC}\) (2 góc tương ứng)
=> EM là tia phân giác của \(\widehat{KEC}\) (2)
Từ (1) và (2) => \(BE\equiv ME\)
=> B, E, M thẳng hàng
=> đpcm.
Đúng 0
Bình luận (1)
Cho hình vẽ Chứng minh ba điểm B K C thẳng hàng
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC tại điểm M. Kẻ
M
D
⊥
B
C
(
D
∈
B
C
)
.
a) Chứng minh BA BD.b) Gọi E là giao điểm của hai đường thẳng DM và BA. Chứng minh
∆
A
B
C
∆
D
B
E
.
c) Kẻ
D
H
⊥
M
C
(
H
∈
M
C...
Đọc tiếp
Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC tại điểm M. Kẻ M D ⊥ B C ( D ∈ B C ) .
a) Chứng minh BA = BD.
b) Gọi E là giao điểm của hai đường thẳng DM và BA. Chứng minh ∆ A B C = ∆ D B E .
c) Kẻ D H ⊥ M C ( H ∈ M C ) và A K ⊥ M E ( K ∈ M E ) . Gọi N là giao điểm của hai tia DH và AK. Chứng minh MN là tia phân giác góc HMK.
d) Chứng minh ba điểm B, M, N thẳng hàng.
Cho DABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm M sao cho
BM = BA. Qua M kẻ đường thẳng vuông góc với BC, cắt AC tại I.
a. Chứng minh AI = IM
b. Tia MI cắt tia BA tại điểm N. Chứng minh DNBC cân.
c. Gọi K là trung điểm của NC. Chứng minh B, I, K thẳng hàng
d. Trên tia IC lấy điểm P sao cho IP = IA. Chứng minh DMAP là tam giác vuông.
Cho tam giác ABC có AB = AC, lấy M là trung điểm của BC.
a) Chứng minh ∆ABM = ∆ACM
b) Kẻ ME ⊥ AB tại Em kẻ MF ⊥ AC tại F. Chứng minh AE = AF.
c) Gọi K là trung điểm của EF. Chứng minh ba điểm A, K, M thẳng hàng
d) Từ C kẻ đường thẳng song song với AM cắt tia BA tại D. Chứng minh A là trung điểm của BD.
Cho hình dưới (hình 65a). Chứng minh rằng ba điểm B, K, C thẳng hàng
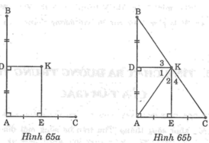
Nối KA, KB, KC (hình 65b).
Vì KD là đường trung trực của AB nên:
KA = KB (tính chất đường trung trực)
Suy ra: ΔKAB cân tại K
Do đó KD là đường phân giác của ∠(AKB)
Suy ra: ∠K1 = ∠K3 ⇒ ∠(AKB) = 2 ∠K1 (1)
Vì KE là đường trung trực của AC nên:
KA = KC (tính chất đường trung trực)
Do đó, tam giác AKC cân tại K. Suy ra KE là đường phân giác của ∠(AKC)
Suy ra: ∠K2 = ∠K4 ⇒ ∠(AKC) = 2 ∠K2 (2)
Ta có: KD ⊥ AB (gt) và AC ⊥ AB (gt)
Suy ra: KD // AC (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song nhau)
Lại có: KE ⊥ AC (gt)
Suy ra: KE ⊥ KD (quan hệ giữa tính vuông góc và tính song song)
Hay: ∠(DKE) = 90o⇒ ∠K1 +∠K2 = 90o
Từ (1) và (2) suy ra: ∠(AKB) + ∠(AKC) = 2∠K1 + 2∠K2
= 2.( ∠K1 +∠K2 ) = 2.90o = 180o.
Vậy B, K, C thẳng hàng.
Đúng 0
Bình luận (0)
: Cho tam giác nhọn ABC có M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao choMD MAChứng minh AMB DMC. b) Chứng minh AB // CD. c) Từ M vẽ MH AB (HAB), MK CD (KCD). Chứng minh ba điểm H, M, K thẳng hàng
Đọc tiếp
: Cho tam giác nhọn ABC có M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho
MD = MA
Chứng minh ![]() AMB =
AMB = ![]() DMC.
DMC.
b) Chứng minh AB // CD.
c) Từ M vẽ MH ![]() AB (H
AB (H![]() AB), MK
AB), MK ![]() CD (K
CD (K![]() CD). Chứng minh ba điểm H, M, K thẳng hàng
CD). Chứng minh ba điểm H, M, K thẳng hàng
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB//CD
Đúng 1
Bình luận (0)
Cho tam giác ABC có góc A=90 độ. Gọi M và N lần lượt là trung điểm của AC và AB. Trên tia đối của MB lấy K sao cho MK=MB. Trên tia đối của MC lấy I sao cho NI=NC.
a) Tính góc ACK.
b) Chứng minh: IB//AC; AK//BC.
c) Chứng minh ba điểm I, A, K thẳng hàng.
d) Gọi P là trung điểm của CK. Chứng minh ba điểm P, M, N thẳng hàng.
xét tam giác ABM và tam giác CMK
AM = MC ( M là trung điểm của AC)
BM=MK
góc AMB =góc CMK
=> tam giác ABM và tam giác CMK( c.g.c)
=>goc BAC = goc ACK ( hai canh tuong ung )
ma goc BAC = 900
=> góc ACK= 900
Đúng 0
Bình luận (0)
mình đã trả lời hết các câu rồi nhưng mình ko may nhấn vào trang khác trên màn hình nên khi trả về thì không còn nên mình chỉ làm câu a cho mình xin lỗi nhưng nếu bạn còn cần thì mình giải ngày cho .cảm ơn bạn
Đúng 0
Bình luận (0)
Ai giải đc xin giải nhanh cho. đúng thì mik k
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm K sao cho BK=BA. Gọi M là trung điểm của đoạn thẳng AK. a) Chứng minh: ∆AMB=∆KMB b) Đường thẳng BM cắt đường thẳng AC tại D. Chứng minh: DK vuông góc với BC. c) Trên tia đối của tia AB lấy điểm H sao cho ah=kc chứng minhh d k thẳng hàng