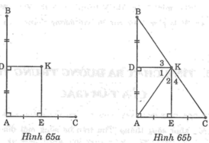
Nối KA, KB, KC (hình 65b).
Vì KD là đường trung trực của AB nên:
KA = KB (tính chất đường trung trực)
Suy ra: ΔKAB cân tại K
Do đó KD là đường phân giác của ∠(AKB)
Suy ra: ∠K1 = ∠K3 ⇒ ∠(AKB) = 2 ∠K1 (1)
Vì KE là đường trung trực của AC nên:
KA = KC (tính chất đường trung trực)
Do đó, tam giác AKC cân tại K. Suy ra KE là đường phân giác của ∠(AKC)
Suy ra: ∠K2 = ∠K4 ⇒ ∠(AKC) = 2 ∠K2 (2)
Ta có: KD ⊥ AB (gt) và AC ⊥ AB (gt)
Suy ra: KD // AC (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song nhau)
Lại có: KE ⊥ AC (gt)
Suy ra: KE ⊥ KD (quan hệ giữa tính vuông góc và tính song song)
Hay: ∠(DKE) = 90o⇒ ∠K1 +∠K2 = 90o
Từ (1) và (2) suy ra: ∠(AKB) + ∠(AKC) = 2∠K1 + 2∠K2
= 2.( ∠K1 +∠K2 ) = 2.90o = 180o.
Vậy B, K, C thẳng hàng.